Решение задачи способом замены плоскостей проекций.
Как отмечалось выше, для определения расстояния от заданной точки до плоскости (высоты пирамиды) необходимо из этой точки опустить перпендикуляр на плоскость, найти основание перпендикуляра и определить истинную величину отрезка. Задача решается просто, если плоскости основания пирамиды — ΔАВС задать проецирующее положение.
1. Построим в плоскости треугольника АВС горизонталь и введем новую фронтальную плоскость π4 перпендикулярно к данной горизонтали:
На чертеже ось х1 перпендикулярна горизонтальной проекции горизонтали h1 / : х1 ^ h1 / ; (рис.10.1)
2.Строим новую фронтальную проекцию треугольника — А1 // В1 // С1 // .
[S // Sx // ] 


[C // Cx // ] 
По отношению к p4 плоскость треугольника занимает проецирующее положение(рис.10.2).
3. Из точки S1опускаем перпендикуляр на плоскость DА1В1С1, находим его основание, как точку пересечения перпендикуляра с плоскостью:
S1K1 

На чертеже: S1«K1» 
Отрезок [S1«K1«]определяет натуральную величину высоты пирамиды. Измеряем его и указываем размер на чертеже.
Точку К необходимо вернуть в исходное положение, зная что S1 / K / ¤¤ х (рис.10.3);
Задача 3. Определить натуральную величину основания пирамиды — DАВС.
Решение способом плоскопараллельного перемещения.
Для того чтобы определить натуральную величину основания пирамиды-DABC, который является плоскостью общего положения, необходимо преобразовать его в плоскость уровня.
Для решения задачи необходимо выполнить два преобразования:
1) Преобразовать плоскость треугольника – плоскость общего положения в проецирующую плоскость.
2) Преобразовать проецирующую плоскость в плоскость уровня,
переместив ΔA1B1C1 плоскопараллельным движением относительно пл. p2 в новое положение, параллельное пл. p1, тогда на эту плоскость он спроецируется без искажения.
a1(A1B1C1) 
1. Перемещаем треугольник АВС параллельно одной из плоскостей проекций так, чтобы после преобразования он занял проецирующее положение ( см. задачу №1).
2.Располагаем вырожденную фронтальную проекцию DA2B2C2 –отрезок [A2 // B2 // C2 // ]параллельно оси х:
При этом не изменится величина его фронтальной проекции:
[A2 // B2 // C2 // ] 
3. Горизонтальные проекции вершин А1 / , В1 / , . перемещаются в новое положение А2 / ,В2 / , . по прямым параллельным оси х. По линиям связи строим горизонтальную проекцию DA2B2C2 (ΔA2 / B2 C2 / ), которая конгруэнтна основанию пирамиды: [DA2 / B2 / C2 / ] 
Источник
Примеры решения метрических задач



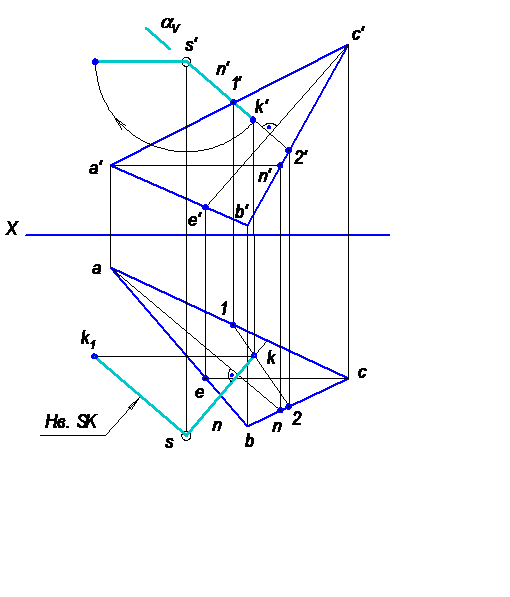
Задача 1. Определить высоту пирамиды SABC (SK).
Высота пирамиды определяется длиной перпендикуляра, опущенного из точки S на плоскость основания АВС – SK (рисунок 6.17).
Рисунок 6.17− Пример решения задачи 1
1. Опустить перпендикуляр n из точки S на основание АВС.
2. Построить основание К перпендикуляра n (точка встречи перпендикуляра с плоскостью АВС).
3. Определить натуральную величину отрезка SK, выражающего высоту пирамиды.
1. Перпендикуляр n из точки S на основание АВС пирамиды проводим без преобразования проекций. В этом случае построение проекций перпендикуляра основано на теореме о перпендикулярности прямой и плоскости, согласно которой проекции перпендикуляра к плоскости перпендикулярны к одноименным проекциям фронтали и горизонтали этой плоскости.
Поэтому на первом этапе решения задачи:
а) проводим в плоскости АВС горизонталь AN и располагаем горизонтальную проекцию перпендикуляра n перпендикулярно горизонтальной проекции горизонтали:
б) проводим в плоскости основания АВС фронталь СЕ и располагаем фронтальную проекцию перпендикуляра n перпендикулярно фронтальной проекции фронтали:
2. Основание К перпендикуляра n находим с помощью вспомогательной плоскости a:
а) заключаем перпендикуляр n во фронтально проецирующую плоскость a: nÎa; a ^V;
б) определяем линию пересечения L плоскости a и основания АВС: l = a Ç D ABC; l = 1 È 2;
в) находим точку пересечения К перпендикуляра n и основания АВС: К = n Ç D ABC.
3. Натуральную величину отрезка SK, выражающего высоту пирамиды, определяем методом вращения вокруг осей, перпендикулярных к плоскостям проекций. Для этого поворачиваем отрезок SK в положение, параллельное плоскости Н. Новая горизонтальная проекция sk1 отрезка представляет его натуральную величину.
Задача 2.Определить угол, образованный гранью SAB и основанием АВС пирамиды (рисунок 6.18).
Угол между двумя плоскостями определяется линейным углом, полученным при сечении данных плоскостей третьей плоскостью, перпендикулярной к двум заданным. Поскольку таким путем задача решается сложно, прибегаем к одному из способов преобразования ортогональных проекций. Например, к способу замены плоскостей проекций. Решение задачи показано на рисунке 6.18.
Рисунок 6.18 − Пример решения задачи 2
1. Линию пересечения заданных плоскостей SAB и АВС – ребро АВ – из прямой общего положения преобразуем в проецирующую прямую.
2. Определить проекции плоскостей SAB и АВС в новой системе плоскостей ортогональных проекций.
3. Определить угол между гранью SAB и основанием АВС как угол между пересекающимися прямыми, в которые эти плоскости проецируются в результате преобразования.
1. Сначала заменяем плоскость V на новую V1, располагаем ее параллельно ребру АВ (на эпюре Х1 ½½ab) и строим новую фронтальную проекцию пирамиды. Затем заменяем плоскость Н на новую Н1, располагая последнюю перпендикулярно ребру АВ (на эпюре Х2 ^ a1‘b1‘) и строим новую горизонтальную проекцию ребра АВ.
2. Строим новую горизонтальную проекцию плоскостей SAB и АВС. Они изобразятся в виде пересекающихся прямых (рисунок 6.18).
3. Определяем угол j 0 , выражающий угол между гранью SAB и основанием АВС пирамиды.
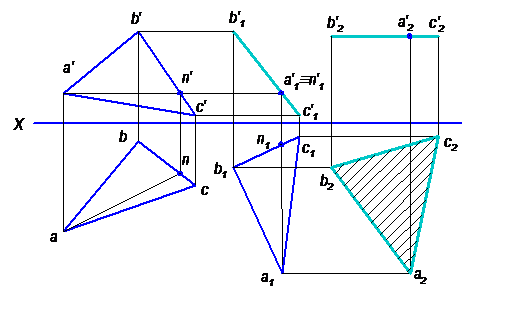
Задача № 3.Определить натуральную величину основания АВС пирамиды.
Для определения натуральной величины и формы плоской фигуры необходимо расположить ее параллельно одной из плоскостей проекций. Для этого воспользуемся способом плоскопараллельного перемещения. Решение задачи показано на рисунке 6.19.
1. Преобразовать плоскость АВС общего положения в проецирующую.
2. Преобразовать плоскость АВС в плоскость уровня и определить ее натуральную величину и форму.
1. Проводим в плоскости АВС горизонталь AN. Перемещаем горизонталь AN параллельно плоскости Н и поворачиваем ее в новом положении перпендикулярно плоскости V (на эпюре a1n1 ^ X). Строим новую горизонтальную проекцию a1b1c1 конгруэнтную авс и новую фронтальную проекцию в виде прямой b1‘c1‘.
Рисунок 6.19 − Пример решения задачи 3
Перемещаем плоскость АВС параллельно плоскости V в положение, параллельное плоскости Н (на эпюре b2‘c2‘ || X), и находим новую горизонтальную проекцию a2b2c2, представляющую натуральную величину и форму основания АВС.
Контрольные вопросы по начертательной геометрии
К теме 1. Центральные и параллельные проекции.
1.1. Какие известны вам основные методы проецирования геометрических форм на плоскости?
1.2. Сформулируйте основные свойства параллельного проецирования.
1.3. Что называют координатами точки пространства в декартовой системе координат?
К теме 2. Точка. Прямая. Плоскость на эпюре Монжа.
2.1. Постройте проекции точек, расположенных в различных углах пространства.
2.2. Что называют постоянной прямой чертежа? Как с помощью постоянной прямой чертежа построить третью проекцию точки.
2.3. Какие прямые называют линиями уровня ?
2.4. Какие прямые называют проецирующими прямыми линиями?
2.5. Приведите определение внутреннего и внешнего деления отрезка прямой.
2.6. Что называют следом прямой линии? постройте следы прямых частного положения.
2.7. Укажите правило построения следов прямой линии.
2.8. Как изображаются на чертеже пересекающиеся, параллельные и скрещивающиеся прямые линии?
2.9. Покажите способы задания плоскости общего положения и проецирующих плоскостей.
2.10 Как строят прямые линии и точки в плоскости?
2.11. Покажите способы построения горизонтали, фронтали и линии наибольшего наклона плоскостей общего положения и проецирующих плоскостей.
К теме 3. Позиционные и метрические задачи.
3.1. Покажите на примерах, как определяют точки пересечения проецирующих плоскостей прямыми линиями, линии пересечения проецирующих плоскостей плоскостями общего положения и проецирующими плоскостями.
3.2. Изобразите схему и укажите последовательность решения задачи на построение точки пересечения прямой с плоскостью общего положения.
3.3. Как определяют видимость элементов геометрических образов относите плоскостей проекций?
3.4. Изобразите схему и укажите последовательность построения линии пересечения двух плоскостей.
3.5. Изобразите схему и приведите примеры построений прямых линий, параллельных и перпендикулярных плоскостям.
3.6. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.
3.7. Сформулируйте условие перпендикулярности двух прямых общего положения. Изобразите схему.
3.8. Как определяются на чертеже расстояния от точки до проецирующей плоскости и плоскости общего положения?
Тема № 4. Способы преобразования.
4.1. В чем состоит принцип преобразования чертежа способом замены плоскостей проекций?
4.2. Какова схема решения задачи по определению натуральной величины отсека произвольно расположенной плоскости способом замены плоскостей проекций?
4.3. В чем состоит принцип преобразования чертежа способом вращения вокруг проецирующих прямых?
4.4. Какую прямую принимают за ось вращения при переводе отсека плоскости из общего положения в горизонтально — проецирующую плоскость?
4.5. Можно ли считать плоскопараллельное перемещение вращением вокруг не выявленных осей и почему?
4.6. Укажите последовательность приемов определения натуральной величины отсека плоскости способом плоскопараллельного перемещения.
К теме 5. Пересечение поверхностей плоскостью и прямой линией.
5.1. Каковы основные способы задания поверхностей?
5.2. Укажите общую схему определения точек линии пересечения поверхностей плоскостью.
5.3. Укажите последовательность графических построений при определении точек пересечения прямой с поверхностью.
5.4. Укажите условия, при которых в сечении конуса вращения плоскостью получаются окружность, эллипс, гипербола, парабола, пересекающиеся прямые.
К теме 6. Взаимное пересечение поверхностей.
6.1. Изобразите общую схему построения линий пересечения
6.2. Назовите основные способы построения линий пересечения поверхностей.
6.3. Опишите способы секущих плоскостей и сферических посредников при определении линии пересечения поверхностей.
6.4. Какое пересечение поверхностей называют полным и неполным?
6.5. В какой последовательности соединяются точки искомой линии пересечения поверхностей и как определяется ее видимость в проекциях?
6.6. Какие точки линии пересечения поверхностей называют главными (опорными)?
К теме 7. Развертка поверхностей.
7.1. Что называют разверткой поверхностей?
7.2. Какие поверхности называют развертывающимися и какие не развертывающимися?
7.3. Укажите основные свойства разверток.
7.4. Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.
К теме 8. Аксонометрические проекции.
8.1. Какие проекции называют аксонометрическими?
8.2. Что называют коэффициентом искажения?
8.3. Сформулируйте основную теорему аксонометрии – теорему Польке.
8.4. Что представляет собой треугольник следов?
8.5. Укажите коэффициенты искажений по направлениям осей в прямоугольной изометрии, в диметрии.
8.6. Укажите направления и величины осей эллипсов как изометрических и диметрических проекций окружностей, вписанных в квадрат граней куба, ребра которого параллельны координатным осям.
Источник