Дана полоска 1х15 сколькими способами ее можно закрасить две соседние клетки

Дана полоска 1х15 сколькими способами ее можно закрасить две соседние клетки

а) Поставим сначала чёрную ладью. Это можно сделать 8 · 8 = 64 способами. Чтобы белая ладья её не била, надо поставить её в другие горизонталь и вертикаль, то есть свободных для неё горизонталей будет 8 — 1 = 7, и вертикалей тоже 8 — 1 = 7. То есть, поставить белую ладью при уже поставленной чёрной можно 7 · 7 = 49 способами. Так как на каждый из 64 способов поставить чёрную ладью будет 49 способов поставить белую, то всего способов поставить обе будет 64 · 49 = 3136.

б) Поставим сначала чёрного короля. Сколько способов тогда останется для постановки белого? Рассмотрим разные случаи:

Если чёрный король стоит в углу доски, то белого нельзя ставить на 4 клетки, то есть можно поставить на одну из 8·8 — 4 = 60 клеток. Углов в доске 4, то есть таких случаев, когда чёрный король стоит в углу, а белый его не бьёт, 4 · 60 = 240.

Дальше, если чёрный король стоит с краю доски (не в углу), то белого нельзя ставить на 6 клеток, то есть можно ставить на 64 — 6 = 58 клеток. На каждой из 4 сторон доски есть 8 — 2 = 6 клеток, где чёрный король будет стоять с краю, но не в углу, то есть всего таких вариантов растановки обоих королей будет 4 · 6 · 58 = 1392.

Наконец, если чёрный король стоит на внутренней клетке доски (они образуют квадрат со стороной 8 — 2 = 6, поэтому внутренних клеток будет 6 · 6 = 36), то белого можно поставить на одну из 64 — 9 = 55 клеток. Всего вариантов расстановки, где чёрный король стоит на внутренней клетке, будет 36 · 55 = 1980.

Итак, всего подходящих вариантов будет 240 + 1392 + 1980 = (200 + 40) + (1400 — 8) + (2000 — 20) = 1600 + 2000 + (40 — 20 — 8) = 3600 + 12 = 3612

Источник

Дана полоска 1х15 сколькими способами ее можно закрасить две соседние клетки

а) Обозначим искомую сумму S:
S = 1 + 2 + 3 + . + 50
Теперь запишем ту же сумму в обратном порядке:
S = 50 + 49 + 48 + . + 1
Напишем эти формулы одну под другой и «сложим в столбик», складывая слагаемые, написанные друг под другом:
S = 1 + 2 + 3 + . + 50
S = 50 + 49 + 48 + . + 1
2S = 51 + 51 + 51 + . + 51
В последней сумме 50 слагаемых (как и в исходной сумме), поэтому 2S = 51·50, откуда S = 51 · 50 : 2 = 1275.

б) Решаем аналогично пункту а:
S = 10 + 11 + 12 + . + 99
S = 99 + 98 + 97 + . + 10
2S = 109 + 109 + 109 + . + 109
В последней сумме 90 слагаемых (именно столько существует двузначных чисел и именно столько слагаемых в исходной сумме), поэтому 2S = 109·90, откуда S = 109 · 90 : 2 = 4905.

в) Решаем аналогично пунктам а и б:
S = 1000 + 1001 + 1002 + . + 9999
S = 9999 + 9998 + 9997 + . + 1000
2S = 1099 + 1099 + 1099 + . + 1099
В последней сумме 9000 слагаемых (именно столько существует четырёхзначных чисел и именно столько слагаемых в исходной сумме), поэтому 2S = 1099·9000, откуда S = 1099 · 9000 : 2 = 49495500.

Будем решать эту задачу по аналогии с задачей 1.

а) Обозначим искомую сумму S:
S = 1 + 3 + 5 + . + 99
S = 99 + 97 + 95 + . + 1
2S = 100 + 100 + 100 + . + 100
В последней сумме 50 слагаемых (как и в исходной сумме: среди 100 чисел от 1 до 100 ровно половина нечётных), поэтому 2S = 100·50, откуда S = 100 · 50 : 2 = 2500.

б) Решаем аналогично пункту а:
S = 3 + 6 + 9 + . + 150
S = 150 + 147 + 144 + . + 3
2S = 153 + 153 + 153 + . + 153
В последней сумме 150 : 3 = 50 слагаемых (как и в исходной сумме: среди 150 чисел от 1 до 150 ровно треть делится на 3), поэтому 2S = 153·50, откуда S = 153 · 50 : 2 = 3825.

в) Решаем аналогично пунктам а и б:
S = 1 + 7 + 13 + . + 79
S = 79 + 73 + 67 + . + 1
2S = 80 + 80 + 80 + . + 80
В последней сумме 14 слагаемых (как и в исходной сумме: неполные частные от деления этих чисел на 6 равны, соответственно, 0, 1, 2, . 13), поэтому 2S = 80·14, откуда S = 80 · 14 : 2 = 560.
Обратите внимание: поскольку 1 = 6·0 + 1, число 1 тоже делится на 6 с остатком 1 (и неполным частным 0).

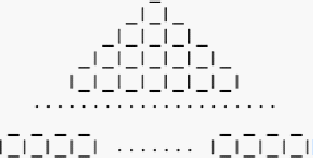
Число клеток в k -м ряду фигуры равно k -му нечётному числу. Значит, площадь такой фигуры из n рядов равна сумме первых n нечётных чисел.

а) 1 + 3 + 5 + 7 + 9 = 25.

б) Двадцать пятое нечётное число — это число 49. Аналогично задаче 1 вычислим, что 1 + 3 + 5 + . + 49 = (1 + 49) · 25 : 2 = 25 2 = 625.

в) Заметим, что число клеток в такой фигуре всегда равно квадрату числа рядов. Это легче всего заметить геометрически (см. рисунок ниже).

Можно получить тот же результат и иначе. Заметим, что k -е нечётное число равно (2 k −1) (проверьте!). Таким образом, если фигура состоит из n рядов, число клеток в ней равно сумме нечётных чисел от 1 до (2 n −1). Вычислим эту сумму:
S = 1 + 3 + 5 + . + (2 n −1)
S = (2 n −1) + (2 n −3) + (2 n −5) + . + 1
2S = 2 n + 2 n + 2 n + . 2 n = 2 n · n
S = n · n = n 2 .

final: Последовательность Фибоначчи — такая последовательность натуральных чисел, в которой первые два числа — единицы, а каждое следующее число равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, . .

а) Очевидно, что полоску 2×1 можно разрезать на доминошки одник способом, а полоску 2×2 — двумя. Далее, если от полоски 2×3 вначале отрезать одну вертикальную доминошку, останется полоска 2×2, которую можно разрезать одним из двух способов (как мы отметили выше). Если же от полоски 2×3 вначале отрезать две горизонтальные доминошки, останется прямоугольник 2×1, который можно разрезать одним способом. Итого полоску 2×3 можно разрезать 2 + 1 = 3 способами.

б) Аналогичным образом поступим с полоской 2×4. Либо мы сначала отрезаем одну вертикальную доминошку, и остаётся прямоугольник 2×3, который можно разрезать пятью способами, либо мы сначала отрезаем две горизонтальные доминошки, и остаётся прямоугольник 2×2, который можно разрезать тремя способами. Итого полоску 2×4 можно разрезать на доминошки 5 + 3 = 8 способами.

в)Рассуждая таким же образом, как в пунктах а и б, посчитаем, что полоску 2×5 можно разрезать 8 + 5 = 13 способами.

Докажем, что (число способов разрезать полоску 2×2013) = (число способов разрезать полоску 2×2012) + (число способов разрезать полоску 2×2011). В самом деле, если сначала отрезать от полоски 2×2013 одну вертикальную доминошку, останется полоска 2×2012, которую ещё надо разрезать; если же сначала отрезать две горизонтальные доминошки, останется разрезать полоску 2×2011. А из этого следует, что Даша и Таня в результате получили одно и то же число.

Вычислим сумму первых n подряд идущих натуральных чисел:
S = 1 + 2 + 3 + . + n
S = n + ( n −1) + ( n −2) + . + 1
2S = ( n +1) + ( n +1) + ( n +1) + . ( n +1) = n ·( n +1)
S = n ·( n +1) : 2.

Чтобы это число оканчивалось цифрой 7, вдвое большее число n ·( n +1) должно оканчиваться цифрой 4 (так как последняя цифра числа 2·7 = 14 равна 4). Последняя цифра произведения двух чисел равна последней цифре произведения их последних цифр (вспомните правило умножения в столбик). Пользуясь этим соображением, составим таблицу:

Последняя цифра числа n	Последняя цифра числа ( n +1)	Последняя цифра числа n ·( n +1)
0	1	0
1	2	2
2	3	6
3	4	2
4	5	0
5	6	0
6	7	2
7	8	6
8	9	2
9	0	0

В последнем столбце этой таблицы нигде не встречается цифра 4. Значит, число n ·( n +1) ни при каких n не может оканчиваться цифрой 4, а число n ·( n +1) : 2 ни при каких n не может оканчиваться цифрой 7.

а) Обозначим через а_n число способов подняться на лестницу из n ступенек, соблюдая условия задачи. Очевидно, a ₁ = 1, a ₂ = 2. Пусть Петя запрыгивает на лестницу из n > 2 ступенек. Если первый прыжок был на две ступеньки, то ему осталось запрыгнуть на ( n − 2) ступеньки, и число способов закончить подъем равно a_{n −2}. Если же первый прыжок был на одну ступеньку, то число способов закончить подъем равно a_{n −1}. Значит, a_n = a_{n −1} + a_{n −2}. Поэтому числа a_n образуют последовательность Фибоначчи: a ₃ = 3, a ₄ = 5, a ₅ = 8, a ₆ = 13, a ₇ = 21, a ₈ = 34, a ₉ = 55, a ₁₀ = 89.

б) Каждую из 9 ступенек (кроме последней) Петя может либо перепрыгнуть, либо не перепрыгнуть независимо от того, на каких из верхних ступенек он останавливался. Поэтому количество способов спуститься по лестнице равно 2 9 = 512.

Источник

комбинаторика — Дана полоска 1 × 10

Добрый вечер! Помогите решить задачу Дана полоска 1 × 10. В клетки записываются числа 1, 2, . . . , 10 по сле- дующему правилу: сначала в какую-нибудь клетку пишут число 1, затем число 2 записывают в соседнюю клетку, затем число 3 — в одну из соседних с уже занятыми, и так далее. Сколькими способами это можно сделать? Спасибо

задан 2 Апр ’17 19:03

al1965
362 ● 1 ● 22
52&#037 принятых

1 ответ

Решим задачу для общего случая, когда полоска состоит из n клеток. Докажем по индукции, что способов имеется 2^. База индукции очевидна. Покажем, что число способов каждый раз удваивается. Когда вписано несколько первых чисел, они образуют «сплошной» ряд без пробелов. Отсюда следует, что последнее число n вписывается в одну из двух крайних клеток. Это даёт два разных типа заполнения при n > 1. Ясно, что заполнений, у которых число n занимает первую позицию, столько же, сколько способов заполнить полоску длины n-1 числами от 1 до n-1. Столько же способов заполнения имеется, если число n занимает последнюю позицию. Поэтому при переходе от n-1 к n число способов заполнения становится вдвое больше.

Можно всё заполнять не с начала, а с конца, и тогда ясно, что очередное число надо вписывать в одну из крайних свободных клеток, и на всех шагах, кроме одного, у нас есть 2 способа выбора.

Эта задача, по-моему, на форуме уже была, но ссылку я не нашёл, и решения тоже не помнил.

Источник

Разработка занятия на тему «Олимпиадная математика. Инварианты.»

Инварианты

В некоторых задачах по математике дается набор преобразований исходного объекта и спрашивается: можно ли, используя эти преобразования, получить из одного состояния объекта другое? Перебором вариантов часто легко убедиться в правильности ответа “нельзя”, однако обосновать этот ответ бывает трудно. Методом, позволяющим во многих случаях решать доказательную часть таких задач, является метод инвариант.

Инвариантом называется нечто, не меняющееся в преобразованиях, например, число, набор чисел, четность какого – либо числа и другое. Если значение инварианта в двух состояниях объекта различно, то одно из них нельзя получить из другого. Придумать инвариант должен ученик, самостоятельно решающий задачу; обычно это вызывает у него затруднения. В качестве инварианта чаще всего рассматриваются четность (нечетность) чисел и остаток от деления. Причем применение четности – одна из наиболее встречающихся идей при решении олимпиадных задач.

Вспомним определения четного и нечетного числа. Особое внимание надо уделить абстрактному понятию четности, объяснить, что такое “разная четность”. Например, число х + 2 имеет ту же четность, что и число х (или оба четные, или оба нечетные), а при прибавлении единицы четность меняется. Применение идеи четности и нечетности основано на двух важных утверждениях (леммах):

Лемма 1. Четность суммы нескольких целых чисел совпадает с четностью количества нечетных слагаемых.

Пример1. Число 1 +2 + 3 + … + 10 – нечетное, так как в сумме 5 нечетных слагаемых.

Пример 2. Число 5 + 7 + 9 + 11 +13 + 15 – четное, так как в сумме 6 нечетных слагаемых.

Лемма 2. Знак произведения нескольких (отличных от 0) чисел определяется четностью количества отрицательных сомножителей.

Пример 3 . Число (-1) *(-2) *(-3) *(-4) положительно, так как в произведении четное число отрицательных сомножителей.
Пример 4. Число (-1) *2 * (-3) * (-4) отрицательно, так как в произведении нечетное число отрицательных сомножителей.

Задача 1 . На листе бумаги написано число 11. Шестнадцать учеников передают листок друг другу, и каждый прибавляет к числу или отнимает от него единицу – как хочет. Может ли в результате получиться число 0?

Нужно предложить выполнить эту операцию учащимся (результат каждого хода записывается на доске), заметить закономерность: после каждого хода характер четности меняется: после первого ученика число становится четным, после второго нечетным; после третьего — четным; после четвертого – нечетным. Тогда после шестнадцатого число будет нечетным. Поэтому нуль в конце получиться не может.

Задача 2. На доске написано 15 чисел: 8 нулей и 7 единиц. Вам предлагается 14 раз подряд выполнить такую операцию: зачеркиваем любые два числа, и если они одинаковые, то дописываем к оставшимся числам нуль, а если разные, то единицу. Какое число останется на доске?

0 0 0 0 0 0 0 0 1 1 1 1 1 1 1

1)Если вычеркиваем два нуля, то дописываем нуль, тогда «0»-7,

«1»-7.Осталось 14 чисел. Сумма -нечетное.

2)Если вычеркиваем две единицы, то дописываем нуль, тогда «0»-9, «1»-5. Сумма -нечетное.

3)Если нуль и единицу, то дописываем единицу, тогда «0»-7,

После выполнения данной операции на доске получается на одно число меньше.

—сумма оставшихся чисел все время число нечетное.

Значит, после 14 раз указанной операции на доске останется одно и нечетное число, а это-1!

Задача 3. В таблице, где имеются 15 чисел (-1), можно производить следующую операцию: одновременно изменить знак двух (не более, не меньше) чисел в таблице. Можно ли, применяя эту операцию конечное число раз, получить таблицу, состоящую из (+ 1)?

Решение. Ответ: нельзя. Так как число чисел в таблице нечетно, а после каждой операции число чисел (+ 1) в таблице четно. На языке инвариантов это означает: инвариантом таблицы относительно введенной операции является произведение всех чисел в таблице. В начальный момент это произведение равно ( — 1), а нам нужно получить таблицу, инвариант которой равен ( + 1).

Задача 4. Квадрат 5х5 заполнен числами так, что произведение чисел в каждой строке отрицательно. Доказать, что найдется

столбец, в котором произведение чисел также отрицательно.

Найдем произведение всех чисел. Оно отрицательно.

Произведение всех чисел равно произведению чисел в столбцах.

А так как произведение всех чисел отрицательно, то оно должно быть отрицательно в пяти, трех или хотя бы в одном столбце.

Что и требовалось доказать!

Задача 5. 16 корзин расположили по кругу. Можно ли в них разложить 55 арбузов так, чтобы количество арбузов в любых двух соседних корзинах отличалось на 1?

Т.к количество арбузов в любых двух соседних корзинах отличается на 1, то рассмотрим сумму: ч + н + ч +…+ н =55

Или н + ч + н +…+ ч = 55.

И т.к. это будет сумма 16 слагаемых и нечетных слагаемых в ней – 8(четное),то сумма должна быть четным числом!

Значит, разложить 55 арбузов нельзя!

Задачи для самостоятельного решения(6-7 классы):

На вешалке висят 20 платков. 17 девочек по очереди подходят к вешалке, и каждая либо снимает, либо вешает ровно один платок. Может ли после ухода девочек на вешалке остаться 10 платков?

Решение: После подхода первой девочки количество оставшихся платков либо 19, либо 21 (нечетное количество); после подхода второй девочки – либо 18, либо 20, либо 22 (четное количество); после подхода третьей девочки – либо 17, либо 21, либо 23, либо 19 (нечетное количество). После подхода 17 девочки остается нечетное количество платков. Получается противоречие. Значит, 10 платков остаться не может.

Разменный автомат меняет одну монету на пять других. Можно ли с его помощью разменять металлический рубль на 26 монет?

Решение: Нельзя. Проследите за остатками по модулю 4.

На столе 6 стаканов, Из них 5 стоят правильно, а один перевернут вверх дном. Разрешается переворачивать одновременно 4 любых стакана. Можно ли все стаканы поставить правильно?

Решение. Нет, так как в любом случае перевернутых вверх дном стаканов будет числом нечетным.

В марсианском алфавите есть две буквы — У и Ы, причем если из любого слова выкинуть стоящие рядом буквы УЫ, то смысл слова не изменится. Точно также смысл не изменится при добавлении в любое место слова буквосочетания ЫУ или УУЫЫ. Верно ли, что слова ЫУЫУЫ и УЫУЫУ имеют одинаковый смысл?

Решение: Обратите внимание, что при любой разрешенной нам операции добавления или выкидывания куска слова количества букв У и Ы в этом куске равны. Это означает, что разность между числом букв У и букв Ы в слове не изменяется. Проследите это на примере

Ы -> ЫЫУ -> ЫУУЫЫЫУ -> ЫУЫЫУ

Во всех этих словах букв Ы на одну больше, чем букв У. Вернемся к решению. В слове ЫУЫУЫ разность равна (-1), а в слове УЫУЫУ равна 1. Значит, из слова ЫУЫУЫ нельзя разрешенными операциями получить слово УЫУЫУ, и следовательно, нельзя утверждать, что эти слова обязательно имеют одинаковый смысл.

100 фишек выставлены в ряд. Разрешено менять местами две фишки, стоящие через одну фишку. Можно ли с помощью таких операций переставить все фишки в обратном порядке?

Решение. Пронумеруем места, на которых стоят фишки.

В итоге же картинка должна стать такой:

Итак, если изначально фишка стояла на четном месте, то должна оказаться на нечетном месте, но это невозможно, так как разрешено менять местами две фишки, стоящие через одну фишку (если фишка лежала на четном месте, то ее можно переложить только на четное место). То есть четность места фишки является инвариантом.

Круг разделен на 6 секторов, в каждом из которых стоит фишка-рыбка. Разрешается за один ход сдвинуть любые две фишки в соседние с ними сектора. Можно ли с помощью 20 таких операций собрать все фишки в одном секторе?

Решение. Занумеруем сектора по часовой стрелке числами от 1 до 6. Для любого расположения фишек рассмотрим величину S – сумму номеров секторов, в которых лежат данные нам 6 фишек (при этом если в каком-то секторе лежит две фишки, то его номер учитывается дважды, если три фишки – трижды и т.д. Например, для ситуации, приведенной на рис. эта величина равна 1+2+3+3+5+6=20). Тогда, если мы перекладываем фишку на соседний сектор, S меняется или на 1 или на 5 (если мы перекладываем с 1 на 6 или наоборот). В любом случае четность S меняется. Следовательно, после 20 ходов четность S будет такая же, как в начале. В начале S =1+2+3+4+5+6=21. А если бы все фишки лежали в одном секторе с номером n , то S равнялось бы 6n – четное число. Значит, собрать все фишки в одном секторе за 20 ходов не получится.

На доске написаны десять чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными?

Проследим за суммой всех чисел. При операции из условия эта сумма увеличивается на 2. Значит, четность суммы всех чисел не меняется, она инвариант. В начале сумма всех чисел равна 1+2+…+9+10=45. То есть сумма была нечетной. А если все числа сделать равными какому-то числу n , то их сумма станет равно 10n – четное число. Следовательно, сделать все числа равными невозможно.

Замечание. Сумму чисел от 1 до 10 можно подсчитать аналогично Замечанию 1. А можно не считать, а заметить что она нечетная так как в ней участвует 5 нечетных слагаемых – 1,3,5,7,9.

На доске написаны шесть чисел: 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными? (задача, аналогичная предыдущей).

На квадратном поле 10*10 девять клеток 1*1 поросли бурьяном. После этого бурьян может распространиться на клетку, у которой не менее двух соседних клеток уже поросли бурьяном. Докажите, что тем не менее бурьян не сможет распространиться на все клетки.

Как изменяется периметр области, поросшей бурьяном?

Рассмотрим границу области, поросшей бурьяном (т.е. все отрезки длиной 1 между узлами, по одну сторону от которых бурьян, а по другую — нет). Вначале длина границы была не более 9*4=36, поскольку бурьян рос только в девяти клетках. Нетрудно заметить, что в процессе распространения бурьяна длина границы не может увеличиваться. Но если бы все поле 10*10 в некоторый момент оказалось поросшим бурьяном, то длина границы стала бы равной 10*4=40, что противоречит соображениям, приведенным выше .

Для построения инвариантов иногда бывают полезны вспомогательные раскраски, т.е. разбиения рассматриваемых объектов на несколько групп (каждая группа состоит из объектов одного цвета).

Задача 1. С таблицей, где имеется 15 чисел (  1), а остальные равны 1, можно производить следующую операцию  изменить знак двух (не больше, не меньше) чисел в таблице. Можно ли применяя эту операцию конечное число раз, получить таблицу, состоящую из чисел (+1)?

Решение . Ответ очевиден: нельзя. Инвариантом таблицы относительно рассматриваемой операции является произведение всех чисел в таблице. В начальный момент это произведение равно (  1), а нам нужно получить таблицу, инвариант которой равен (+1).

Задача 2. Дана шахматная доска. Разрешается перекрашивать в другой цвет сразу все клетки какой-либо горизонтали или вертикали. Может ли при этом получиться доска, у которой ровно одна черная клетка?

Решение . При перекрашивании горизонтали или вертикали, содержащей k черных и 8  k белых клеток, получится 8  k черных клеток, и k белых клеток. Поэтому число черных клеток изменится на (8  k)  k= 8  2 k, т.е. на четное число. Т.к. четность числа черных клеток сохраняется, из исходных 32 черных клеток мы не можем получить одну черную клетку.

Задача 3. В каждой клетке доски 5х5 клеток сидит жук. В некоторый момент все жуки переползают на соседние по горизонтали или по вертикали клетки. Обязательно ли при этом останется пустая клетка?(есть в презентации)

Решение. Т.к. общее число клеток нечетно, то черных и белых клеток не может быть поровну. Пусть для определенности черных клеток больше, тогда жуков, сидящих на белых клетках, меньше, чем на черных клетках. Поэтому, хотя бы одна из черных клеток останется пустой, т.к. на черные клетки переползают жуки, сидящие на белых клетках.

Задача 4. На шести елках сидят шесть чижей, на каждой елке  по чижу. Елки растут в ряд с интервалами 10м. Если какой-то чиж перелетает с одной елки на другую, то какой-то другой чиж обязательно перелетает на столько же метров, но в обратном направлении. Могут ли все чижи собраться на одной елке? А если чижей и ёлок  семь?

а) Пронумеруем деревья с 1 по 6 и пусть первоначально на каждой елке сидит по чижу и каждый чиж имеет тот же номер, что и ель. Т. к. чижи перелетают на елки в разных направлениях, то сумма номеров чижей не меняется – инвариант.

Первоначально сумма была (1+6):2*6 = 21. Если предположить, что все чижи собрались на одной елке, то сумма номеров будет 6* n (т. к. все чижи получили номер елки, на которую прилетели), зн 6* n =21, n =3,5 – не натуральное. Значит предположение неверно и такого не может быть.

б) (1+7):2*7=28, 28=7 n ? N =4, значит все чижи могут собраться на ели № 4

Задача 5 Дно прямоугольной коробки вымощено плитками 1х4 и 2х2. Плитки высыпали из коробки, и одна плитка 2х2 потерялась. Её заменили на плитку 1х4. Докажите, что теперь дно коробки вымостить не удастся.

Рассмотрим раскраску в четыре цвета, указанную на рисунке:

Источник