Тема 2. Способы преобразования чертежа.
По теме 2 должны быть решены три задачи способами преобразования чертежа.В табл. 3 даны варианты координат вершин пирамиды SABC в миллиметрах.
Задача №1: Определить истинную величину основания АВС пирамиды. Вариант способа решения указан в табл. 3 индивидуальных заданий, а именно:
а) вращением вокруг горизонтали, или
б) вращением вокруг фронтали, или
в) совмещением с горизонтальной плоскостью проекций П1, или
г) совмещением с фронтальной плоскостью проекций П2.
Задача №2: Определить способом вращения без указания оси вращения расстояние от вершины S до плоскости основания (высоту пирамиды) и угол наклона плоскости основания к горизонтальной (или фронтальной, в зависимости от варианта) плоскости проекций.
Задача №3: Определить способом замены плоскостей проекций:
а) величину двугранного угла между гранями, указанными в задании (см. табл. 3), или
б) кратчайшее расстояние между ребрами пирамиды и стороной ее основания с построением проекций искомого отрезка в основной системе плоскостей проекций.
В первой задаче для определения истинной величины основания АВС пирамиды нужно, применив способ вращения, поставить плоскость треугольника АВС в положение параллельное одной из плоскостей проекций или совместит с одной из них. Тогда на эту плоскость проекций треугольник АВС спроецируется в истинную величину.
Если треугольник повернуть вокруг одной из его горизонталей, то он займет положение параллельное горизонтальной плоскости проекций. Если за ось вращения выбрать фронталь, то треугольник АВС можно повернуть до положения параллельного фронтальной плоскости проекций. При вращении плоскости основания АВС вокруг горизонтального следа совмещают ее с плоскостью проекций П1, а вращением вокруг фронтального – с плоскостью проекций П2.
На рис. 3 истинная величина треугольника АВС определена вращением его вокруг горизонтали А 1 до положения параллельного плоскости проекций П1.
Решение задачи ведется по следующему плану:
1) проводится ось вращения (А1);
2) строятся плоскости вращения для каждой вращаемой вершины (θ и Σ, перпендикулярные к А1);
3) находятся центры вращения (О и О 1 ) каждой вращаемой вершины;
4) определяется истинная величина радиуса вращения (О1 В0) вершины В;
5) находятся положения точек (В¹1 и С1)после осуществления процесса вращения на следах их плоскостей вращения.
Во второй задаче искомое расстояние от вершины S до основания АВС пирамиды измеряется величиной перпендикуляра, опущенного из точки S на плоскость основания. Если способом вращения вокруг оси, перпендикулярной к одной из плоскостей проекций, поставить треугольник АВС в положение, перпендикулярное к другой плоскости проекций (т. е. в проецирующее), то перпендикуляр к плоскости ∆АВС, опущенный из точки S, окажется параллельным этой плоскости проекций и спроецируется на нее в истинную величину.
Основание пирамиды АВС, заняв проецирующее положение, изобразиться на плоскости проекций к которой оно перпендикулярно, и в виде отрезка прямой линии и угол наклона этого отрезка к оси Х составит линейный угол, которым будет измеряться двугранный угол наклона плоскости основания пирамиды к той плоскости проекций, перпендикулярно к которой была выбрана ось вращения. Поэтому, если требуется определить угол наклона плоскости основания к плоскости проекций П1, то за ось вращения следует выбирать прямую, перпендикулярную к П1, а если нужно узнать угол наклона к плоскости проекций П2, то и ось вращения должна быть перпендикулярна к этой плоскости проекций. Однако, если учесть, что размеры и форма горизонтальной проекции плоской фигуры не измеряется, если ось вращения перпендикулярна к горизонтальной плоскости проекций, то и ось вращения на эпюре можно не указывать, а лишь подразумевать.
На рис.3 наряду с определением расстояния от точки S до плоскости основания пирамиды определен угол наклона основания к плоскости проекций П1(угол α).
Задача решалась по следующему плану:
1. Ось вращения подразумевали расположенной перпендикулярно к плоскости проекций П1;
2. Горизонтальную проекцию пирамиды А1В1С1S1 перевели в новое положение, не измеряя ее формы и размеров так, чтобы горизонтальная проекция А111 горизонтали треугольника АВС заняла положение перпендикулярное к оси Х (это соответствует тому, что в пространстве горизонталь А1, а вместе с ней и плоскость основания АВС оказались перпендикулярны к плоскости проекций П2);
3. На фронтальной плоскости проекций провели следы плоскостей вращения параллельно оси Х для всех вращаемых вершин;
4. Построили фронтальные проекции вершин плоскости основания АВС (отрезок прямой) и вершины S;
5. Построили истинную величину высоты пирамиды, опустив перпендикуляр из нового положения проекции S2 2 точки S на проекцию ∆АВС (отрезок С2 2 В2 2 ) и нашли горизонтальную проекцию перпендикуляра;
6. Отметили угол наклона фронтальной проекции ∆АВС (отрезок прямой С2 2 В 2 2) к оси Х (угол α), которым измеряется угол наклона плоскости основания пирамиды к плоскости проекций П1.
Третья задача решается способом замены плоскостей проекций. Если при решении задачи в задании требуется определить величину двугранного угла между гранями пирамиды, то нужно так преобразовать чертеж, чтобы общее для этих граней ребро заняло положение перпендикулярное к одной из плоскостей проекций, так как мерой двугранного угла между гранями служит линейный угол, который получается в результате пересечения граней плоскостью, перпендикулярной к общему ребру.
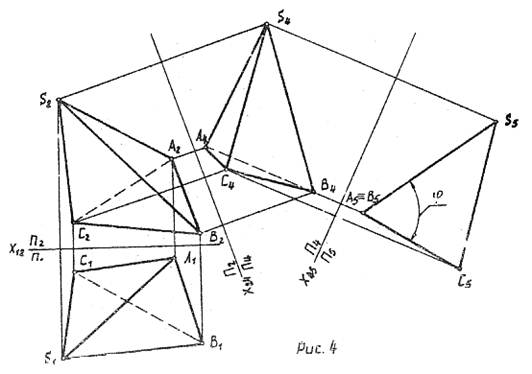
На рис.4 показано определение угла между гранями АВС и АВS (угла φ) для этого ребро АВ поставлено в положение перпендикулярное к плоскости проекцийП5.
План решения задачи:
1. Заменяем плоскость проекций П1 на П4 и ставим последнюю в положение параллельное ребру АВ (ось Х24 параллельна А2В2);
2. Заменяем плоскость проекций П2 на П5, располагая плоскость П5 перпендикулярно к ребру АВ (ось Х43 ┴ А1В4).
На плоскость проекций П5 ребро АВ выродится в точку и искомый линейный угол спроецируется без искажения.
Для определения кратчайшего расстояния между двумя скрещивающимся ребрами следует так сменить плоскости проекций, чтобы одно из этих ребер спроецировалось на плоскость проекций в виде точки(заняло проецирующее положение). Тогда истинная величина искомого расстояния будет равна проекции отрезка перпендикуляра, спущенного из этой точки на проекции второй прямой.
Источник
Тема 1. Способы преобразование чертежа
По теме 1 должны быть решены три задачи способами преобразования чертежа.
В табл. 3. Даны варианты координат вершин пирамиды SABC в миллиметрах.
Задача № 1. Определить истинную величину основания ABC пирамиды. Вариант способа решения указан в табл. 4 индивидуальных заданий, а именно :
а) вращением вокруг горизонтали, или
б) вращением вокруг фронтали, или
в) совмещение с горизонтальной плоскостью проекций П1, или
г) совмещение с фронтальной плоскостью проекций П2.
Задача № 2. Определить способом вращения без указания оси вращения расстояние от вершины S до плоскости основания (высоту пирамиды) и угол наклона плоскости основания к горизонтальной (или фронтальной, в зависимости от варианта ) плоскости проекций.
Задача № 3. Определить способом замены плоскостей проекций:
а) величину двугранного угла между гранями, указанными в задании (см. табл. 3), или
б) кратчайшее расстояние между ребрами пирамиды и стороной ее основания с построением проекций искомого отрезка в основной системе плоскостей проекций.
Таблица 3
| варианты | точки | Координаты (мм) | варианты | точки | Координаты (мм) |
| х | у | z | х | у | z |
| С 1 по 4 | А | С 41 по 44 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 5 по 8 | А | С 45 по 48 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 9 по 12 | А | С 49 по 52 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 13 по 16 | А | С 53 по 56 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 17 по 20 | А | С 57 по 60 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 21 по 24 | А | С 61 по 64 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 25 по 28 | А | С 65 по 68 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 29 по 32 | А | С 69 по 72 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 33 по 36 | А | С 73 по 76 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 37 по 40 | А | С 77 по 80 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| варианты | точки | Координаты (мм) | варианты | точки | Координаты (мм) |
| х | у | z | х | у | z |
| С 81 по 84 | А | С 93 по 96 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 85 по 88 | А | С 97 по 100 | А | ||
| В | В | ||||
| С | С | ||||
| S | S | ||||
| С 89 по 92 | А | ||||
| В | |||||
| С | |||||
| S |
Таблица 4
| № варианта | Тема 1 | |
| Задача № 1 | Задача № 2 | Задача № 3 |
| Применить способ вращения или совмещения | Найти угол наклона к плоскости проекций | Найти угол между гранями или расстояние между ребрами |
| Вокруг горизонтали | П1 | Грани SAB и ABC |
| Вокруг фронтали | П2 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SAC и АСВ |
| Совместить с пл. пр. П2 | П1 | Ребра SB и АС |
| Вокруг фронтали | П2 | Ребра SC и АВ |
| Вокруг горизонтали | П1 | Грани SBC и АСВ |
| Совместить с пл. пр. П2 | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SAB и АВС |
| Вокруг горизонтали | П1 | Ребра SB и АС |
| Вокруг фронтали | П2 | Грани SAC и АВС |
| Совместить с пл. пр. П1 | П1 | Ребра SC и АВ |
| Совместить с пл. пр. П2 | П2 | Грани SBC и АСВ |
| Вокруг горизонтали | П2 | Грани SAB и ABC |
| Вокруг фронтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SAC и АСВ |
| Совместить с пл. пр. П2 | П1 | Ребра SB и АС |
| Совместить с пл. пр. П1 | П2 | Грани SBC и АСВ |
| Совместить с пл. пр. П2 | П2 | Грани SAC и АСВ |
| Вокруг горизонтали | П1 | Ребра SC и АВ |
| Вокруг фронтали | П1 | Ребра SB и АС |
| Вокруг горизонтали | П2 | Грани SAB и ABC |
| Вокруг фронтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SBC и АСВ |
| Совместить с пл. пр. П2 | П1 | Ребра SB и АС |
| Вокруг фронтали | П2 | Грани SAB и ABC |
| Совместить с пл. пр. П2 | П1 | Ребра SC и АВ |
| Вокруг горизонтали | П1 | Грани SAC и SAB |
| Совместить с пл. пр. П1 | П2 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П1 | Грани SBC и SBA |
| Вокруг горизонтали | П2 | Ребра SB и АС |
| Вокруг фронтали | П2 | Грани SAB и SAC |
| Совместить с пл. пр. П2 | П1 | Ребра SC и АВ |
| Вокруг горизонтали | П2 | Грани SAC и SAB |
| Вокруг фронтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SBC и SBA |
| Совместить с пл. пр. П2 | П1 | Ребра SB и АС |
| Вокруг фронтали | П2 | Грани SAB и SAC |
| Вокруг горизонтали | П1 | Ребра SC и АВ |
| Совместить с пл пр. П1 | П2 | Грани SAB и АВС |
| Совместить с пл. пр. П2 | П1 | Ребра SA и ВС |
| Вокруг горизонтали | П2 | Грани SBC и АВС |
| Совместить с пл. пр. П1 | П1 | Ребра SB и АС |
| Вокруг фронтали | П2 | Грани SAC и АВС |
| Совместить с пл. пр. П2 | П1 | Ребра SC и АВ |
| Вокруг горизонтали | П2 | Грани SAB и АВС |
| Вокруг фронтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SBC и АВС |
| Совместить с пл. пр. П2 | П1 | Ребра SB и АС |
| Вокруг фронтали | П2 | Грани SAC и АВС |
| Вокруг горизонтали | П1 | Ребра SC и АВ |
| Совместить с пл. пр. П2 | П2 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П1 | Грани SAB и АВС |
| Вокруг горизонтали | П2 | Грани SAC и АВС |
| Вокруг фронтали | П1 | Ребра SB и AC |
| Совместить с пл. пр. П1 | П2 | Ребра SC и АВ |
| Совместить с пл. пр. П2 | П1 | Грани SBC и АВС |
| Вокруг фронтали | П2 | Грани SAB и АВС |
| Вокруг горизонтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П2 | П2 | Грани SBC и АВС |
| Совместить с пл. пр. П1 | П1 | Ребра SB и АС |
| Вокруг горизонтали | П2 | Грани SAC и АВС |
| Совместить с пл. пр. П1 | П1 | Ребра SC и АВ |
| Вокруг фронтали | П2 | Грани SAB и АВС |
| Совместить с пл. пр. П2 | П1 | Ребра SA и ВС |
| Вокруг фронтали | П2 | Грани SBC и АВС |
| Вокруг горизонтали | П1 | Ребра SB и АС |
| Совместить с пл. пр. П1 | П2 | Грани SAC и SBC |
| Совместить с пл. пр. П2 | П1 | Ребра SC и АВ |
| Вокруг горизонтали | П2 | Грани SAB и SBC |
| Вокруг фронтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SAC и АВС |
| Совместить с пл. пр. П2 | П1 | Ребра SB и АС |
| Вокруг горизонтали | П2 | Грани SBC и АВС |
| Вокруг фронтали | П1 | Ребра SC и АВ |
| Совместить с пл. пр. П2 | П2 | Грани SAB и АSC |
| Совместить с пл. пр. П1 | П1 | Ребра SA и ВС |
| Вокруг горизонтали | П2 | SAC SBC |
| Совместить с пл. пр. П2 | П1 | SB |
| Вокруг фронтали | П2 | SBC ABS |
| Совместить с пл. пр. П1 | П2 | Ребра SC и АВ |
| Вокруг фронтали | П1 | Ребра SA и ВС |
| Совместить с пл. пр. П1 | П2 | Грани SBC и ABC |
| Вокруг горизонтали | П1 | Грани SAB и ABC |
| Совместить с пл. пр. П2 | П2 | Ребра SB и AC |
| Вокруг горизонтали | П1 | Грани SAC и ABC |
| Вокруг фронтали | П2 | Ребра SC и АВ |
| Совместить с пл. пр. П1 | П1 | Грани SBC и ABS |
| Совместить с пл. пр. П2 | П2 | Ребра SA и ВС |
| Вокруг фронтали | П1 | Грани SAB и ASC |
| Вокруг горизонтали | П2 | Ребра SB и AC |
| Совместить с пл. пр. П1 | П1 | Грани SAC и SBC |
| Совместить с пл. пр. П2 | П2 | Ребра SC и АВ |
| Вокруг горизонтали | П1 | Грани SBC и ABC |
| Совместить с пл. пр. П1 | П2 | Ребра SA и ВС |
| Вокруг фронтали | П1 | Грани SAB и ABC |
| Совместить с пл. пр П2 | П2 | Ребра SB и AC |
| Вокруг фронтали | П1 | Грани SAC и SBC |
| Вокруг горизонтали | П2 | Ребра SC и АВ |
| Совместить с пл. пр. П1 | П1 | Грани SBC и ABS |
| Совместить с пл. пр. П2 | П2 | Ребра SA и ВС |
В первой задаче для определения истиной величины основания АВС пирамиды нужно, применив способ вращения, поставить плоскость треугольника АВС в положение параллельное одной из плоскостей проекций или совместить с одной из них. Тогда на эту плоскость проекций треугольник АВС спроецируется в истинную величину.
Если треугольник повернуть вокруг одной из его горизонталей, то он займет положение параллельное горизонтальной плоскости проекций. Если за ось вращения выбрать фронталь, то треугольник АВС можно повернуть до положения параллельного фронталньой плоскости проекций. При вращении плоскости основания АВС вокруг горизонтального следа совмещают ее с плоскостью проекций П1, а вращение вокруг фронтального — с плоскостью проекций П2.
На рис. 3 истинная величина треугольника АВС определена вращением его вокруг горизонтали А1 до положения параллельного плоскости проекций П1.
Решение задачи ведется по следующему плану:
1) проводится ось вращения (А1);
2) строятся плоскости вращения для каждой вращаемой вершины (Θ и Σ перпендикулярные к А1);
3) находятся центры вращения (О и О 1 ) каждой вращаемой вершины;
4) определяется истинная величина радиуса вращения (О1В0) вершины В;
5) находятся положения точек (В1 1 и С1 1 ) после осуществления процесса вращения на следах их плоскостей вращения.
Во второй задаче искомое расстояние от вершины S до основания АВС пирамиды измеряется величиной перпендикуляра опущенного из точки S на плоскость основания. Если способом вращения вокруг оси, перпендикулярной к одной из плоскостей проекций, поставить треугольник АВС в положение, перпендикулярное к другой плоскости проекций (т.е. в проецирующее), то перпендикуляр к плоскости ∆ АВС, опущенный из точки S, окажется параллельным этой плоскости проекций и с проецируется на нее в истинную величину.
Основание пирамиды АВС, заняв проецирующее положение, изобразится на плоскости проекций, к которому оно перпендикулярно, в виде отрезка прямой линии и угол наклона этого отрезка к оси Х составит линейный угол, которым будут измеряться другранный угол наклона плоскости основания пирамиды к той плоскости проекций, перпендикулярно к которой была выбрана ось вращения. Поэтому, если требуется определить угол наклона плоскости основания к плоскости проекций П1, то за ось вращения следует выбирать прямую, перпендикулярную к П1, а если нужно узнать угол наклона к плоскости проекций П2, то и ось вращения должна быть перпендикулярна к этой плоскости проекций. Однако, если учесть, что размеры и форма горизонтальной проекции плоской фигуры не изменяется, если ось вращения перпендикулярна к горизонтальной плоскости проекций, то и ось вращения на эпюре можно не указывать, а лишь подразумевать.
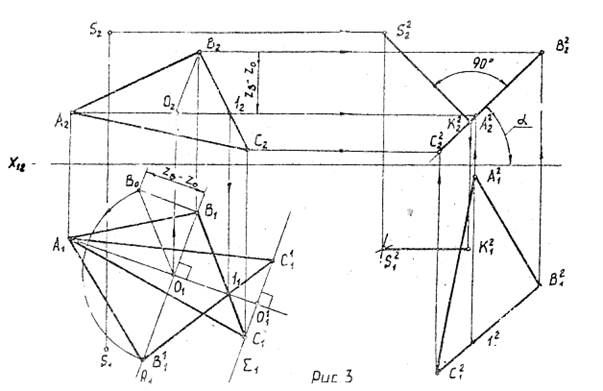 |
На рис. 3 наряду с определение расстояния от точки S до плоскости основания пирамиды определен угол наклона основания к плоскости проекций П1 (угол α).
Задача решалась по следующему плану:
1) ось вращения подразумевали расположенной перпендикулярно к плоскости проекций П1)
2) горизонтальную проекцию пирамиды А1В1С1S1 перевели в новое положение, не изменяя ее формы и размеров так, чтобы горизонтальная проекция А111 горизонтали треугольника АВС заняла положение перпендикулярное к оси Х (это соответствует тому, что в пространстве горизонталь А1, а вместе с ней и плоскость основания АВС оказались перпендикулярны к плоскости проекций П2);
3) на фронтальной плоскости проекций провели следу плоскостей вращения параллельно оси Х для всех вращаемых вершин;
4) построили фронтальные проекции вершин плоскости основания АВС (отрезок прямой) и вершины S;
5) построили истинную величину высоты пирамиды, опустив перпендикуляр из нового положения проекции S2 2 точки S на проекцию ∆ АВС (отрезок С2 2 В2 2 ) и нашли горизонтальную проекцию перпендикуляра;
6) отметили угол наклона фронтальной проекции ∆ АВС (отрезок прямой С2 2 В2 2 ) к оси Х (угол α), которым измеряется угол наклона плоскости основания пирамиды к плоскости проекций П1.
Третья задача решается способом замены плоскостей проекций. Если при решении задачи в задании требуется определить величину двугранного угла между гранями пирамиды, то нужно так преобразовать чертеж, чтобы общее для этих граней ребро заняло положение перпендикулярное к одной из плоскостей проекций, так как мерой двугранного угла между гранями служит линейный угол, который получается в результате пересечения граней плоскостью, перпендикулярной к общему ребру.
На рис. 4 показано определение угла между гранями АВС и АВС (угла φ) для этого ребро АВ поставлено в положение перпендикулярное к плоскости проекций П5.
План решения задачи:
1)
 |
заменяем плоскость проекций П1 на П4 и ставим последнюю в положение параллельное ребру АВ (ось х2 4 параллельна А2В2);
2) заменяем плоскость проекций П2 на П5, располагая плоскость П5 перпендикулярно к ребру АВ (ось х45 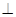
На плоскость проекций П5 ребро АВ выродится в точку и искомый линейный угол спроецируется без искажения.
Для определения кратчайшего расстояния между двумя скрещивающимися ребрами следует так сменить плоскости проекций, чтобы одно из этих ребер спроецировалось на плоскость проекций в виде точки (заняло проецирующее положение). Тогда истинная величина искомого расстояния будет равна проекции отрезка перпендикуляра, опущенного из этой точки на проекцию второй прямой.
Источник





