Дана пирамида abcs применяя способы преобразования чертежа определить высоту пирамиды

Дана пирамида abcs применяя способы преобразования чертежа определить высоту пирамиды

1) Соединяешь все точки в линии, те которые не видимы пунктиром.
2) Проводишь горизонталь, сверху и снизу
3) Проводишь фронталь, сверху и снизу
4) Из точки S2 перпендикулярно фронтали проводишь прямую L2
5) Из точки S1 перпендикулярно горизонтали проводишь прямую L1
6) Точка пересечения линии A2C2 — 3(2) проецируешь и получаешь 3(1)
7) Точка пересечения линии В2C2 — 4(2) проецируешь и получаешь 4(1)
8) Пересечение линии 3(1)-4(1) с прямой L1 получаешь точку D1
9) Проецируешь D2
10) Строишь разность высот с точками A2-D2 и S2-D2
11) От линии A1-D1 проводишь перпендикуляр из точки A1 на расстояние разницы высот A2-D2. Соединяешь их в треугольник, гипотенуза = H.B.[AD]
12) От линии S1-D1 проводишь перпендикуляр из точки S1 на расстояние разницы высот S2-D2. Соединяешь их в треугольник, гипотенуза = H.B.[SD]
13) В левом нижнем углу берём точку, обзываем её D, из неё строим под прямым углом (то есть перпендикулярно друг к другу) две линии:
вверх, линию, равную по размерам H.B.[SD], самую верхнюю точку данной линии обзываем S,
вниз, линию, равную по размерам H.B.[AD], самую правую точку данной линии обываем A,
Соединяем эти две точки (S и A), получаем треугольник.
Если данный треугольник в самом левом нижнем углу не помещается в связи со своими размерами, то разрешается его запихнуть, куда-нибудь в другое место, но желательно внизу чертежа.

Строим изометрию:
Рисуем одну вертикальную линию — Z ось.
От нижней точки оси Z под с помощью угольника откладываем 60 градусов в правую сторону и получаем ось Y, переворачиваем угольник и строим ось влево, получаем ось X. Таким образом, каждая ось находится друг от друга под 120 градусов.
Теперь но оси X откладываем точки A, B, C, S и D (то есть по иксу). Берём инженерную линейку, она же Рейсшина, проводим относительно оси Y параллель из точек A, B, C, S и D, на соответствующее им расстояние по Y. Расстояние для откладывания берём из чертежа и задания на РГР. Полученные точки обзываем A1′ B1′ C1′ S1′ и D1′.
Берём ещё раз рейсшину и параллельно вертикальной оси Z откладываем на соответственное расстояние точки вверх от точек A1′ B1′ C1′ S1′ и D1′. Обзываем полученные точки A’ B’ C’ S’ и D’.
Соединяем точки в линиях:
A1′-B1′ A1′-C1′ B1′- C1′ A1′-S1′ B1′-S1′ C1′-S1′
D1′-S1′
A’-B’ A’-C’ B’- C’ A’-S’ B’-S’ C’-S’
D’-S’
Диметрия строится так же, только угол у нею будет не 120 градусов всех линий друг к другу.

Надписи:
Все надписи делать 7 шрифтом. Разрешается от руки, приближенного к ГОСТ.
В правом, верхнем углу записываем координаты точек A, B, C, S по осям X, Y, Z. Если не помещается прямоугольником вниз, можно развернуть прямоугольником вправо.
Затем, над чертежом Изометрии/Диметрии записываете задание НАКЛОННЫМ шрифтом:
«Построить проекции и определить натуральную величину высоты SD пирамиды и угла наклона ребра AS к основанию ABC. Построить аксонометрическую проекцию пирамиды и ее высоты». Переносы допускаются.

Источник

Дана пирамида abcs применяя способы преобразования чертежа определить высоту пирамиды

Пошаговый алгоритм решения задачи №2 — Построение проекций наклонной пирамиды

Необходимо построить наклонную пирамиды по известному основанию и высоте.

Для решения задачи необходимо знать теоретический материал:

— способы восстановления перпендикуляра к плоскости;

— определение натуральных величин методом вращения;

— определение видимости на чертеже с помощью конкурирующих точек (рассматривали в задаче 1).

Порядок решения задачи

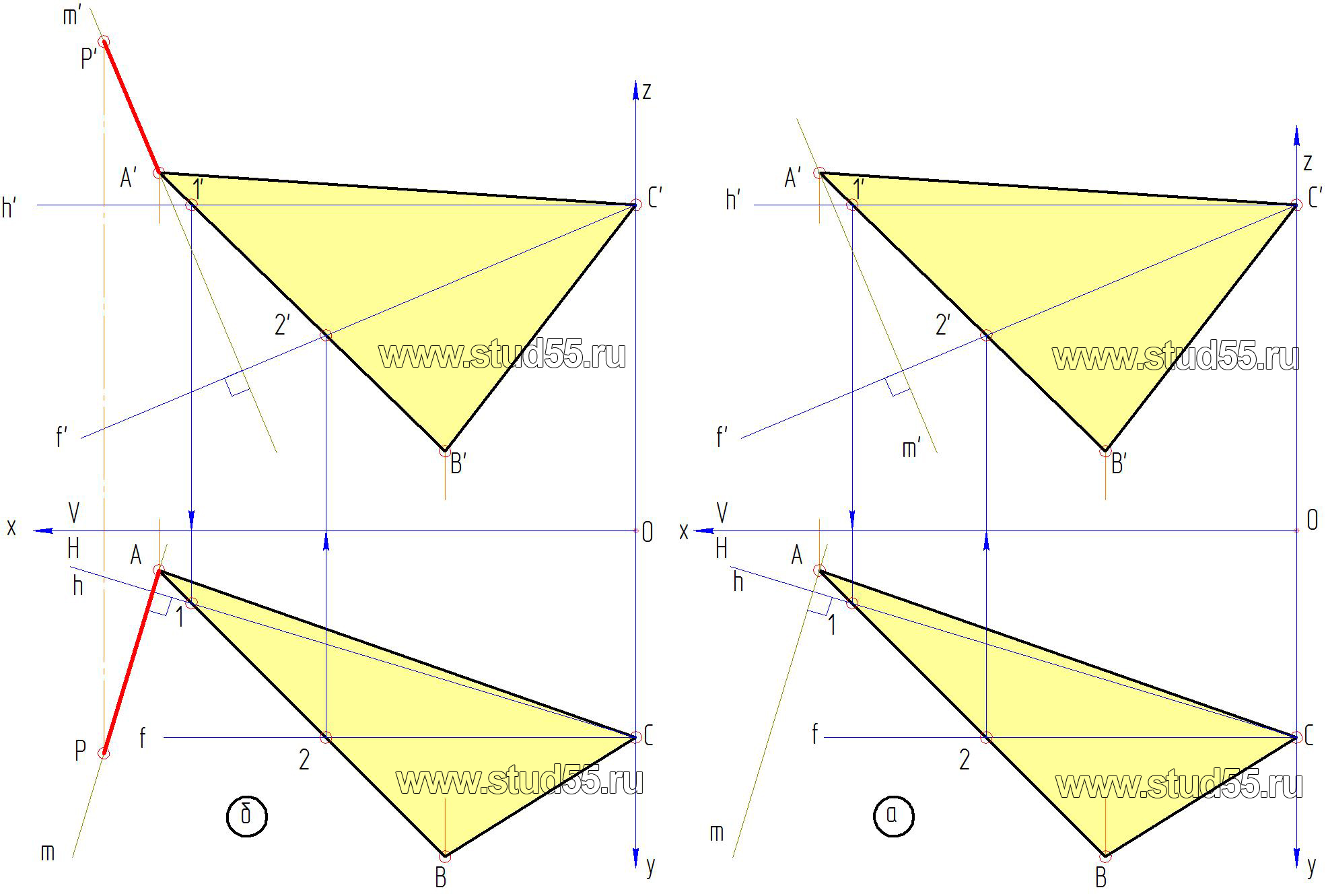
1. Согласно варианту задания наносим на комплексный чертеж координаты точек основания пирамиды, получаем плоскость в виде треугольника ABC(A’B’C’; ABC) (рис.2.1.a).

Рис. 2.1

2. Для нахождения вершины пирамиды по заданной высоте необходимо к указанной плоскости провести перпендикуляр через точку А (A’; A) т.к. величина высоты задана SA, для чего:

— в заданной плоскости треугольника основания пирамиды проводим горизонталь h’и h и фронталь – f’ и f (рис.2.1.б).

— к проекциям горизонтали и фронтали, которые выражены в натуральной величине через точку А(A’; A) проводим перпендикуляр m (рис.2.2.а).

Рис.2.2

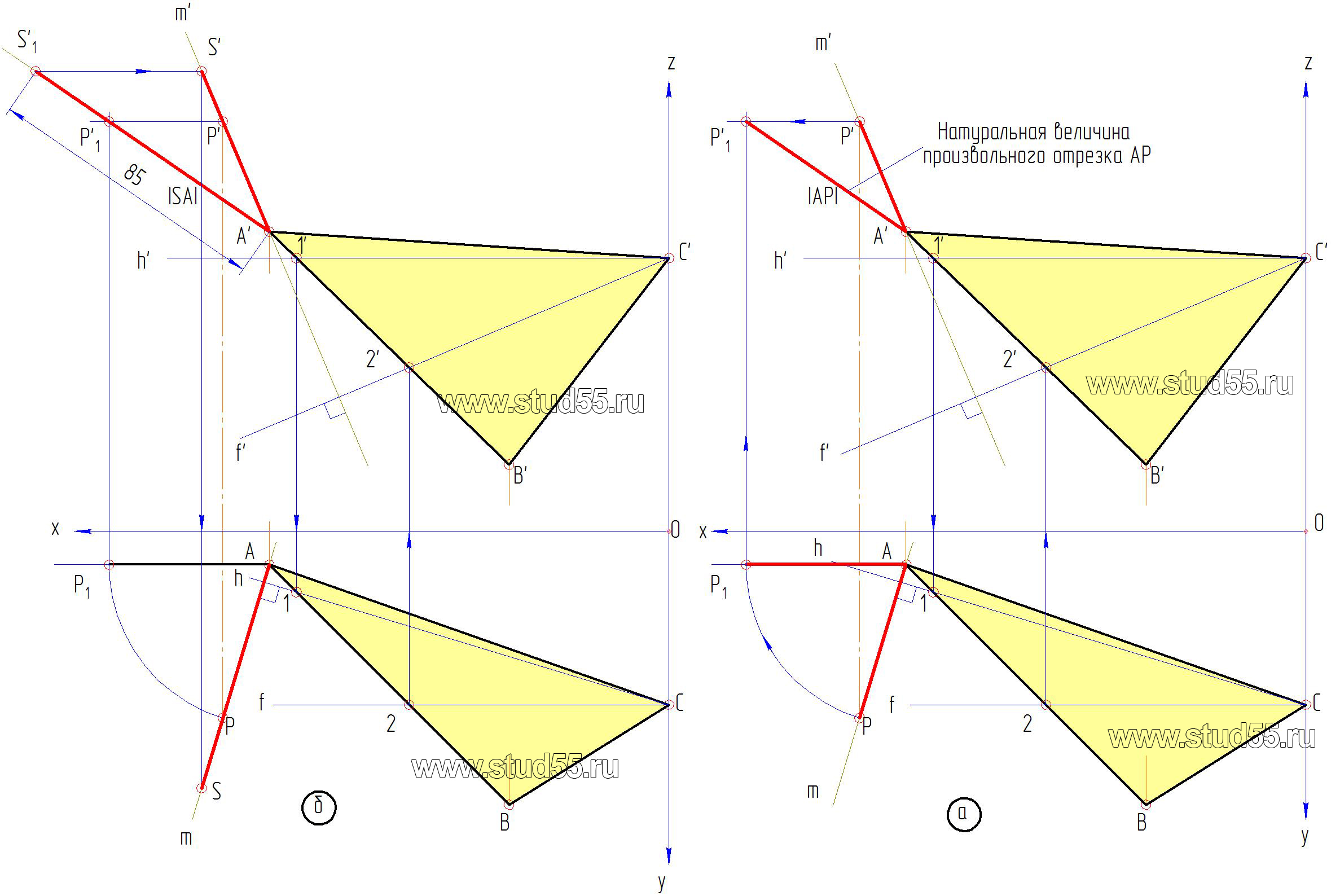
3. Так как высота пирамиды задана в натуральной величине, а проведенный перпендикуляр — в проекциях, необходимо получить линию натуральной величины произвольного отрезка на перпендикуляре. Для этого воспользуемся методом вращения:

-на проекциях перпендикуляра возьмем произвольную точку P (P’ и Р) (рис.2.2.б);

— отрезок AР в горизонтальной проекции переведем в частное положение путем разворота его вокруг точки A, до параллельности оси х, получим точку P₁ (рис.2.3.а).

— можно отметить, что при вращении точки в какой-то плоскости ее проекция на сопряженной плоскости движется по прямой параллельной оси х. Проведем ее из точки P’ и тогда по линиям связи на ней находим фронтальную проекцию точки P —P’₁

— соединив P’₁ и A’ получим линию натуральной величины отрезка перпендикуляра, на котором откладываем заданное расстояние SA (h=85мм), получая S’₁ — истинное положение вершины пирамиды.

4. Переведем истинную вершину пирамиды S’₁ на фронтальную проекцию перпендикуляра по линии параллельной оси х получаем S’ — фронтальную проекцию вершины пирамиды. По линии связи получаем ее горизонтальную проекцию – S (рис.2.3.б).

Рис.2.3

5. Таким образом, вершина пирамиды S (S’ и S) построена, соединяем ее с основанием и в заключение определяем видимость ребер пирамиды, для чего:

— возьмем на горизонтальной проекции две конкурирующие точки 3 и 4, принадлежащие соответственно линиям SC и AB спроецируем данные точки на фронтальную плоскость, получим 3’ и 4’ на линиях S’C’ и A’B’;

— по правилу определения видимости с помощью конкурирующих точек определяем, что прямая SC, в горизонтальной проекции будет видимой, т.к. ордината точки 3’, находящаяся на ней во фронтальной плоскости больше, чем ордината точки 4’, а линия AB будет невидимой (рис.2.4.а);

— аналогично определяем видимость во фронтальной плоскости, беря пару конкурирующих точек 5’ и 6’, находящихся на прямых S’B’ и A’C’. По выше изложенному правилу S’B’ на фронтальной плоскости проекций будет видимой, а A’C’–невидимой (рис.2.4.б).

Источник

Задача №1. Определить натуральную величину основания АВС пирамиды SABC

Задачу решаем способом вращения вокруг оси, параллельной плоскости проекций (горизонтали) Повернем плоскость DАВС вокруг горизонтали h этого треугольника в положение, параллельное плоскости П₁.

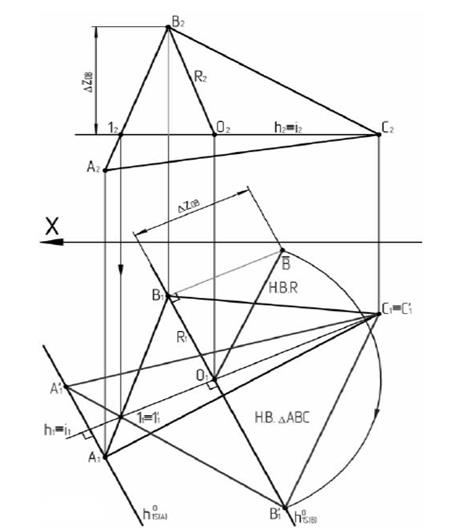
Необходимые геометрические построения для поворота DАВС выполняются в следующей последовательности (рис. 34):

1.Проводим фронтальную проекцию горизонтали DАВС, h₂ || оси Х, которая определяется точками С₂ и 1₂.

2. Пользуясь точками С₂, 1₂, находим точки С₁ и 1₁, определяющие горизонтальную проекцию горизонтали h₁, которая является осью вращения.

3.Поворачиваем точки треугольника вокруг принятой оси вращения. Точки С и 1, как принадлежащие оси вращения, не изменяют своего положения в процессе преобразования. Поэтому достаточно повернуть точки А и В.

Вращение точки В.

3.1.1. Через точку В₁ проводим горизонтальный след плоскости вращения h 0 _1S(В) перпендикулярно горизонтальной проекции горизонтали h₁ (с этой прямой будет совпадать горизонтальная проекция окружности, по которой перемещается точка В при ее вращении вокруг горизонтали).

3.1.2. Находим проекции центра вращения: О₁ – это точка пересечения плоскости вращения с осью вращения (h 0 _1S(В) Ç h₁), по линии связи определяется ее фронтальная проекция (О₂ Î h₂).

3.1.3. Определяем натуральную величину радиуса вращения, проекции которого О₁В₁ и О₂В₂, методом прямоугольного треугольника (можно любым другим способом).

3.1.4. Из центра О₁ проводим дугу радиусом О₁ до пересечения с плоскостью вращения – это и есть новое положение горизонтальной проекции точки В, В¢₁.

3.2. Точка А вращается в горизонтально-проецирующей плоскости, след которой проведен из точки А₁ перпендикулярно оси вращения, т.е. h₁ (h 0 _1S(А) ^ h₁). Следовательно, новое положение горизонтальной проекции точки А будет находиться на этом следе. Зная, что точка А лежит на продолжении отрезка В1, горизонтальную проекцию отрезка В¢₁1₁ продолжаем до пересечения с h 0 _1S(А), получаем новое положение горизонтальной проекции точки А, А¢₁. Для определения А¢₁ можно произвести построения, описанные для точки В.

4. После такого поворота плоскость треугольника АВС переведена в положение, параллельное плоскости П₁, а значит, ее новая горизонтальная проекция А¢₁ В¢₁ С¢₁ и есть натуральная величина.

Задача №2. Прямая АВ — общего положения (рис. 35). Повернуть АВ вокруг оси i, перпендикулярной к П₁, на угол j.

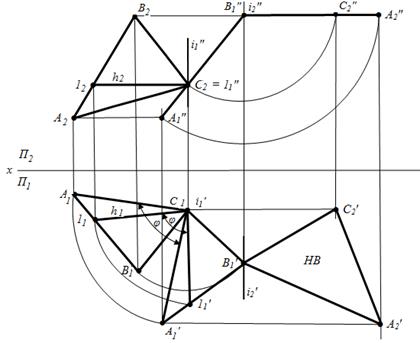
Новое положение горизонтальных проекций точек А и В находим путем вращения вокруг i′ на угол j. Для получения А₂¢ и В₂¢ проведем перпендикуляры из А₁′ и В₁′ к оси x соответственно и отметим точку их пересечения с горизонтальными прямыми, проведенными из А₂ и В₂ (поскольку точки А и В вращали вокруг оси i, перпендикулярной к П₁, то их координата z не изменилась).

Задача №3. Плоскость АВС — общего положения (рис. 36). Определить натуральную величину треугольника АВС.

Задача решается в два этапа. Сначала плоскость переводят в проецирующее положение. Для этого в плоскости АВС проводят горизонталь h и переводят ее в фронтально-проецирующее положение путем вращения вокруг оси i₁, перпендикулярной к П₁. Затем вращают остальные точки плоскости (А, В, С) на угол j. Таким образом, получим фронтально-проецируюшую плоскость А₁В₁С. Второй этап заключается в переводе А₁¢В₁¢С₁ в плоскость уровня. Ее вращают вокруг оси i₂, перпендикулярной к П₂. Получим горизонтальную плоскость уровня А¢₂В¢₁С¢₂, которая определяет натуральную величину заданной плоскости.

Выполнил студент

________________________________

Группа

__________________

Вопросы для подготовки

1. Как может располагаться ось вращения относительно плоскостей проекций?

2. Как перемещаются проекции точки при вращении вокруг оси, перпендикулярной к плоско

3. Какие основные операции на чертеже необходимо выполнить при вращении точки вокруг оси перпендикулярной к плоскости проекций П₁ или П₂?

4. В чем сущность способа плоскопараллельного перемещения? В чем его отличие от способа вращения вокруг проецирующей оси?

5. В чем сущность способа вращения вокруг лини уровня?

6. В чем состоит способ преобразования чертежа методом совмещения?

Задачи

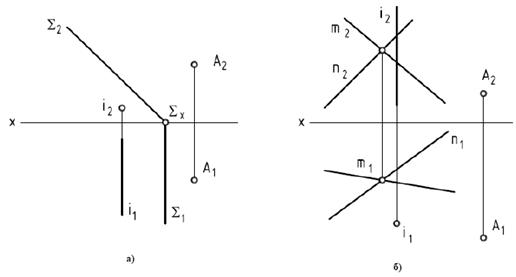
6.1. Вращением вокруг оси i совместить точку А с плоскостью
а) проецирующей S(S₁, S₂); б) общего положения S(m, n).

6.2. Вращением вокруг проецирующей оси преобразовать:

а) отрезок АВ общего положения в положение проецирующее;

б) треугольник АВС общего положения в положение плоскости уровня.

Выполнил студент

________________________________

Группа

__________________

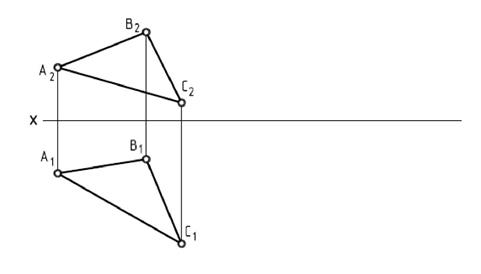
6.3. Определить натуральную величину треугольника АВС способом плоскопараллельного перемещения.

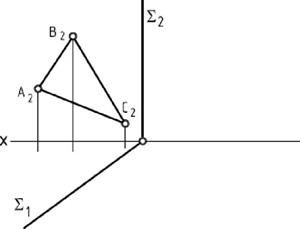
6.4. Определить натуральную величину треугольника АВС, расположенного в плоскости S(S1, S2).	6.5. Построить проекции биссектрисы угла А, применив вращение вокруг горизонтали.

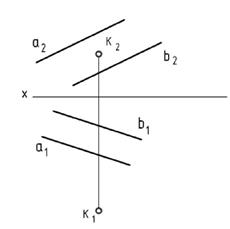
6.6.Определить расстояние от точки К до плоскостями S(a, b) а || b.

Последнее изменение этой страницы: 2017-03-15; Просмотров: 3202; Нарушение авторского права страницы

Источник