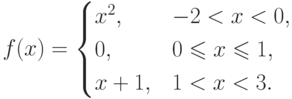Чтобы задать нужно указать способ закон правило с помощью которого для каждого значения

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Совокупности и отношения

Чтобы задать функцию, нужно указать некоторый способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции, то есть способ описания закона f . Функция может задаваться аналитическим, графическим, табличным или словесным способом.

Аналитическое выражение — формула, указывающая, какие математические действия надо произвести над аргументом x , чтобы получить соответствующие значения y . Способ задания значений функции с помощью аналитического выражения называется аналитическим способом задания функции . Функция может быть задана и с помощью нескольких различных аналитических выражений с разными областями определения. В этом случае область определения функции — область определения каждого из этих аналитических выражений (при условии, что эти отдельные области нигде «не конфликтуют»). Аналитически функция задается, если область ее определения не является конечной, особенно, в теоретических проблемах.

Пример.Рассмотрим кусочно-аналитически заданную функцию

При табличном задании функции ряд дискретных значений аргумента x₁, x₂. x_n и соответствующих им значений функции y₁, y₂. y_n задаются в виде таблицы.

Пример.Различные статистические и социологические данные записывают в виде таблиц: уровня жизни, динамики безработицы, численности населения и т.п.

Третьим способом задания функции является графический способ .

Абсциссой x точки (x;y) на плоскости xOy называется длина отрезка [O;x] , отсекаемого от точки отсчета O оси Ox плоскости. Ординатой этой точки называется длина отрезка [O;y] оси Oy плоскости xOy .

Графиком функции y=f(x) называется множество точек (x;y) на плоскости xOy (геометрическое место точек на плоскости), каждая из которых обладает тем свойством, что ее абсцисса есть значение аргумента функции, а ордината — соответствующее этому аргументу значение функции. Графически функция определяется обычно в экспериментальных науках, например, в разделах физики, химии.

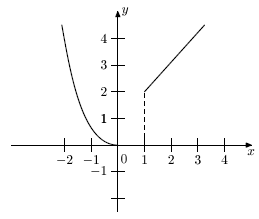
Пример. График кусочно-заданной на интервале (-2;3) функции f(x) , приведенной выше, будет иметь вид, изображенный рис. 4.1. Хотя этот график и состоит из трех «вроде бы» самостоятельных частей (часть параболы ; часть оси Ox ; часть прямой , параллельной биссектрисе координатного угла), тем не менее, это один график ( график одной кусочно-заданной функции). График функции может не быть непрерывной линией. При x=1 указанный на рис. 4.1. график теряет свойство быть непрерывным. Функция имеет при x=1 разрыв (о разрывах функции мы подробнее поговорим ниже).

При словесном задании функции словесно указываются множества X , Y и закон f .

Пример. Функция Дирихле, рассмотренная нами выше, была определена словесно, так как значения из множеств X , Y — «словесны, расплывчаты».

Если задана некоторая однозначная функция 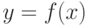, , , то каждому значению ставится в соответствие только одно значение . Если при этом каждому значению соответствует лишь одно значение , то говорят, что отображение f есть взаимно однозначное отображение .

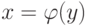
Так как каждому в этом случае ставится в соответствие одно значение , то можно говорить, что определена функция 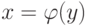вида с областью определения и областью значений .

Функция называется функцией, обратной к (прямой) функции y=f(x) . Обратную к f функцию g часто обозначают f_-1 (g=f_-1) .

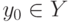
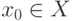
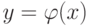
Если дана функция y=f(x) и для любого значения уравнение f(x)=y₀ имеет единственный корень , то функция y=f(x) обратима. Если функция определена и возрастает (убывает) на промежутке X , то у нее существует обратная функция , причем обратная функция определена и возрастает (убывает) на Y . Таким образом, график обратной функции симметричен с графиком данной функции y=f(x) относительно биссектрисы первого и третьего координатных углов.

Пример. Функция y=x 2 с областью определения D(f)=R , областью изменения и функция не является взаимно однозначной, а функция y=x 3 с обратной однозначной функцией — взаимно однозначная.

Пусть дано некоторое соотношение, связывающее две переменные x и y . Если все его члены перенести в левую часть, то оно запишется в виде: F(x,y)=0 . Если существуют различные пары действительных чисел (x,y) , удовлетворяющих данному соотношению, то соотношение F(x,y)=0 можно считать способом задания переменной y как функции от x . С помощью этого соотношения каждому значению ставится в соответствие (фиксируем каждый раз x , решаем, при фиксированном x , уравнение и находим y ). Функция от x , определяемая соотношением F(x,y)=0 , называется неявно заданной функцией .

Пример.Соотношение 2x-y+1=0 неявно задает y как функцию от x ; эту функцию можно выразить явно, разрешив уравнение относительно y : y=1+2x . Соотношение x 2 +y 2 -1=0 неявно задает двухзначную функцию 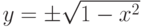; уравнение задает неявную функцию y (не выражаемую явно через x ).

Функция f(x) называется четной , если f(x)=f(-x) для всех , где X — область определения функции y=f(x) . График четной функции симметричен относительно оси Oy . Функция называется нечетной , если f(x)=-f(-x) , для любого . График нечетной функции симметричен относительно начала координат. Области определения четной и нечетной функции симметричны относительно начала координат. Функция может быть ни нечетной, ни четной.

Пример. Функция y=x 2 cos(x) — четная, так как y(-x)=(-x) 2 cos(-x)= x 2 cos(x)=y(x) , а функция y=x 2 sin(x) — нечетная, так как y(-x)=(-x) 2 sin(-x)=-x 2 sin(x)=-y(x) . Функция y=x+2 не является ни четной, ни нечетной, так как y(-x)=-x+2 .

Источник

Функция. Способы задания функций.

Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.

1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.

Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.

2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.

Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.

Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.

4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.

Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.

5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.

При разложении числа Эйлера задается функцией:

Ее сокращение приведено ниже:

При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.

Источник