Графическое решение неравенств
Приближённое решение неравенств.
Графическое решение неравенств с одним неизвестным.
Графическое решение систем неравенств с двумя неизвестными.
Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными. Чтобы решить графически неравенство с одним неизвестным, необходимо перенести все его члены в одну часть, т. e . привести к виду:
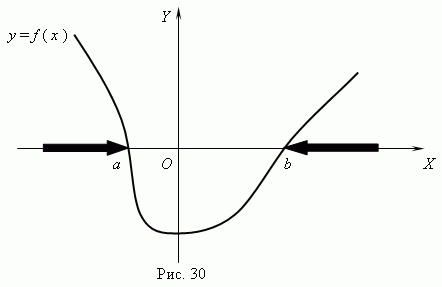
и построить график функции y = f ( x ). После этого, используя построенный график, можно найти нули функции (см. выше), которые разделят ось Х на несколько интервалов. Теперь на основе этого определим интервалы x , внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции: a и b ( рис.30 ). Тогда из графика очевидно, что интервалы, внутри которых f ( x ) > 0: x a и x > b ( они выделены жирными стрелками ). Ясно, что знак > здесь условный; вместо него может быть любой другой:
Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т. e . привести неравенства к виду:
и построить графики функций y = f ( x ), y = g ( x ) , . , y = h ( x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т. e . их общую часть.
П р и м е р . Решить графически систему неравенств:
Р е ш е н и е . Сначала построим графики функций y = — 2 / 3 x + 2 и
Решением первого неравенства является интервал x > 3, обозначенный на рис.31 чёрной стрелкой; решение второго неравенства состоит из двух интервалов: x — 1 и x > 1, обозначенных на рис.31 серыми стрелками.
Из графика видно, что пересечением этих двух решений является интервал x > 3. Это и есть решение заданной системы неравенств.
Чтобы решить графически систему двух неравенств сдвумя неизвестными, надо:
1) в каждом из них перенести все члены в одну часть, т. e . привести
нера венства к виду:
2) построить графики функций, заданных неявно: f ( x , y ) = 0 и g ( x , y ) = 0;
3) каждый их этих графиков делит координатную плоскость на две части:
в одной из них неравенство справедливо, в другой – нет; чтобы решить
графически каждое из этих неравенств, достаточно проверить
справедливость неравенства в одной произвольной точке внутри любой
части плоскости; если неравенство имеет место в этой точке, значит
эта часть координатной плоскости является его решением, если нет – то
решением является противоположная часть плоскости ;
4) решением заданной системы неравенств является пересечение
(общая область) частей координатной плоскости.
П р и м е р . Решить систему неравенств:
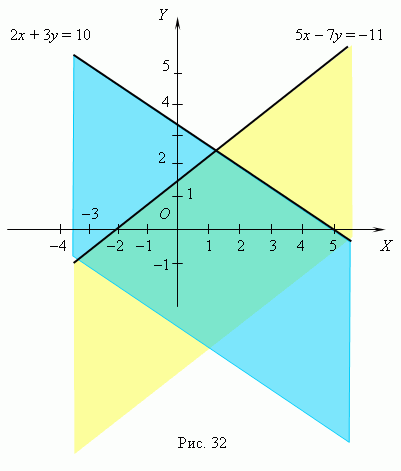
Р е ш е н и е . Сначала строим графики линейных функций: 5 x – 7 y = — 11 и
2 x + 3 y = 10 ( рис.32 ). Для каждой из них находим полуплоскость,
внутри которой соответствующее заданное неравенство
справедливо. Мы знаем, что достаточно проверить справедливость
неравенства в одной произвольной точке области; в данном
случае легче всего использовать для этого начало координат O ( 0, 0 ).
Подставляя его координаты в наши неравенства вместо x и y ,
получим: 5 · 0 – 7 · 0 = 0 > — 11, следовательно, нижняя
полуплоскость ( жёлтого цвета ) является решением первого
неравенства; 2 · 0 + 3 · 0 = 0 неравенство
имеет своим решением также нижнюю полуплоскость ( голубого
цвета ). Пересечение этих полуплоскостей ( область цвета бирюзы )
является решением нашей системы неравенств.
Copyright © 2004 — 2007 Др. Юрий Беренгард. All rights reserved.
Источник
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
| x | y |
| 0 | -1 |
| 1 | 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Источник

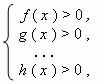
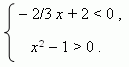
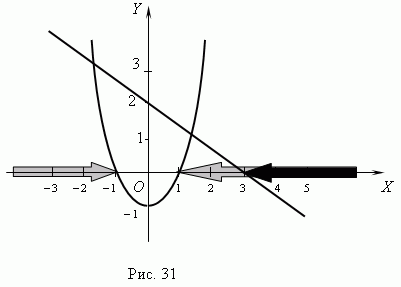
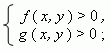
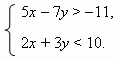






 при х ≠ -1.
при х ≠ -1.






 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0. , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b 



























