Что значит механический способ

Механическая память — примитивная зубрёжка или база для успешного обучения?

На протяжении многих лет в психологии не утихают споры о том значении, которое имеет механическая память в жизни человека. Одни считают её слишком примитивной формой, работающей в рамках первой сигнальной системы (которая имеется и у некоторых животных). Другие склонны считать её той базой, без которой было бы сложно осваивать определённые типы материала, не подвластного логике и осмыслению. Так или иначе, но без неё, действительно, бывает трудно в определённые моменты, и поэтому её развитию нужно уделять не меньшее внимание, чем всем остальным видам памяти.

Что это такое

Механическая память — это способность запоминать и воспроизводить информацию такой, как она есть, без осмысления и включения в работу логических связей, то есть автоматически заучивать её посредством многократных повторов. Сокращённое название — МП. Не является показателем интеллекта. Основана на нейронных связях, формирующихся в рамках первой сигнальной системы (I с. с.).

Последовательное запоминание блоков информации происходит по принципу, который в психологии носит название «ассоциаций по смежности». Это значит, что слова фиксируются в памяти точно в таком виде, в каком человек их увидел, услышал или произнёс. Нельзя сказать, что при этом их смысл вообще не усваивается и полностью теряет своё значение, но он становится второстепенным.

Основной приём запоминания — многократное повторение. Оно заключается в максимально точном воспроизведении информации в виде образов, формирующихся в I с. с. Закрепление нужных нейронных связей в ней является результатом суммарного количества репетиций. Некоторые называют это зубрёжкой.

Пример. Запоминание и воспроизведение такой информации, как:

• имена;
• географические названия;
• числа;
• иностранные слова;
• номера телефонов;
• сложные термины;
• стихотворения;
• формулы.

В психологии это полная противоположность логической (смысловой) памяти.

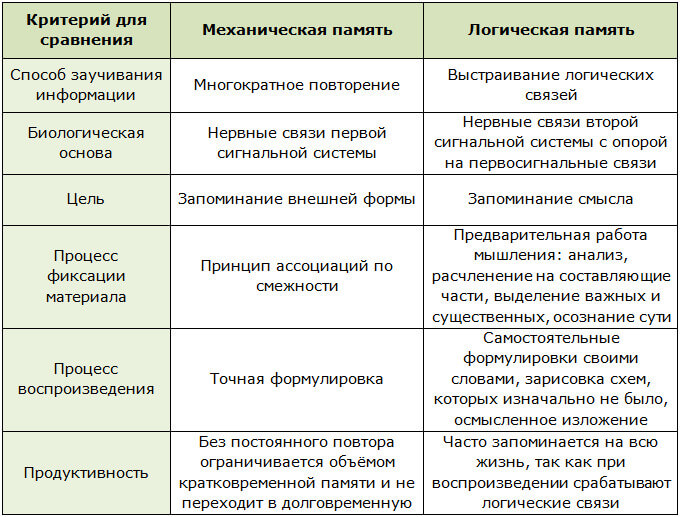
Механическая VS логическая

В общей классификации механическая и логическая память различаются в основном по способам (приёмам) заучивания информации. Однако это не единственный критерий, по которому их можно сравнивать.

Особенно важны оба вида в период обучения для школьников и студентов, которым требуется заучивать огромный объём учебного материала. Поэтому на разных возрастных этапах проводится психологическое исследование логической и механической памяти, чтобы выяснить, какая из них преобладает, и оптимально использовать это в учебном процессе.

Если у ребёнка в начальной школе преобладает механическая память, это не является проблемой. Однако такой результат тестирования — сигнал для родителей и преподавателей, чтобы делали упор на развитие логической. Нужно научить его выстраивать смысловые связи и использовать их для запоминания нужной информации. В дальнейшем это облегчит ему процесс обучения.

А вот преобладание механической памяти в подростковом возрасте — это уже серьёзная проблема. Это ещё не патология, но уже далеко не норма. Дети, у которых отмечается такой перевес, подчас даже являются отличниками. Но именно они сидят за уроками большую часть своего времени, что приводит к синдрому хронической усталости. На этом фоне развивается вегетососудистая дистония: скачки давления, кровь из носа, головные боли, частые инфекции. А всё потому, что объёмы учебного материала в старших классах огромны, и для его механического заучивания без осмысления требуется большое количество времени. Поэтому так важно, чтобы у ребёнка были развиты оба вида памяти.

Характеристика

Механическая память характеризуется следующими особенностями:

• она всегда произвольная, то есть осуществляется сознательно, имеет цель (выучить конкретный материал), использует для её достижения специальный приём (многократное повторение), требует наличия волевых усилий;
• чаще всего она вербальная (заучиваются именно слова) — в отношении движений, запахов, мелодий действует больше процесс приобретения профессиональных навыков;
• она кратковременная: если стихотворение или новое иностранное слово не повторять, они забудутся;
• её объёмы ограничены: за 1 раз каждый человек может выучить только определённое количество слов, формул, четверостиший.

Механическая память также характеризуется тем, что совершенно не пластична. Если изначально, используя её, человек запомнил искажённую информацию с ошибками, впоследствии он воспроизводит её так же, потому что не осознаёт неправильность. В качестве примера можно привести изучение иностранного языка. Если сразу заучить слова в неправильной транскрипции, в дальнейшем такое произношение прочно закрепится в коре больших полушарий, с рецепторами которых связана МП, и переучиться будет гораздо труднее, чем сразу выучить всё правильно.

Примитивная и непластичная форма МП подтверждается многочисленными экспериментами. Если хоть немного изменить условия воспроизведения информации, которая была заучена таким способом, человек с трудом выполняет данное ему задание. Например, если его попросят рассказать стихотворение, поменяв в нём места четверостиший, или заменить в формуле какое-то одно из значений, или выставить на тренажёре другие настройки. Результат будет один и тот же — ошибки и постоянные заминки.

Все вышеперечисленные особенности должны учитываться преподавателями во время обучения. Нельзя давать ребёнку слишком большие объёмы материала для автоматического заучивания. Чтобы гармонично развить оба вида памяти (и механическую, и логическую), необходимо:

• научить ребёнка ставить перед собой цель в соответствии с задачей, которую дал учитель (выучить формулу/стихотворение/слова по-английски);
• помочь ему в освоении приёма многократных повторений (чтобы запомнить материал не за 10 раз, а за 2-3);
• тренировать силу воли;
• развивать вербальную систему восприятия;
• научить переводить МП из кратковременной в долговременную путём постоянного повторения заученного материала.

Постепенно, в процессе обучения, начиная с начальной школы, необходимо развивать у ребёнка логическую память, чтобы она к 10-11 годам преобладала над механической. Но забрасывать последнюю тоже не стоит. Обе играют разные, но важные роли в становлении и формировании полноценной и успешной личности.

Диагностика

Методика «Определение коэффициента логической и механической памяти»

В начальной школе и в подростковом возрасте психологом проводится тест, какая память преобладает у ребёнка — механическая или логическая. Это необходимо для выстраивания правильной методики обучения с учётом индивидуальных особенностей.

Цель: выяснение уровня развития и соотношения ЛП и МП у учеников начальной школы.

Возраст: 7-10 лет (для подростков подбираются другие словесные пары).

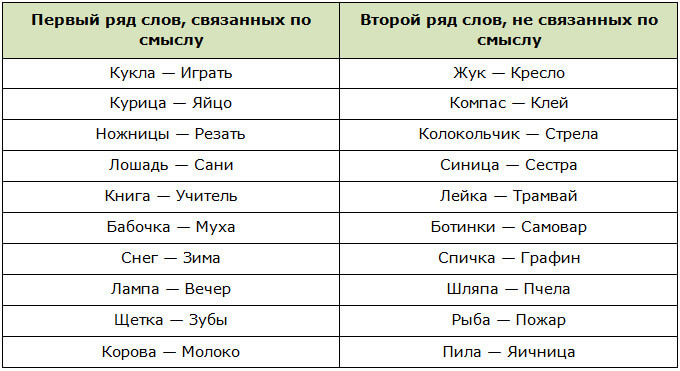
Оборудование: листы бумаги на каждого ученика, секундомер (часы), ряды и пары слов.

1. Постановка задачи перед ребёнком: запомнить пары слов, которые ему зачитают.
2. Прочтение первого словесного ряда с 5-секундным интервалом между каждой парой.
3. Десятисекундный перерыв.
4. Прочтение первых слов каждой пары с интервалом в 10-15 секунд. Ребёнок в это время записывает вторые слова пар.
5. Тот же алгоритм — со вторым рядом.

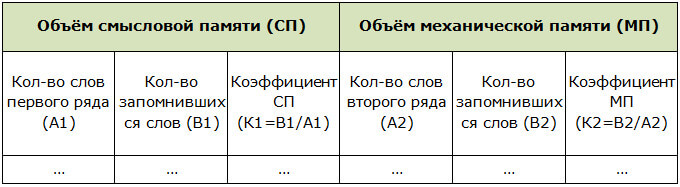
По результатам составляется таблица:

Диагностика заболеваний

Гипомнезия — нарушение механической памяти, когда логическая продолжает работать, а вот элементарные вещи не фиксируются. Даже взрослый человек может просидеть над текстом небольшого объёма часа 3 и совершенно ничего не запомнить. Она бывает временной, если причина — хроническая усталость или сильный стресс. Всё гораздо хуже, когда она носит хронический характер и свидетельствует о необратимых процессах в гипокампе. Такое состояние требует неотложного лечения и правильной дифференциальной диагностики, включающей в себя:

• тестирование (метод 10 слов, пиктограммы, работа с текстом);
• ЭЭГ, КТ, МРТ, ЭКГ;
• анализы крови и мочи (для выявления заболеваний, спровоцировавших гипомнезию).

Задача дифференциальной диагностики — не спутать гипомнезию с прочими заболеваниями, так как её клиническая картина похожа на симптомы, сопровождающие неврозы и депрессию.

Особый случай

Серьёзные нарушения диагностируются у детей с ЗПР. С помощью словесных проб Лурии у них были выявлены следующие особенности:

• МП хуже, чем у обычных школьников, но лучше, чем у олигофренов;
• общее количество попыток заучивания близко к норме;
• возникает мощная интерференция (и ретроактивная, и проактивная), что приводит к торможению нейронных связей;
• ребёнок запоминает первый блок информации, но при заучивании следующего стирается первый;
• на результаты сильно влияет наличие помех (отвлекающие факторы).

Психологи утверждают, что у детей с ЗПР успешность механического запоминания напрямую зависит от организации процесса заучивания.

Развитие

Хорошая механическая память может быть врождённой (так как связана с I с. с.) и приобретённой. Первая обусловлена высокой гибкостью нервной системы. При такой способности выучить материал получается уже после 1-2 повторений. Часто это обнаруживается у полиглотов.

Однако не нужно расстраиваться, если вы не являетесь обладателем такого феномена. Во-первых, информацию всегда можно заучить через многократное её повторение. Это укрепляет изначально слабые нервные связи, так как прокладываются необходимые сигнальные пути между участками полушарий, отвечающими за фиксацию и воспроизведение данного материала.

Во-вторых, всегда можно развить механическую память, сделать так, чтобы её объём увеличился. Психологи предлагают использовать для этого следующие приёмы:

• активное изучение иностранных языков;
• заучивание стихов наизусть, постепенно увеличивая их объёмы: от четверостиший к поэмам;
• запоминание математических формул и сложных научных терминов;
• постепенное устранение списков: учите наизусть продукты, которые нужно купить, номера телефонов и адреса, имена и отчества людей;
• методика ночного запоминания: прочитать нужную информацию перед сном и повторить её сразу после пробуждения наутро.

Несмотря на то, что механическая память по многим показателям проигрывает логической, она является базой успешного процесса обучения. Поэтому нужно следить за её полноценным развитием с раннего детского возраста.

Источник

Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Механический способ

Механический способ определения площади – это измерение на карте или плане площади участка с произвольными границами при помощи специального прибора – планиметра. Полярный планиметр имеет два рычага: полюсный R1 и обводной R (рис.6.4).

Один конец полюсного рычага – точка 0 – является полюсом планиметра, – на нем крепится игла; другой его конец шарнирно соединяется с обводным рычагом в точке b. На одном рычаге обводного рычага имеется счетное колесо K, которое располагается перпендикулярно рычагу, на другом конце рычага находится обводная точка f. Для механического счета числа оборотов счетного колеса имеется счетный механизм. Счетный барабан разделен на сто частей,и сбоку от него имеется верньер на одну десятую деления. Обводное колесо и счетный механизм помещаются на каретке, которую можно перемещать вдоль обводного рычага , изменяя тем самым его длину R = bf.

Измерение площади сводится к обводу по контуру участка на карте обводной точкой f; при этом вследствие трения о бумагу счетное колесо вращается. Берут отсчет по счетному механизму до обвода контура n1 и после обвода – n2. Площадь участка вычисляют по формуле:

P = c * ( n2 – n1 ), (6.21)

где c – цена деления планиметра.

Внешний вид полярного планиметра изображен на рис.6.5; на нем цифрами обозначены: 1 – основная каретка, 3 – полюсный рычаг, 4 – полюс, 6 – стеклянная пластинка с обводной точкой, 7 -обводной рычаг, 8 – шарнирное соединение, 9 – счетчик полных оборотов, 10 – счетное колесо, 11 – верньер.

Теория полярного планиметра. Предметом теории планиметра является вывод формулы площади обводимого участка в зависимости от числа оборотов счетного колеса. При выводе формулы выделим два случая: полюс планиметра располагается внутри контура и вне контура.

Рассмотрим первый случай – полюс внутри контура. Обозначим:
R – длина обводного рычага,
R1 – длина полюсного рычага,
r -расстояние от счетного колеса до шарнира (рис.6.6).

Пусть обводная точка f движется по контуру участка и в какой -то момент занимает положение f1.

Через малый промежуток времени она займет положение f2, а точка b переместится из положения b1 в положение b2. За этот промежуток времени планиметр измерит площадь pi элементарного участка; на рисунке этот участок заштрихован. Площадь pi можно представить как сумму площадей трех фигур:

параллелограмма b1b2f’1f1 – R*hi,
кругового сектора Ob1b2 радиуса R1 – 0.5 * R12 * αi;
кругового сектора b1f’1f2 радиуса R – 0.5 * R2*β i;

Источник

Механическое движение и его характеристики

теория по физике 🧲 кинематика

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

• Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
• Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
• Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.

По типу линии, вдоль которой движется тело, выделяют два вида движения:

• Прямолинейное — тело движется по прямой линии.
• Криволинейное — тело движется по кривой линии, в том числе замкнутой.

По скорости выделяют два вида движения:

• Равномерное — скорость движущегося тела остается неизменной.
• Неравномерное — скорость движущегося тела с течением времени меняется.

По ускорению выделяют три вида движения:

• Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
• Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
• Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

• Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
• Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
• Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.

Способы описания механического движения

Описать механическое движение можно двумя способами:

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

Перемещение

Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S .

Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δ r . С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

В физике скорость обозначается V . Математически скорость определяется формулой:

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

В физике ускорение обозначается a . Математически оно определяется формулой:

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

• Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
• Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.

Внимание!

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Алгоритм решения

1. Записать исходные данные в определенной системе отсчета.
2. Записать формулу ускорения.
3. Выразить из формулы ускорения скорость.
4. Найти искомую величину.

Решение

Записываем исходные данные:

• Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v₀ = 0 м/с.
• Ускорение, с которым тело начинает движение, равно: a = 4 м/с 2 .
• Время движения согласно условию задачи равно: t = 2 c.

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид :

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник