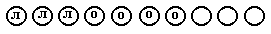Что такое второй способ решения задач

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

пойманных рыб: л — лещи, о — окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

1) 3 + 4 = 7 (р.) — пойманные рыбы

Для ответа на вопрос задачи мы выполнили два действия.

Пусть х — пойманные щуки

Тогда количество всех рыб можно записать выражением:

3 + 4 + х — все рыбы

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

Читайте также: Единственно верный способ общения это
1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Как решать логические и математические задачи

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день. На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.

Решаем логические задачи

Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.

Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.

К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями.

Более сложными и увлекательными типами заданий являются задачи, в которых отдельные утверждения являются истинными, а другие ложными. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры широкого ряда нестандартных задач на логику.

Основные методы решения логических задач

метод рассуждений;

с помощью таблиц истинности;

метод блок-схем;

средствами алгебры логики (алгебры высказываний);

графический (в том числе, «дерево логических условий», метод кругов Эйлера);

метод математического бильярда.

Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):

метод последовательных рассуждений;

разновидность метода рассуждений — «с конца»;

табличный способ.

Метод последовательных рассуждений

Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.

На столе лежат Голубой , Зеленый , Коричневый и Оранжевый карандаши.

Третьим лежит карандаш, в имени которого больше всего букв. Голубой карандаш лежит между Коричневым и Оранжевым .

Разложи карандаши в описанном порядке.

Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.

Больше всего букв в слове «коричневый», значит, он лежит третьим.

Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.

Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.

Для зеленого карандаша осталась последняя позиция — он лежит четвертым.

Метод «с конца»

Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.

Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.

Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?

Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.

Читайте также: Способ подачи сигнала сос
Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.

Решение логических задач с помощью таблиц истинности

Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».

Три спортсмена ( красный , синий и зеленый ) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».

Кто забросил мяч, если только один из троих сказал неправду?

Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.

Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.

Рассмотрим первый вариант ответа («мяч забросил красный «), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный «), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый ) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый « — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.

И, наконец, третий вариант: предположим, что «мяч забросил синий «.
Тогда утверждение «мяч забросил синий « — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.

Значит, правильный ответ – мяч забросил синий.

Метод блок-схем

Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.

графически (блок-схемой) описываем последовательность выполнения операций;

определяем порядок их выполнения;

в таблице фиксируем текущие состояния.

Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.

Отгадывайте самые интересные загадки на логику, собранные специально для постоянных читателей нашего блога и учеников LogicLike, решайте логические задачи онлайн вместе с тысячами детей и взрослых!

Учим детей 5-12 лет решать любые логические и математические задачи. Более 3500 занимательных заданий с ответами и пояснениями.

Источник

Различные способы решения задач и различные формы записи решения

Страницы работы

Содержание работы

С. Е. ЦАРЕВА. Различные способы решения задач и различные формы записи решения// Начальная школа, 1982. — №2. – с.39-41.

На одном из уроков математики во II классе ученик, получив задание “Реши задачу”, спросил: “Каким способом нужно решать: по действиям или выражением”. Учитель ответил: “По действиям”.

Этот диалог показал, что и учитель, и ученик принимают различные формы записи решения за различные способы ее решения. Посещение уроков, беседы с учителями и учащимися позволили нам сделать вывод, что эта ошибка довольно распространена. Смешение же названных понятий приводит к тому, что, когда требуется действительно решить задачу разными способами, учащиеся либо вовсе не понимают задания, либо понимают его с большим трудом. А это, в свою очередь, снижает обучающие и воспитывающие возможности такого важного вида работы над задачей, как решение задач разными способами.

Поэтому мы считаем своевременным обратить внимание учителей на отличие понятий способа решения задачи и формы записи решения задачи.

Задача считается решенной различными способами, если се решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.

Читайте также: Наиболее простые способы дезинтоксикационной терапии
Рассмотрим, например, задачу № 522 из учебника математики для II класса: “Для уроков труда купили 4 катушки белых ниток, по 10 коп. за катушку, и 6 катушек черных ниток по такой же цене. Сколько денег уплатили за эти нитки?”

Эта задача может быть решена двумя арифметическими способами.

При первом из них, наиболее очевидном, первоначально определяют стоимость черных ниток: (10-4)-коп., затем стоимость белых ниток: (10-6) коп. и, наконец, стоимость всех ниток.

При втором способе замечаем, что цена 1 катушки белых ниток та же, что и черных, поэтому вначале можно узнать, сколько всего катушек ниток купили (6+4), а затем определить стоимость всех этих ниток

Запись решения, для каждого способа может быть выполнена в нескольких формах. Покажем все эти формы для каждого способа решения.

Запись решения по действиям с планом.

1. Сколько стоят белые нитки? 10·4 = 40 (коп.)

2. Сколько стоят черные нитки? 10·6=60 (коп.)

3. Сколько денег уплатили за все эти нитки?

1. Сколько всего катушек с нитками купили?

2. Сколько денег уплатили за все эти нитки?

В настоящее время эта форма записи решения задач в начальной школе практически не применяется. Однако мы считаем, что ознакомить с ней учащихся полезно и ее можно использовать на уроках математики, хотя и значительно реже, чем другие формы.

Рассмотрим другую форму записи решения той же задачи — это запись решения по действиям с пояснениями.

1. 10 · 4 =40 (коп) — стоимость белых ниток,

2. 10 ·6 = 60 (коп) — стоимость черных ниток.

3. 40+60=100 (коп.) — стоимость всех ниток.

4. 100 коп.= 1 руб.

1. 6+4 = 10 (шт.) — всего купили катушек ниток.

2. 10·10 = 100 (коп) — стоимость всех ниток.

3. 100 коп. = 1 руб.

Решение задачи можно также оформить по действиям без пояснений.

3. 40 + 60=100 (коп).

4. 100 коп. = 1 руб.

2. 10 · 10=100 (коп).

3. 100 коп.= 1 руб.

Ответ: все нитки стоят 1 руб.

Ответ: все нитки стоят 1 руб.

По задаче можно также составить выражение и найти его значение.

10 · 4+10 · 6=100 (коп)

Ответ: все нитки стоят 1 руб

Ответ: все нитки стоят 1 руб.

Запись решения в этой форме осуществляется учащимися в два этапа. Вначале составляется выражение, затем учащиеся находят его значение, после чего запись решения приобретает вид равенства, в левой части которого записано выражение, составленное по задаче, а в правой части — его значение.

Ни в коем случае нельзя называть запись 10 · 4 + 10 · 6 = 100 выражением, так как это противоречит тому определению понятия выражения, которое положено в основу изучения этого понятия в школе. Математическое выражение составляется из цифр, букв, знаков арифметических действий и скобок, но не содержит знаков математических отношений: равенства, неравенства и др. Два математических выражения, соединенные знаком равенства, образуют равенство.

Приведенная выше запись — это равенство, левая часть которого есть выражение, составленное по задаче (10 · 4 + 10 ··6), а правая часть — выражение, состоящее всего лишь из одного числа (100), являющегося значением предыдущего выражения.

При проверке решения задачи, записанной в этой форме, учащимся можно дать такие задания:

1. Прочитайте выражение, составленное по задаче.

При выполнении этого задания учащиеся должны прочитать только левую часть равенства. (Сумма двух произведений 10·4 и 10·6.) После чтения выражения можно задать вопросы, ответы на которые покажут, как учащиеся понимают смысл каждой части выражения (10 — 4 и 10 — 6) и всего выражения в целом (10 · 4 +10 · 6): что означает произведение десяти и четырех? десяти и шести? что означает сумма этих произведений?

2. Назовите значение этого выражения. (Значение составленного по задаче выражения равно 100.)

3. Дайте ответ на вопрос задачи. (Все нитки стоят 100 коп., т. е. 1 руб.)

При решении задач следует правильно употреблять в своей речи соответствующие термины: Решите задачу и запишите решение по действиям с пояснениями. Решите задачу двумя способами, записав каждое решение в виде равенства, левая часть которого — выражение, составленное по задаче. Решите задачу двумя способами. Составьте соответствующие выражения и найдите их значения. Решите задачу и запишите решение вначале по действиям с пояснениями, а затем в виде выражения. Найдите значение этого выражения. Дайте ответ на вопрос задачи.

Источник