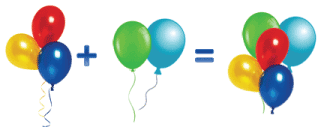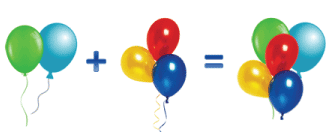Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
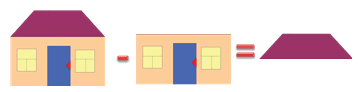
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 — 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 — первое слагаемое
2 — второе слагаемое
2 + 3 = 5
2 — первое слагаемое
3 — второе слагаемое
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = . (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
37 + 30 = 67, значит,
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Источник
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения
Перечень вопросов, рассматриваемых в теме:
— Что такое сочетательное свойство сложения?
-В каких случаях можно использовать свойства сложения?
Глоссарий по теме:
Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.
Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47
2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19
3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29
Теоретический материал для самостоятельного изучения
Сравним выражения и их значения:
Сумма чисел шесть и девять равна сумме чисел девять и шесть.
Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.
Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?
Правильно, оно называется переместительным свойством сложения.
В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?
Первый способ решения.
Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.
Второй способ решения.
Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.
В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)
Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.
Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.
Решим выражение: 1+7+9+3=?
Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.
В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.
Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.
1. Вычислите суммы удобным способом
30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________
1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)
2. Совместите название математического свойства с его значением и выражением
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Источник
Свойства сложения и вычитания
О чем эта статья:
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
- 2 — это первое слагаемое,
- 5 — второе слагаемое,
- 7 — это сумма.
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
- Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a - Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c) - Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.
Рассмотрим пример 9 — 4 = 5, в котором:
При этом саму запись (9 — 4) тоже можно назвать разностью.

Примеры использования свойств сложения и вычитания
Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:
Пример 1
Вычислить сумму слагаемых с использованием разных свойств:
а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15
б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22
в) 30 + 0 + 13 = 30 + 13 = 43
Пример 2
Применить разные свойства при вычислении разности:
а) 25 — 0 — 2 = 25 — 2 = 23
б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13
Пример 3
Найти значение выражения удобным способом:
а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32
б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16
Источник
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения
Перечень вопросов, рассматриваемых в теме:
— Что такое сочетательное свойство сложения?
-В каких случаях можно использовать свойства сложения?
Глоссарий по теме:
Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.
Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47
2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19
3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29
Теоретический материал для самостоятельного изучения
Сравним выражения и их значения:
Сумма чисел шесть и девять равна сумме чисел девять и шесть.
Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.
Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?
Правильно, оно называется переместительным свойством сложения.
В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?
Первый способ решения.
Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.
Второй способ решения.
Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.
В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)
Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.
Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.
Решим выражение: 1+7+9+3=?
Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.
В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.
Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.
1. Вычислите суммы удобным способом
30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________
1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)
2. Совместите название математического свойства с его значением и выражением
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Источник