Что такое табличный способ решения логических задач

Решение логических задач с помощью таблиц
учебно-методический материал по информатике и икт (7 класс) на тему

Данный материал можно использовать в 7 классе при изучении темы «Решение логических задач с помощью таблиц» . Материала позволяет расширить представления учащихся о табличных информационных моделях, закрепить представление о табличном способе решения логических задач, закрепить навыки создания таблиц

Скачать:

Вложение	Размер
zadachi_tablichnye.docx	25.66 КБ

Предварительный просмотр:

Учебно-методическое пособие.»Табличное решение логических задач. 7 класс»

Напрушкина Е.С. учитель математики и информатики ГБОУ СОШ№136.

Вся наша жизнь это непрерывное решение больших и маленьких логических проблем. Без умения логически думать, рассуждать, делать выбор жить трудновато.

Основной смысл в решении логической задачи состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами. В первую очередь, логика отвечает за упорядочивание мыслей. Отсюда можно сказать, что логические задачи – задачи, в первую очередь, на установление порядка

В данном пособие рассматривается прием, который используется при решении текстовых логических задач, — построение таблиц . Таблицы помогают делать правильные логические выводы в ходе решения задачи и позволяют наглядно представить условие задачи или ее ответ.

Но этот прием не обладает универсальностью, т.к. предназначен для решения только одного типа задач. Построение таблицы требует анализа находящейся в ней информации, умения сравнивать и сопоставлять.

Первый шаг решения задачи — это специально составленная таблица .
Далее в таблице отражается условие задачи. Ячейки таблицы заполняются цифрами 0 и 1 в зависимости от того, ложно («0») или истинно («1») соответствующее высказывание.

В данной разработке представлены задачи, решаемые табличным способом. Учащиеся могут решать задачи как с помощью ПК, так и в тетрадях. Всего представлено 10 задач, учащиеся сами выбирают 3 задачи, которые они могут решить,

В одном дворе живут четыре друга. Вадим и шофёр старше Сергея; Николай и слесарь занимаются боксом; электрик – младший из друзей; по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.

Источник

Решение логических задач табличным способом

Главным в предлагаемых задачах является способ решения — построение таблицы, строки которой соответствуют элементам одного из рассматриваемых в условии задачи множеств, столбцы — элементам другого, пересечение строки и столбца — комбинации двух элементов разных множеств. С помощью такой таблицы анализируются условия задачи, делаются выводы, проверяется избыточность, полнота и правильность выводов.

Задача 1. После соревнований бегунов на табло появилась надпись:
• Рустам не был вторым.
• Эдуард отстатл от Рустама на два места.
• Яков не был первым.
• Галина не была не первой ни последней.
• Карина финишировала сразу за Яковом.
Кто же победил в этих соревнованиях? Каково было распределение бегунов на финише?

Решение:
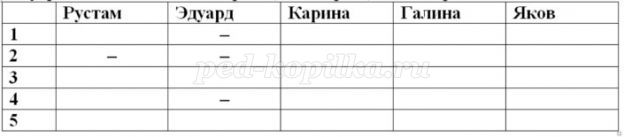
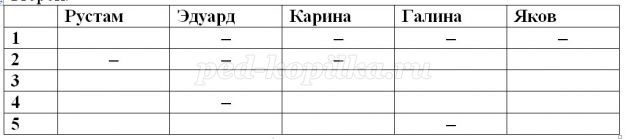
Рисуем таблицу, где столбцы –имена детей, а строки – номера мест. Читаем задачу, пошагово анализируем условие и ставим в таблицу «+», если соответствие установлено и «–», если точно соответствия нет.
Так как Рустам не был вторым и Эдуард отстал от Рустама на два места, то Эдуард не может быть ни первым, ни вторым, ни четвёртым.

Так как Карина финишировала сразу за Яковом, то очевидно, что Яков был четвёртым, а Карина последней и тогда Галина была второй.

Итак, можно выделить
Пять простых шагов на пути поиска решения логических задач.
1. Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты.
2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов.
3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок.
4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия.
5. Решение можно найти простым методом последовательных исключений.

Чем больше будете тренироваться, тем лучше у вас это будет получаться. А теперь за дело.

Задача 2.
В субботний вечер Семен, Коля и Витя решили развлечься. У них был выбор: кино, рок-концерт или танцы.
• Семён любит кино, но к танцам менее нетерпим, чем к рок-музыке.
• Коля любит танцевать, но готов пойти в кино скорее, чем на рок концерт.
• Витя любит рок-музыку меньше чем танцы, но кино ему всё-таки не так неприятно, как танцы или концерт.
Поскольку вопрос решатся большинством голосов, то куда, на ваш взгляд отправились эти ребята?
Задача 3.
Трое мальчиков Костя, Фома и Марат дружили с тремя девочками – Женей, Светой и Мариной. Но вскоре компания разделилась на пары, потому, что оказалось:
• Света ненавидит ходить на лыжах.
• Костя, Женин брат часто катается со своей подружкой на лыжах
• А Фома теперь бежит на свидание к Костиной сестре.
С кем же проводит время Марат?

Задача 4.
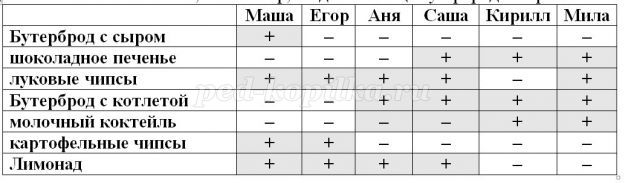
Шестеро друзей в ожидании электрички заскочили в буфет.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад.
Из чего состоял завтрак каждого из друзей?

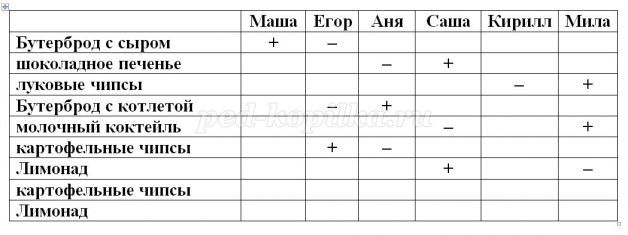
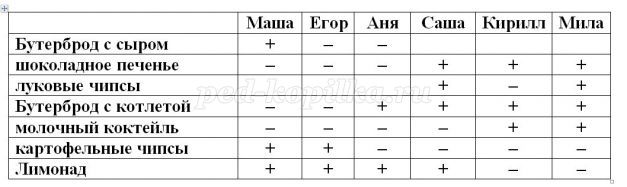
Решение: Так как
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром;
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье;
• Кирилл ел то же, что и Мила, но без луковых чипсов;
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы;
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то:

Задача 5.
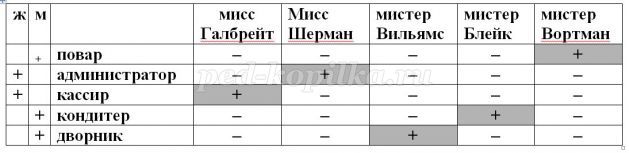
В одном небольшом кафе в смене одновременно работали 5 человек: администратор, повар, кондитер, кассир, дворник. Одновременно на работу выходили мисс Галбрейт, мисс Шерман, мистер Вильямс, мистер Вортман и мистер Блейк. При этом известно, что:
1. Повар – холостяк.
2. Кассир и администратор жили в одной комнате, когда учились в колледже.
3. Мистер Блейк и мисс Шерман встречаются только на работе.
4. Миссис Вильямс расстроилась, когда муж сказал ей, что администратор отказал ему в отгуле.
5. Вортман собирается быть шафером на свадьбе у кассира и кондитера.
Кто на какой должности в этом кафе?

Можно разделить учащихся на группы и каждой группе дать индивидуальное задание или подобрать задачи для каждого ученика.

Задача 1.
Коля, Боря, Вова и Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они ответили:
1) «Коля не занял ни первое, ни четвертое места».
2) “Боря занял второе место”.
3) “Вова не был последним”.
Какое место занял каждый мальчик?
Задача 2.
Три одноклассника — Влад, Тимур и Юра встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой — физиком, а третий — юристом. Один увлекся туризмом, другой — бегом, третий — регби.
1. Юра сказал, что, на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист.
2. Врач сказал, что он разделяет увлечение коллеги.
3. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Кто чем любит заниматься в свободное время и у кого какая профессия?
Задача 3.
Три друга — Иван, Дмитрий, Степан преподают различные предметы (химию, литературу, физику) в школах Москвы, Калининграда и Перми. Известно:
1) Иван работает не в Москве, а Дмитрий не в Калининграде;
2) москвич преподает не физику;
3) тот, кто работает в Калининграде, преподает химию;
4) Дмитрий преподает не литературу.
Какой предмет и в каком городе преподает каждый из товарищей?
Задача 4.
Четыре девочки Маша, Таня, София и Полина взяли в кафе сок. Каждая из них покупал только один сок, причем две из них купили сок яблочный, одна виноградный, и одна – грушевый. Известно, что у Маши и Тани разные вкусы. Разные соки взяли Маша с Софией, Полина с Софией, Полина с Машей и Таня с Софией. Кроме того известно, что Маша купила не грушевый сок. Определить, какой сок пила каждая из них.
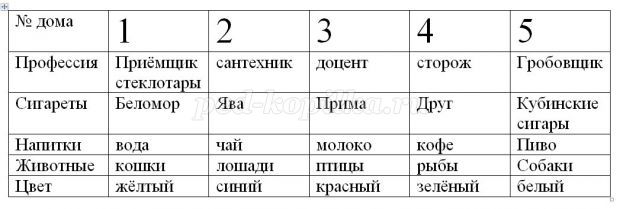
Задача 6. (Один из вариантов «Задачи Эйнштейна»)
Пять домов стоят вдоль дороги, один за другим.
1. Доцент живёт в красном доме.
2. Гробовщик держит собак.
3. Сантехник пьёт чай.
4. Зелёный дом слева от белого.
5. Хозяин зелёного дома пьёт кофе.
6. Любитель «Примы» держит птицу.
7. Хозяин жёлтого дома курит «Беломор канал».
8. В центральном доме любят молоко.
9. Приёмщик стеклотары живёт в первом доме.
10. Курящий «Яву» сосед хозяина кошек.
11. Хозяин лошадей – сосед курящего «Беломор».
12. Любитель пива курит «Кубинские» сигары.
13. Ночной сторож предпочитает сигареты «Друг».
14. Приёмщик стеклотары живёт рядом с синим домом.
15. Курящий «Яву» сосед пьющего воду.
Кто держит рыб? (номер дома, цвет профессия, напитки)
Решение:

Составить логическую задачу самостоятельно.
Удачи вам!

Задачи, составленные моими учениками.
Иванова Светлана, 7«Б» кл.
На дискотеку пошли 4 девочки: Маша, Оля, Рита. На медленный танец их приглашали Сергей, Рома, Саша, Паша. Кто с кем танцевал, если:
1) Оля не танцевала с Пашей;
2) Таня не танцевала с Пашей и Романом;
3) Рита танцевала с Ромой;
4) Оле понравился Сергей, но она не танцевала с ним.

Маякова Оксана, 9«А» кл.
Бизнесмены Боря Вова Гриша и Гена зарабатывают сумасшедшие деньги, их фамилии засекречены, но удалось их узнать, правда непонятно какая кому принадлежит. Их фамилии: Иванов, Енин, Сидоров, Петров. Так же наши шпионы выяснили:
1) Боря и Петров не имеют личные самолёты.
2) Гриша и Иванов вообще ничего личного не имеют, кроме счетов в швейцарском банке.
3) Гена теперь важнее Енина, хотя Енин и имеет личный самолёт.
4) Петров важнее Енина.
У кого какая фамилия?

Конева Ксения, 9«А» кл.
Четыре подружки: Даша, Маша, Ольга и Таня ходили в магазин покупать подарки. И все подарки разные. Блокнот, альбом, брелок, и книга. На вопрос кто какие подарки купил, они ответили так:
1) Даша и Оля не знали кто купил блокнот;
2) Оля сказала, что Даша и Маша вместе с ней посещали магазин, где продают брелки.
3) Даша не покупала альбом.
Кто какой подарок купил?

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 13.

Тема — Логические задачи и способы их решения

Перечень вопросов, рассматриваемых в теме: метод рассуждений, табличный метод, метод упрощения логических выражений.

Глоссарий по теме: для решения логических задач необходимо знать таблицы истинности логических операций и правила преобразования логических выражений (законы алгебры логики). Этот материал рассмотрен в предыдущих уроках №11,12.

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения

Исходными данными в логических задачах являются высказывания. Высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов сложно. Способов решения логических задач немало, но наибольшее распространение получили метод рассуждений, табличный метод и метод упрощения логических выражений. Познакомимся с ними поочередно.

Основная идея этого метода состоит в том, чтобы последовательно анализировать всю информацию, имеющуюся в задаче, и делать на этой основе выводы.

Пример 1. На одной улице стоят в ряд 4 дома, в каждом из которых живёт по одному человеку. Их зовут Василий, Семён, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что:

— столяр живёт правее охотника;

— врач живёт левее охотника;

— скрипач живёт с краю;

— скрипач живёт рядом с врачом;

— Семён не скрипач и не живёт рядом со скрипачом;

— Иван живёт рядом с охотником;

— Василий живёт правее врача;

— Василий живёт через дом от Ивана.

Определим, кто где живёт.

Изобразим дома прямоугольниками и пронумеруем их:

Известно, что скрипач живёт с краю (3). Следовательно, он может жить в доме 1 или в доме 4.

Скрипач живёт рядом с врачом (4), т. е. врач может жить правее (дом 2) или левее (дом 3) скрипача.

Но врач живёт левее охотника (2), следовательно, скрипач не может жить в доме 4, т. к. в противном случае получится, что врач, живущий рядом с ним, живёт правее охотника, а это противоречит условию (2). Таким образом, скрипач живёт в доме 1, а врач — рядом с ним, в доме 2.

Так как врач живёт левее охотника (2), а столяр — правее охотника (1), то охотнику достается дом 3, а столяру — дом 4.

Так как Семён не скрипач и не живёт рядом со скрипачом (5), то он может жить в доме 3 или в доме 4.

Так как Иван живёт рядом с охотником (6), то он может жить в доме 2 или 4.

Так как Василий живёт правее врача (7), то он может жить в доме 3 или 4.

По условию (8) Василий живет через дом от Ивана, значит, в доме 1 может жить только Геннадий, в доме 2 — Иван, в доме 4 — Василий, в доме 3 — Семён.

Как видите, далеко не самая сложна задача потребовала достаточно серьезных рассуждений. Этот метод, как правило, применяется для решения простых задач.

Задачи о рыцарях и лжецах — это такой класс логических задач, в которых фигурируют персонажи:

— рыцарь — человек, всегда говорящий правду;

— лжец — человек, всегда говорящий ложь;

— обычный человек — человек, который в одних ситуациях может говорить правду, а в других лгать.

Решение подобных задач сводится к перебору вариантов и исключению тех из них, которые противоречат условию.

Пример 2. Двое жителей острова А и В разговаривали между собой в саду. Проходивший мимо незнакомец спросил у А: «Вы рыцарь или лжец?». Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у В: «Что сказал А?».

«А сказал, что он лжец», — ответил В. Может ли незнакомец доверять ответу В? Мог ли А сказать, что он лжец?

Если А — рыцарь, то он скажет правду и сообщит, что он рыцарь.

Если А — лжец, то он скроет правду и сообщит, что он рыцарь.

Это значит, что В, утверждающий, что «А сказал, что он лжец» заведомо лжёт; он – лжец.

Определить, кем является А, в данной ситуации невозможно.

Для решения логических задач, связанных с рассмотрением нескольких конечных множеств, прибегают к помощи таблиц или графов. От того, насколько удачно выбрана их структура, во многом зависит успешность решения задачи.

Пример 3. В летнем лагере в одной палатке жили Алёша, Боря, Витя и Гриша. Все они разного возраста, учатся в разных классах (с 7-го по 10-й) и занимаются в разных кружках: математическом, авиамодельном, шахматном и фотокружке. Выяснилось, что

— фотограф старше Гриши;

— Алеша старше Вити, а шахматист старше Алёши;

— в воскресенье Алёша с фотографом играли в теннис, а Гриша в то же время проиграл авиамоделисту в городки.

Определим, кто в каком кружке занимается.

В этой задаче речь идёт о высказывательной форме (предикате) вида «Ученик х занимается в кружке у». Требуется определить такие значения х и у, чтобы высказывательная форма превратилась в истинное высказывание.

Рассмотрим условия (1)-(3) и сделаем выводы: Гриша — не фотограф (1); шахматист — не Алёша и не Витя (2); Алёша — не фотограф и не авиамоделист, Гриша — не фотограф и не авиамоделист (3). Отметим это в таблице:

Мы можем сделать вывод, что Алёша занимается математикой, а Гриша — шахматами:

Из того, что Гриша — шахматист и условий (1) и (2) можем расположить учеников по возрасту (в порядке возрастания): Витя — Алёша — Гриша — фотограф. Следовательно, Боря — фотограф.

Ответ: Витя (7 класс) занимается в авиамодельном кружке, Алёша (8 класс) — в математическом, Гриша (9 класс) — в шахматном, Боря (10 класс) — в фотокружке.

Использование таблиц истинности для решения логических задач

Аппарат алгебры логики позволяет применять к широкому классу логических задач универсальные методы, основанные на формализации условий задачи.

Одним из таких методов является построение таблицы истинности по условию задачи и её анализ. Для этого следует:

1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций.
3. Построить таблицу истинности для полученных логических выражений.
4. Выбрать решение – набор логических переменных (элементарных высказываний), при котором значения логических выражений соответствуют условиям задачи.
5. Убедиться, что полученное решение удовлетворяет условиям задачи.

Пример 4. Три подразделения А, В, С торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:

1. Если А получит максимальную прибыль, то максимальную прибыль получат В и С.
2. А и С получат или не получат максимальную прибыль одновременно.
3. Необходимым условием получения максимальной прибыли подразделением С является получение максимальной прибыли подразделением В.

По завершении года оказалось, что одно из трёх предположений ложно, а остальные два истинны.

Выясним, какие из названных подразделений получили максимальную прибыль.

Рассмотрим элементарные высказывания:

А — «А получит максимальную прибыль»;

В — «В получит максимальную прибыль»;

С — «С получит максимальную прибыль».

Запишем на языке алгебры логики прогнозы, высказанные экономистами:

Вспомним, что из трёх прогнозов F₁, F₂, F₃ один оказался ложным, а два других — истинным. Эта ситуация соответствует четвёртой строке таблицы.

Ответ: максимальную прибыль получили подразделения В и С.

Метод упрощения логических выражений

Следующий формальный способ решения логических задач состоит в том, чтобы:

1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций.
3. Составить единое логическое выражение, учитывающее все требования задачи.
4. Используя законы алгебры логики, упростить полученное выражение и вычислить его значение.
5. Выбрать решение – набор логических переменных (элементарных высказываний), при котором построенное логическое выражение является истинным.
6. Убедиться, что полученное решение удовлетворяет условиям задачи.

Пример 5. На вопрос, кто из трёх учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?

Обозначим через А, В, С простые высказывания:

А — «Первый ученик изучал логику»;

В — «Второй ученик изучал логику»;

С — «Третий ученик изучал логику».

Из условия задачи следует истинность высказывания: .

Упростим получившееся высказывание:

Получившееся высказывание будет истинным только в случае, если С — истина, а А и В — ложь.

Источник