Средства представления алгоритмов
Процесс составления алгоритмов называют алгоритмизацией. Алгоритм можно представить различными способами: с помощью графического или текстового описания, в виде таблицы значений.
Графический способ представления алгоритмов имеет ряд преимуществ благодаря визуальности процесса решения задачи. Алгоритмы, представленные графическими средствами, получили название визуальные алгоритмы или блок – схемы .
Текстовое описание алгоритма является достаточно компактным и может быть реализовано на абстрактном или реальном языке программирования в виде программы для ЭВМ. Таблицы значений представляют алгоритм неявно, как некоторое преобразование конкретных исходных данных в выходные.
Табличный способ описания алгоритмов. Применяют для проверки правильности функционирования алгоритма на конкретных тестовых наборах входных данных, которые вместе с результатами выполнения алгоритма фиксируются в «таблицах трассировки».
Все три способа представления алгоритмов являются взаимодополняющими. На этапе проектирования наилучшим является графическое представление, на этапе проверки алгоритма — табличное описание, на этапе применения — текстовая запись в виде программы.
Визуальное представление алгоритмов
При проектировании визуальных алгоритмов используют специальные графические элементы, называемые графическими блоками, которые представ-лены в таблице. Существует Государственный стандарт (ГОСТ 19.002-80 и ГОСТ 19.003-80), определяющий правила выполнения схем и обозначения для отдельных операций.
Правила проектирования визуальных алгоритмов:
• В начале алгоритма должны быть блоки ввода значений входных данных.
• После ввода значений входных данных следуют блоки обработки и блоки условия.
• В конце алгоритма должны располагаться блоки вывода значений выходных данных.
• В алгоритме должен быть только один блок начала и один блок окончания.
• Связи между блоками указываются направленными или ненаправленными линиями.
• Данные, вычислительные формулы, логические выражения располагают внутри соответствующих блоков.
• Блоки могут сопровождаться комментариями в виде выносок.
Графическое представление алгоритмов имеет практическое значение не только для программистов. Те же информационные схемы (инфографика) используются журналистами для визуализации данных. Структурные схемы последовательности монтажа полезны для сборщиков мебели, например. Та же визуализация алгоритма трассировки (алгоритм Ли) может быть полезна для конструирования печатных плат, особенно когда требуется срочное изготовление таких плат по требованиям заказчика.
Источник
Средства описания алгоритмов
Алгоритм моделирует решение задачи в виде точно определенной последовательности действий для некоторого исполнителя по преобразованию исходных данных в результирующие.
Для его описания используется алгоритмический язык – набор символов и правил образования и истолкования конструкций из этих символов для записи алгоритмов.
Основными изобразительными средствами алгоритмов являются следующие способы их записи:
Словесный способ предполагает словесное (без формул и таблиц) описание алгоритма. Этим способом можно описывать алгоритмы с любой степенью детализации.
При этом способе отсутствует наглядность вычислительного процесса, т.к. нет достаточной формализации.
На рисунке 3.1 приведен пример словесной записи алгоритма. Пусть задан массив чисел. Требуется проверить, все ли числа принадлежат заданному интервалу. Интервал задается границами А и В.
Рисунок 3.1. Пример словесной записи алгоритма
Никаких правил составления словесного описания не существует. Запись алгоритма осуществляется в произвольной форме на естественном, например, русском языке. Этот способ описания не имеет широкого распространения, так как допускает неоднозначность толкования при описании некоторых действий.
Формульно-словесный способ более компактный. Он предполагает задание инструкций с использованием математических символов и выражений в сочетании со словесными пояснениями.
Например, требуется написать алгоритм вычисления площади треугольника по трем сторонам (рисунок 3.2).
Рисунок 3.2. Пример формульно-словесной записи алгоритма
При использовании этого способа может быть достигнута любая степень детализации, более наглядно, но не строго формально.
Графический способ получил наибольшее распространение. В этом способе алгоритм представляется в виде схемы, состоящей из элементов символов, отражающих отдельные операции технологического процесса обработки данных и отдельные вычислительные операции.
Каждый этап процесса переработки данных представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера выполняемых операций (таблица 3.1).
Таблица 3.1 Основные конструкции, применяемые для построения блок-схем
| Оператор блок-схемы | Описание |
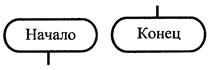 | Блок, характеризующий начало/конец алгоритма |
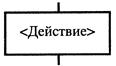 | Блок, предназначенный для описания отдельных действий (процесс) |
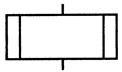 | Блок, предназначенный для обращения к вспомогательным алгоритмам (предопределенный процесс) |
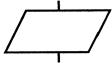 | Блок ввода/вывода |
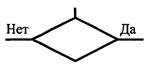 | Блок «решение» (проверка условия или условный блок) |
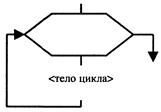 | Блок, описывающий цикл |
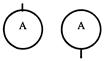 | Соединительные блоки |
Алгоритмы, представленные графическими средствами, получили название визуальные алгоритмы.
Общими правилами при проектировании визуальных алгоритмов являются следующие:
— В начале алгоритма должны быть блоки ввода значений входных данных.
— После ввода значений входных данных могут следовать блоки обработки и блоки условия.
— В конце алгоритма должны располагаться блоки вывода значений выходных данных.
— В алгоритме должен быть только один блок начала и один блок окончания.
— Связи между блоками указываются направленными или ненаправленными линиями.
Псевдокод позволяет формально изображать логику программы, не заботясь при этом о синтаксических особенностях конкретного языка программирования. Обычно представляет собой смесь операторов языка программирования и естественного языка. Является средством представления логики программы, которое можно применять вместо блок-схемы (рисунок 3.3).
Рисунок 3.3. Запись алгоритма в виде псевдокода
Строгих синтаксических правил для записи псевдокода не существует, Это облегчает запись алгоритма при проектировании и позволяет описать алгоритм, используя любой набор команд. Однако в псевдокоде обычно используются некоторые конструкции, присущие формальным языкам, что облегчает переход от псевдокода к записи алгоритма на языке программирования. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором используемых слон и конструкций.
Таблицы значений представляют алгоритм неявно, как некоторое преобразование конкретных исходных данных в выходные. Табличный способ описания алгоритмов может быть с успехом применен для проверки правильности функционирования разработанного алгоритма на конкретных тестовых наборах входных данных, которые вместе с результатами выполнения алгоритма фиксируются в «таблицах трассировки». Данный способ носит, в основном, вспомогательный характер.
Операторный способ предполагает представление алгоритма в виде последовательности операторов. Возможность рассматривать дискретный алгоритм, являющийся совокупностью элементарных предписаний (инструкций), как совокупность элементарных операторов, следует из того, что каждое элементарное предписание можно считать оператором. Для описания элементарных операторов вводятся обозначения, определяемые языком программирования.
Таким образом, все способы представления алгоритмов можно считать взаимодополняющими друг друга. Например, на этапе проектирования алгоритмов наилучшим способом является графическое представление, на этапе проверки алгоритма — табличное описание, на этапе применения — запись в виде программы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способы записи алгоритмов
На практике применяются алгоритмы следующих типов:
Линейные алгоритмы
Это алгоритмы, у которых последовательность операций при исполнении совпадает с порядком их следования в записи алгоритма и не зависит от конкретных значений исходных данных. С помощью таких алгоритмов реализуются задачи типа:
Y = А*Х+В
разветвляющиеся, ветвящиеся алгоритмы. Такие алгоритмы
используются для решения задач, в которых заложена операция выбора одной из формул, в зависимости от заданного
значения переменной. Такие алгоритмы используются при
решение задач, типа:
Y=Ln x, при x>=1
Y=1-x, при x n
Для записи алгоритмов обычно используют табличный, словесный и схематичный способы записи.
Табличный способ записи алгоритмов
Табличный способ записи алгоритмов применяется, когда требуется вычислить не одно, а несколько значений одного и того же выражения для различных значений входных величин.
Например, требуется вычислить площадь поверхности цилиндрического тела по формуле:
S=3.14*(D*H+D 2 /2)
где D — диаметр, Н — высота.
Табличный алгоритм вычисления площади поверхности тела по указанной формуле представлен в таблице:
| D | H | 3.14*D | 3.14*D 2 | 3.14*D 2 /2 | 3.14*D*H | S |
|---|---|---|---|---|---|---|
| 6 | 4 | 18,84 | 113,04 | 56,52 | 75,36 | 131,88 |
| 5 | 10 | 15,7 | 78,5 | 39,25 | 157 | 196,25 |
| 10 | 12 | 31,4 | 314 | 157 | 376,8 | 533,8 |
Словесный способ записи алгоритмов
Одна из самых распространенных форм представлении алгоритмов — словесная форма. Особенностью словесной представления алгоритма является то, что таким cnocoбом могут быть описаны любые алгоритмы, в том числе и вычислительные.
Опишем последовательность действий для вычислений по формуле:
Y=(6*x+25)/2.
1) Прочитаем заданное значение X;
2) Умножим X на 6;
3) К результату второго действия прибавим 25;
4) Результат третьего действия разделим на 2;
5) Запишем значение результата Y;
В результате получили словесную запись линейного вычислительного алгоритма.
В приведенном вычислительном алгоритме X является входной величиной (исходным значением, аргументом), а Y выходной величиной (результатом).
В словесной записи алгоритма, если при исполнении текущего предписания не указывается явно номер очередного предписания, происходит автоматический переход к предписанию, следующему за данным в порядке возрастания номеров.
После исполнения предписания с наибольшим номером, процесс выполнения алгоритма заканчивается.
Для удобства рекомендуется заканчивать запись словес о алгоритма специальным предписанием «конец».
При записи вычислительных алгоритмов удобно использовать специальный знак присваивания :=. Этот знак используется для записи специальной операции операции присваивания. Смысл операции присваивания состоит в том, что некоторой переменной, имя которой указывается слева, присваивается значение некоторого выражения, указанного справа.
Например, предписание, вида Y:=X читается так: «переменной Y присвоить значение X». Если X — является формулой, тогда нужно выполнить все действия, предусмотренные формулой и полученный результат (число) присвоить переменной Y.
Операция присваивания может быть обозначена и обычным знаком равенства или стрелками: A:=D*B, A=D*B, A->D*B.
Используя знак операции присваивания и вспомогательные переменные, в которых будут запоминаться промежуточные значения, можно сделать запись приведенного выше словесного алгоритма значительно компактнее:
После составления словесного алгоритма необходимо провести контроль правильности составления алгоритма. Проверка алгоритма в таблице состоит в том, что выбираются конкретные исходные данные и составленный алгоритм выполняется в строгом соответствии с записанными предписаниями.
Таблица контроля правильности алгоритма вычисления Y=(6*X+25)/2
| Шаги алгоритма | Аргумент X | Промежуточная величина А | Промежуточная величина B | Результат Y | Пояснения |
| 1 | 2 | чтение X | |||
| 2 | 12 | ||||
| 3 | 37 | ||||
| 4 | 18.5 | ||||
| 5 | запись 18.5 | ||||
| 6 | остановка |
Важное свойство операции присваивания состоит в том, что одна и та же переменная может находиться и слева и справа от знака присваивания, т.е. можно записать
А := А+В.
Такая запись означает, что к значению переменной А, которое она имела до начала выполнения операции присваивания, прибавляется значение переменной В и полученное в результате значение присваивается переменной А (становится новым значением переменной А). Прежнее значение переменной А при этом пропадает.
Используя это свойство операции присваивания, можно отказаться от использования избыточных промежуточных переменных.
Тогда запись алгоритма вычисления Y будет иметь следующий вид:
В приведенном примере можно не использовать ни одной вспомогательной переменной, т.к. для хранения промежуточных результатов достаточно использовать одну переменную Y.
Таблица проверки правильности алгоритма наглядно показывает механизм проведенных присваиваний.
Таблица контроля правильности алгоритма вычисления Y=(6*x+25)/2 без избыточных вспомогательных переменных
Источник







