Что такое способы построения различных

Черчение

Способы построения видов на чертеже

Построение видов начинается с мысленного выбора положе­ния детали перед плоскостями проекций. Затем выбирают коли­чество видов, необходимых и достаточных для выявления формы детали, а также способ их построения.

Выбор положения детали в системе плоскостей проекций за­висит от ее рабочего положения, способа изготовления на произ­водстве, формы. Например, если деталь изготавливается на то­карном станке, то на чертеже ее ось вращения должна распола­гаться горизонтально.

Виды чертежа могут быть выполнены различными способами. Рассмотрим некоторые из них.

Построение видов на основе последовательного вычерчива­ния геометрических тел, составляющих форму предмета. Для того чтобы выполнить чертеж этим способом, необходимо мысленно разделить деталь на составляющие ее простые геометри­ческие тела, выяснив, как они расположены относительно друг друга. Затем нужно выбрать главный вид детали и число изо­бражений, позволяющие понять ее форму и последовательно изобразить одно геометрическое тело за другим до полного ото­бражения формы объекта. Необходимо соблюдать размеры фор­мы и правильно ориентировать ее элементы относительно друг друга (табл. 8).

Построение видов на основе поэлементного вычерчивания геометрических тел, составляющих форму предмета, осуществля­ется с помощью приемов удаления и приращения.

При вычерчивании геометрического тела с использованием приема удаления на чертеже последовательно изменяется форма заготовки с помощью удаления объемов схожих с приемами ее обработки точением, сверлением, фрезерованием и т. п.

При вычерчивании геометрического тела с использованием приема приращения объемы элементов изделия как бы допол­няют друг друга, приращиваются.

8. Поэлементное вычерчивание геометрических тел, составляющих форму предмета

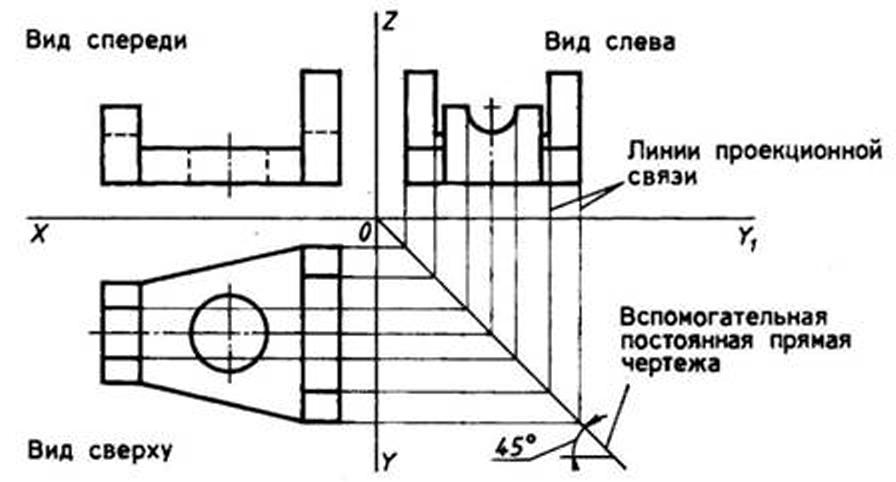
Построение видов с помощью постоянной прямой чертежа (способ внешнего координирования). Постоянной прямой чер­тежа называют линию, которую проводят из центра координат (точки О) вниз направо под углом 45° (рис. 86).

Предмет мысленно размещают в системе плоскостей проек­ций. Оси плоскостей проекций принимают за координатные оси. Проекционную связь между видом сверху и видом слева осуще­ствляют с помощью линий проекционной связи, которые прово­дят до пересечения с постоянной прямой чертежа и строят под углом 90° друг к другу.

Постоянную прямую чертежа, как правило, используют в тех случаях, когда по двум заданным видам необходимо построить третий вид детали (см. рис. 86). Перечертив два вида детали, строят постоянную прямую чертежа и проводят линии проекци­онной связи параллельно оси ОХ до пересечения с постоянной прямой чертежа, а затем — параллельно оси OZ.

Рассмотренный способ построения называют способом внеш­него координирования, поскольку предмет фиксируется в про­странстве относительно осей плоскостей проекций, которые рас­полагаются вне изображаемого объекта.

(Если на чертеже не показаны оси проекций и необходи­мо выполнить третий вид детали, то можно построить постоян­ную прямую чертежа в любом месте с правой стороны от вида сверху.)

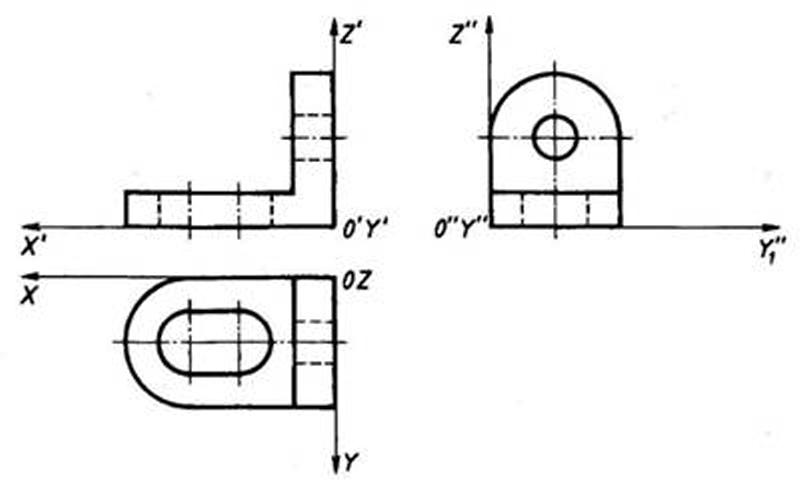
Построение видов с помощью внутреннего координирования объекта. Внутреннее координирование заключается в мысленном введении дополнительных осей координат, привязанных к проецируемому предмету.

Рис. 86. Построение третьей проекции по двум заданным с помощью постоянной прямой чертежа

Рис. 87. Построение видов способом внутреннего координирования объекта

Источник

Какими бывают способы построения:

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова исподники (существительное):

Ассоциации к слову «способ&raquo

Ассоциации к слову «построение&raquo

Синонимы к слову «способ&raquo

Синонимы к слову «построение&raquo

Предложения со словосочетанием «способы построения&raquo

• Зодчие, работавшие в то время, стремились к тому, чтобы открыть новые способы построения и изображения действительности.

Значение слова «способ&raquo

СПО́СОБ , -а, м. Образ действий, прием осуществления чего-л. Способ изготовления стекла. Решение задачи различными способами. (Малый академический словарь, МАС)

Значение слова «построение&raquo

ПОСТРОЕ́НИЕ , -я, ср. 1. Действие по знач. глаг. построить и построиться. Построение коммунистического общества. Построение геометрических фигур по заданным элементам. (Малый академический словарь, МАС)

Афоризмы русских писателей со словом «способ&raquo

• Стихи — совершеннейший из способов пользоваться человеческим словом, и разменивать его на мелочи, пользоваться им для пустяков — грешно и стыдно…

Отправить комментарий

Дополнительно

Значение слова «способ&raquo

СПО́СОБ , -а, м. Образ действий, прием осуществления чего-л. Способ изготовления стекла. Решение задачи различными способами.

Значение слова «построение&raquo

ПОСТРОЕ́НИЕ , -я, ср. 1. Действие по знач. глаг. построить и построиться. Построение коммунистического общества. Построение геометрических фигур по заданным элементам.

Предложения со словосочетанием «способы построения&raquo

Зодчие, работавшие в то время, стремились к тому, чтобы открыть новые способы построения и изображения действительности.

При использовании второго способа построения следует ввести координаты начальной и конечной точек условного отрезка, с которым будет совмещена одна из его сторон.

Риторикав настоящее время – это филологическая наука, изучающая способы построения художественно выразительной, направленной и определённым образом воздействующей речи.

Источник

LiveInternetLiveInternet

—Метки

—Ссылки

—Фотоальбом

—Рубрики

• уроки рисования. (58)
• анимэ (6)
• цветы (5)
• свет и тень (1)
• художники (27)
• рисунки (19)
• черчение (15)
• всякие разности (13)
• одежда для собак (1)
• фоны (5)
• бумажная пластика (4)
• каллиграфия (3)
• музыка (2)
• архитектура (1)
• дополнительные задания для учеников (1)
• мифы (1)
• сюжетный портрет (0)

—Приложения

• Я — фотографПлагин для публикации фотографий в дневнике пользователя. Минимальные системные требования: Internet Explorer 6, Fire Fox 1.5, Opera 9.5, Safari 3.1.1 со включенным JavaScript. Возможно это будет рабо
• ОткрыткиПерерожденный каталог открыток на все случаи жизни

—Цитатник

Мастер декупажа — Елена Олейникова. «. в синих тонах» Елена Олейникова

3D Photo Effects — экшен для фотошоп ПАМЯТКА НАЧИНАЮЩИМ ФОТОШОППЕРАМ .

Продолжение клада.Орнамент всех времен и стилей.Третья часть. первая и вторая часть здесь -htt.

Текстильные фоны для творчества. Часть 1. .

Девочка. Урок рисования. Акварель. Рисуем девочку акварельными кра.

—Поиск по дневнику

—Подписка по e-mail

—Друзья

—Постоянные читатели

—Сообщества

—Статистика

Способы построения видов на чертеже

Понедельник, 16 Апреля 2012 г. 17:02 + в цитатник

Построение видов начинается с мысленного выбора положения детали перед плоскостями проекций. Затем выбирают количество видов, необходимых и достаточных для выявления формы детали, а также способ их построения.

Выбор положения детали в системе плоскостей проекций зависит от ее рабочего положения, способа изготовления на производстве, формы. Например, если деталь изготавливается на токарном станке, то на чертеже ее ось вращения должна располагаться горизонтально.

Виды чертежа могут быть выполнены различными способами. Рассмотрим некоторые из них.

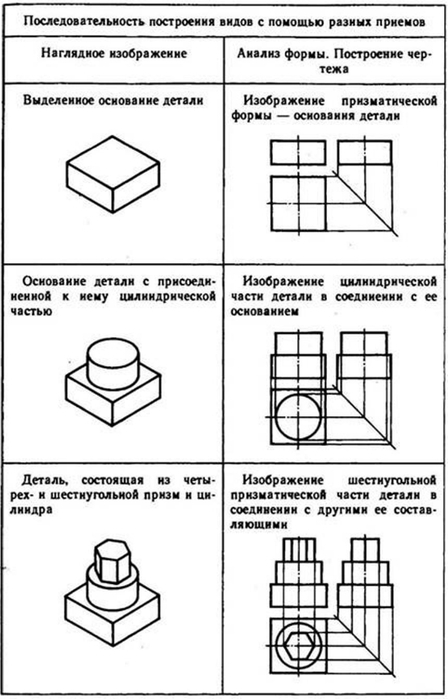
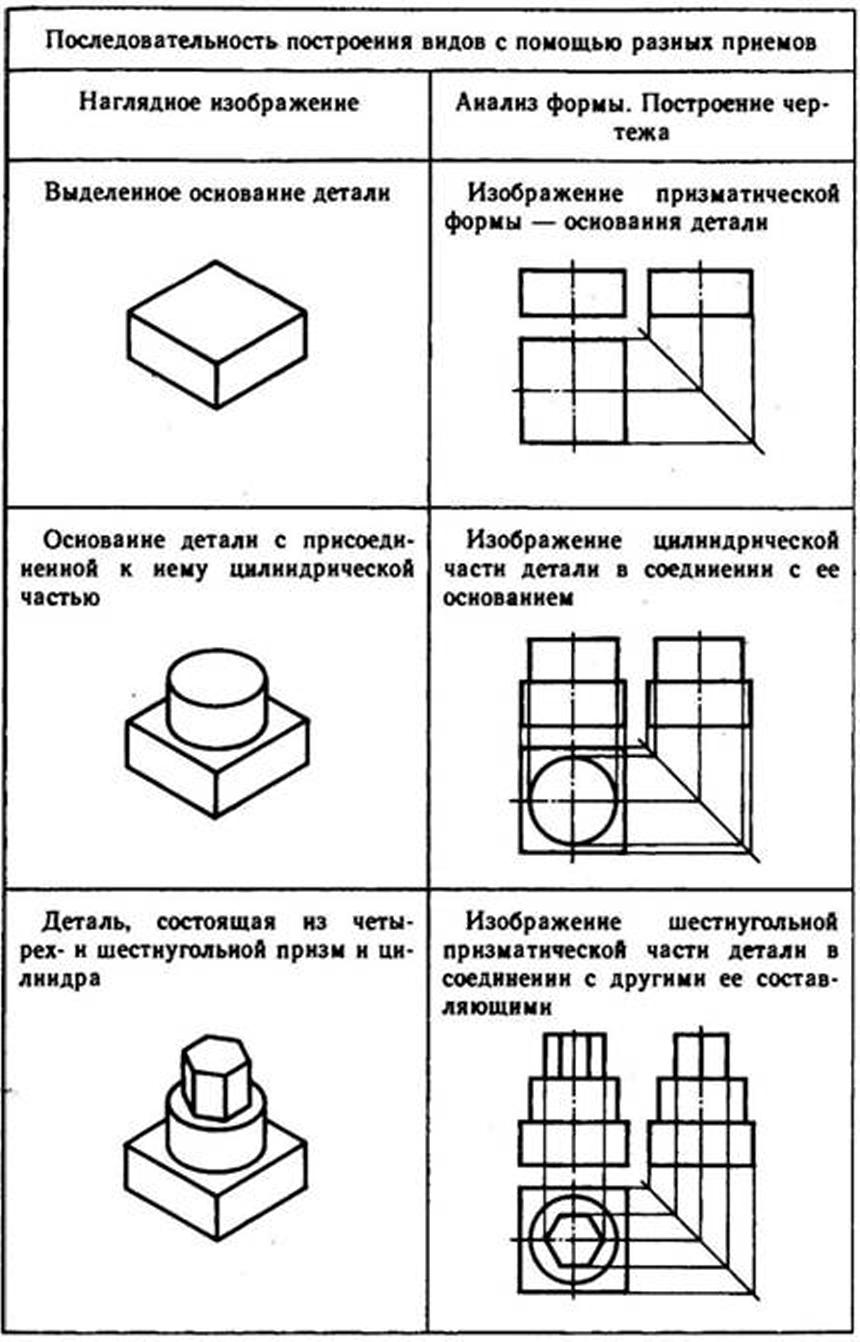
Построение видов на основе последовательного вычерчивания геометрических тел, составляющих форму предмета. Для того чтобы выполнить чертеж этим способом, необходимо мысленно разделить деталь на составляющие ее простые геометрические тела, выяснив, как они расположены относительно друг друга. Затем нужно выбрать главный вид детали и число изображений, позволяющие понять ее форму и последовательно изобразить одно геометрическое тело за другим до полного отображения формы объекта. Необходимо соблюдать размеры формы и правильно ориентировать ее элементы относительно друг друга (табл. 8).

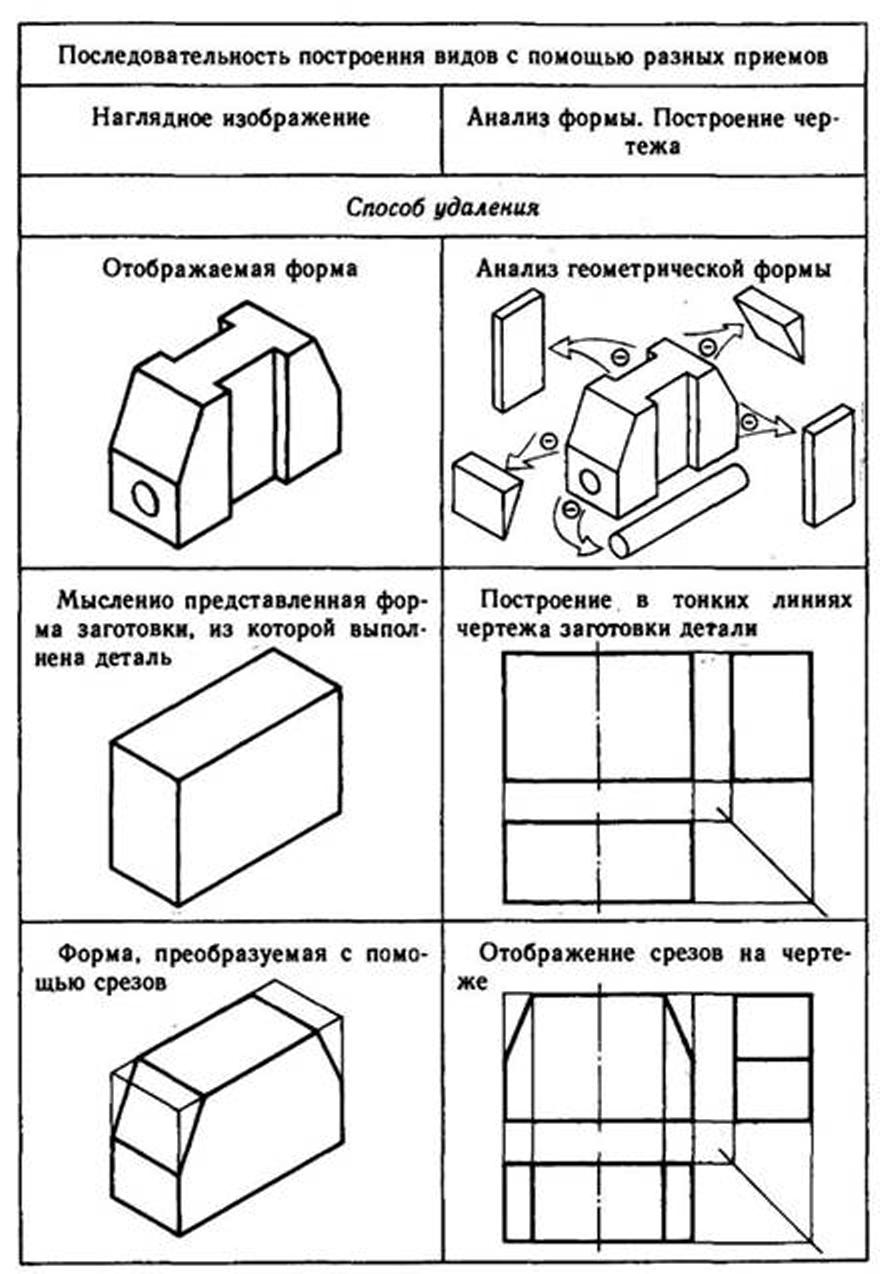
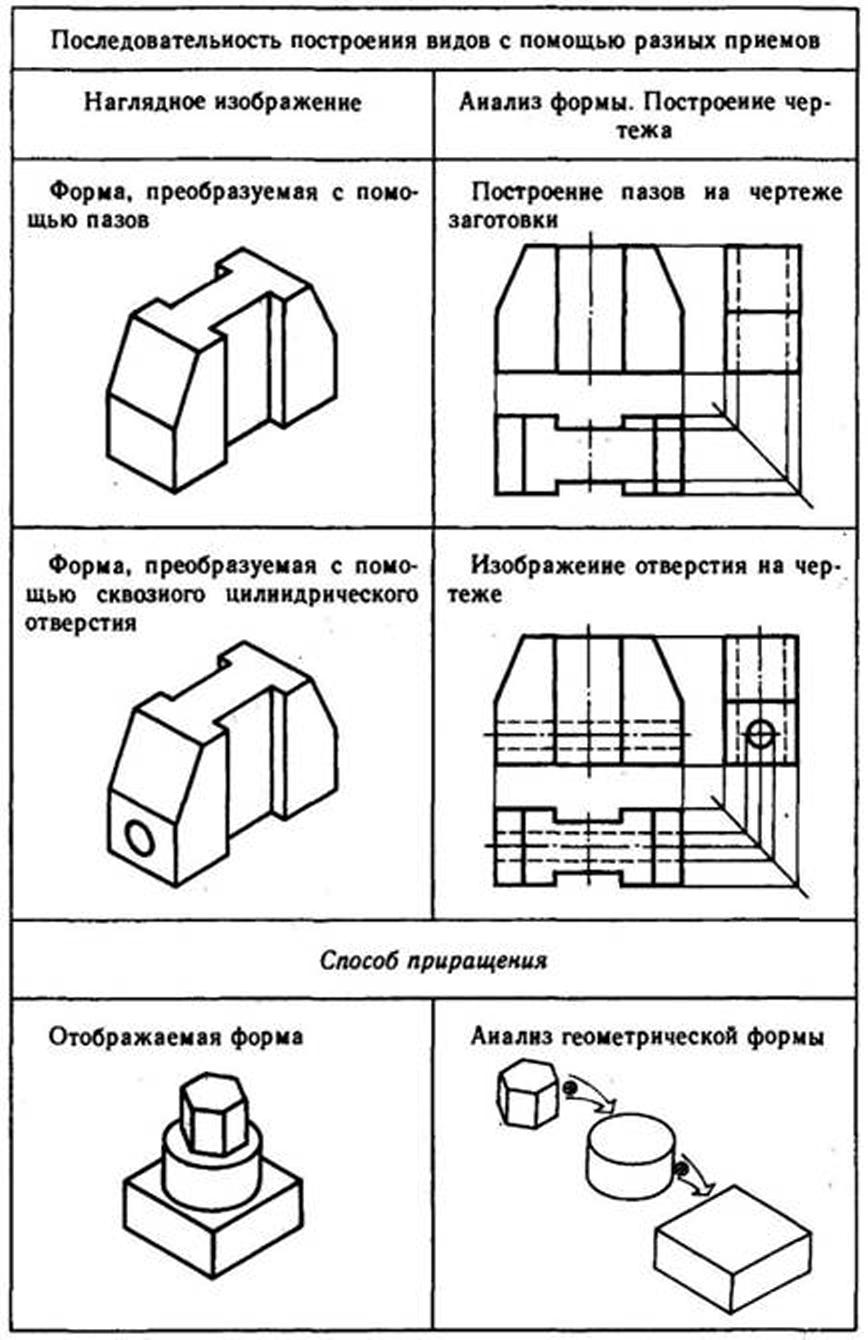
Построение видов на основе поэлементного вычерчивания геометрических тел, составляющих форму предмета, осуществляется с помощью приемов удаления и приращения.

При вычерчивании геометрического тела с использованием приема удаления на чертеже последовательно изменяется форма заготовки с помощью удаления объемов схожих с приемами ее обработки точением, сверлением, фрезерованием и т. п.

При вычерчивании геометрического тела с использованием приема приращения объемы элементов изделия как бы дополняют друг друга, приращиваются.

3.

Построение видов с помощью постоянной прямой чертежа (способ внешнего координирования). Постоянной прямой чер­тежа называют линию, которую проводят из центра координат (точки О) вниз направо под углом 45° (рис. 86).

Предмет мысленно размещают в системе плоскостей проекций. Оси плоскостей проекций принимают за координатные оси. Проекционную связь между видом сверху и видом слева осуществляют с помощью линий проекционной связи, которые проводят до пересечения с постоянной прямой чертежа и строят под углом 90° друг к другу.

Постоянную прямую чертежа, как правило, используют в тех случаях, когда по двум заданным видам необходимо построить третий вид детали (см. рис. 86). Перечертив два вида детали, строят постоянную прямую чертежа и проводят линии проекционной связи параллельно оси ОХ до пересечения с постоянной прямой чертежа, а затем — параллельно оси OZ.

Рассмотренный способ построения называют способом внешнего координирования, поскольку предмет фиксируется в пространстве относительно осей плоскостей проекций, которые располагаются вне изображаемого объекта.

(Если на чертеже не показаны оси проекций и необходимо выполнить третий вид детали, то можно построить постоян­ную прямую чертежа в любом месте с правой стороны от вида сверху.)

Построение видов с помощью внутреннего координирования объекта. Внутреннее координирование заключается в мысленном введении дополнительных осей координат, привязанных к проецируемому предмету.

Источник

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

1. 
2. 
3. 

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
0	-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

x	y
0	2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

x	y
0	0
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Источник