Что такое способ триангуляции

Триангул я ция (от лат. triangulum — треугольник) — один из методов создания опорной геодезической сети.

Состоит в построении рядов или сетей примыкающих друг к другу треугольников и в определении положения их вершин в избранной системе координат. В каждом треугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путём последовательного решения предыдущих треугольников, начиная от того из них, в котором одна из его сторон получена из измерений. Если сторона треугольника получена из непосредственных измерений, то она называется базисной стороной триангуляции. В рядах или сетях триагуляции для контроля и повышения их точности измеряют большее число базисов или базисных сторон, чем это минимально необходимо.

Принято считать, что метод триангуляции изобрёл и впервые применил В. Снеллиус в 1615–17 гг. при прокладке ряда треугольников в Нидерландах для градусных измерений. Работы по применению метода триангуляции для топографических съёмок в дореволюционной России начались на рубеже 18–19 вв. К началу 20 в. метод триангуляции получил повсеместное распространение.

Триангуляция имеет большое научное и практическое значение. Она служит для: определения фигуры и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.

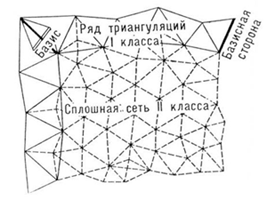
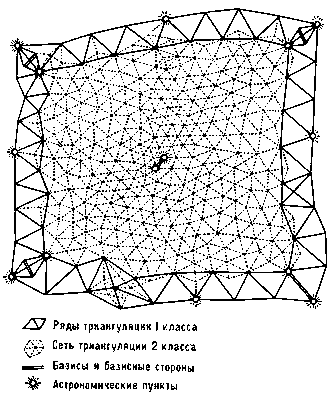
При построении триангуляции в государственной геодезической сети (ГГС) исходят из принципа перехода от общего к частному, от крупных треугольников к более мелким. В связи с этим триангуляция подразделяется на классы, отличающиеся точностью измерений и последовательностью их построения. В малых по территории странах триангуляция высшего класса строят в виде сплошных сетей треугольников. В государствах с большой территорией (Россия, Китай, Индия, США, Канада и др.) триангуляцию строят по некоторой схеме и программе.

Государственная триангуляция РФ делится на 4 класса (рис.).

Государственная триангуляция 1-го класса строится в виде рядов треугольников со сторонами 20–25 км, расположенных примерно вдоль меридианов и параллелей и образующих полигоны с периметром 800–1000 км. Углы треугольников в этих рядах измеряют высокоточными теодолитами, с погрешностью не более ± 0,7″. В местах пересечения рядов триангуляции 1-го класса измеряют базисы при помощи мерных проволок, причём погрешность измерения базиса не превышает 1 : 1000000 доли его длины, а выходные стороны базисных сетей определяются с погрешностью около 1 : 300 000. После изобретения высокоточных электрооптических дальномеров стали измерять непосредственно базисные стороны с погрешностью не более 1 : 400 000.

Пространства внутри полигонов триангуляции 1-го класса покрывают сплошными сетями треугольников 2-го класса со сторонами около 10–20 км, причём углы в них измеряют с той же точностью, как и в 1-ом классе. В сплошной сети триангуляции 2-го класса внутри полигона 1-го класса измеряется также базисная сторона с указанной выше точностью. На концах каждой базисной стороны 1-го и 2-го классов выполняют астрономические определения широты и долготы с погрешностью не более ± 0,4«, а также азимута с погрешностью около ± 0,5«. Кроме того, астрономические определения широты и долготы выполняют и на промежуточных пунктах рядов триангуляции 1-го класса через каждые примерно 100 км, а по некоторым особо выделенным рядам и значительно чаще.

На основе рядов и сетей триангуляции 1-го и 2-го классов определяют пункты триангуляции 3-го и 4-го классов, причём их густота зависит от масштаба топографической съёмки. Например, при масштабе съёмки 1 : 5000 один пункт триангуляции должен приходиться на каждые 20–30 км 2 . В сетях триангуляции 3-го и 4-го классов погрешности измерения углов не превышают соответственно 1,5« и 2,0«.

В практике допускается вместо триангуляции применять метод полигонометрии. При этом ставится условие, чтобы при построении опорной геодезической сети тем и др. методом достигалась одинаковая точность определения положения пунктов земной поверхности.

Вершины треугольников триангуляции. обозначаются на местности деревянными или металлическими вышками высотой от 6 до 55 м в зависимости от условий местности (см. Сигнал геодезический). Пункты триангуляции в целях долговременной их сохранности на местности закрепляются закладкой в грунт особых устройств в виде металлических труб или бетонных монолитов с вделанными в них металлическими марками (см. Центр геодезический), фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.

Координаты пунктов триангуляции определяют из математической обработки рядов или сетей. Построение триангуляции и её математическая обработка приводят к созданию на всей территории страны единой системы координат, позволяющей ставить топографо-геодезические работы в разных частях страны одновременно и независимо друг от друга. При этом обеспечивается соединение этих работ в одно целое и создание единой общегосударственной топографической карты страны в установленном масштабе.

Источник

Триангуляция

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Полезное

Смотреть что такое «Триангуляция» в других словарях:

ТРИАНГУЛЯЦИЯ — (позд. лат., от лат. triangalus треугольник.). Тригонометрическое действие, при посредстве которого снимают план с известной местности, разделивши ее на треугольники, которые вычисляются при помощи тригонометрических формул. Словарь иностранных… … Словарь иностранных слов русского языка

Триангуляция — (геодезия) один из методов создания сети опорных геодезических пунктов и сама сеть. В математике Триангуляция (топология) разбиение топологического пространства на симплексы. Триангуляция Делоне … Википедия

Триангуляция — (от лат. triangulum треугольник * a. triangulation, survey by triangulation; н. Triangulation; ф. triangulation; и. tciangulacion) один из методов создания сети опорных геодезич. пунктов, заключающийся в построении рядов или сетей из… … Геологическая энциклопедия

ТРИАНГУЛЯЦИЯ — ТРИАНГУЛЯЦИЯ, см. тригонометрия. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

триангуляция — Метод построения геодезической сети в виде треугольников, в которых измерены их углы и некоторые из сторон [ГОСТ 22268 76] триангуляция Метод определения планового положения геодезических пунктов путём построения на местности системы смежных или… … Справочник технического переводчика

ТРИАНГУЛЯЦИЯ — (от лат. triangulum треугольник) метод определения положения геодезических пунктов построением на местности систем смежно расположенных треугольников, в которых измеряют длину одной стороны (по базису) и углы, а длины других сторон получают… … Большой Энциклопедический словарь

ТРИАНГУЛЯЦИЯ — (тригонометрическая съемка), в навигации и топографической съемке метод определения расстояния. Площадь съемки делится на треугольники. Затем ТЕОДОЛИТОМ измеряют основание треугольника и прилежащие углы. Расстояния от концов основания до… … Научно-технический энциклопедический словарь

ТРИАНГУЛЯЦИЯ — ТРИАНГУЛЯЦИЯ, триангуляции, мн. нет, жен. (от лат. triangulus треугольник). 1. Вычисление углов и протяжений методами тригонометрии (мат.). 2. Определение взаимного расположения точек на поверхности при помощи построения сети треугольников… … Толковый словарь Ушакова

ТРИАНГУЛЯЦИЯ — (Triangulation) наиболее точный прием определения взаимного расположения точек на земной поверхности. При Т. выбираются на открытых и возвышенных местах опорные пункты и закрепляются постройкой специальных знаков. Стороны между знаками образуют… … Морской словарь

ТРИАНГУЛЯЦИЯ — горизонтальная съемка расположения вершин сети треугольников путем измерения длины одной стороны базиса и измерения всех углов. Т. применяется для точной съемки больших участков земной поверхности или для определения длины дуги меридиана или… … Технический железнодорожный словарь

триангуляция — сущ., кол во синонимов: 2 • аэротриангуляция (1) • стереотриангуляция (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Источник

Триангуляция (в геодезии)

Принято считать, что метод Т. изобрёл и впервые применил В. Снеллиус в 1615‒17 при прокладке ряда треугольников в Нидерландах для градусных измерений . Работы по применению метода Т. для топографических съёмок в дореволюционной России начались на рубеже 18‒19 вв. К началу 20 в. метод Т. получил повсеместное распространение.

Т. имеет большое научное и практическое значение. Она служит для: определения фигуры и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.

При построении Т. исходят из принципа перехода от общего к частному, от крупных треугольников к более мелким. В связи с этим Т. подразделяется на классы, отличающиеся точностью измерений и последовательностью их построения. В малых по территории странах Т. высшего класса строят в виде сплошных сетей треугольников. В государствах с большой территорией (СССР, Канада, КНР, США и др.) Т. строят по некоторой схеме и программе. Наиболее стройная схема и программа построения Т. применяется в СССР.

Государственная Т. в СССР делится на 4 класса ( рис. ). Государственная Т. СССР 1-го класса строится в виде рядов треугольников со сторонами 20‒25 км , расположенных примерно вдоль меридианов и параллелей и образующих полигоны с периметром 800‒1000 км . Углы треугольников в этих рядах измеряют высокоточными теодолитами , с погрешностью не более ╠ 0,7 » . В местах пересечения рядов Т. 1-го класса измеряют базисы при помощи мерных проволок (см. Базисный прибор ), причём погрешность измерения базиса не превышает 1 : 1000000 доли его длины, а выходные стороны базисных сетей определяются с погрешностью около 1 : 300 000. После изобретения высокоточных электрооптических дальномеров стали измерять непосредственно базисные стороны с погрешностью не более 1 : 400 000. Пространства внутри полигонов Т. 1-го класса покрывают сплошными сетями треугольников 2-го класса со сторонами около 10‒20 км , причём углы в них измеряют с той же точностью, как и в Т. 1-го класса. В сплошной сети Т. 2-го класса внутри полигона 1-го класса измеряется также базисная сторона с указанной выше точностью. На концах каждой базисной стороны в Т. 1-го и 2-го классов выполняют астрономические определения широты и долготы с погрешностью не более ╠ 0,4 » , а также азимута с погрешностью около ╠ 0,5 » . Кроме того, астрономические определения широты и долготы выполняют и на промежуточных пунктах рядов Т. 1-го класса через каждые примерно 100 км , а по некоторым особо выделенным рядам и значительно чаще.

На основе рядов и сетей Т. 1-го и 2-го классов определяют пункты Т. 3-го и 4-го классов, причём их густота зависит от масштаба топографической съёмки. Например, при масштабе съёмки 1 : 5000 один пункт Т. должен приходиться на каждые 20‒30 км 2 . В Т. 3-го и 4-го классов погрешности измерения углов не превышают соответственно 1,5 » и 2,0 » .

В практике СССР допускается вместо Т. применять метод полигонометрии . При этом ставится условие, чтобы при построении опорной геодезической сети тем и др. методом достигалась одинаковая точность определения положения пунктов земной поверхности.

Вершины треугольников Т. обозначаются на местности деревянными или металлическими вышками высотой от 6 до 55 м в зависимости от условий местности (см. Сигнал геодезический ). Пункты Т. в целях долговременной их сохранности на местности закрепляются закладкой в грунт особых устройств в виде металлических труб или бетонных монолитов с вделанными в них металлическими марками (см. Центр геодезический ), фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.

Координаты пунктов Т. определяют из математической обработки рядов или сетей Т. При этом реальную Землю заменяют некоторым референц-эллипсоидом , на поверхность которого приводят результаты измерения углов и базисных сторон Т. В СССР принят референц-эллипсоид Красовского (см. Красовского эллипсоид ). Построение Т. и её математическая обработка приводят к созданию на всей территории страны единой системы координат, позволяющей ставить топографо-геодезические работы в разных частях страны одновременно и независимо друг от друга. При этом обеспечивается соединение этих работ в одно целое и создание единой общегосударственной топографической карты страны в установленном масштабе.

Лит.: Красовский Ф. Н., Данилов В. В., Руководство по высшей геодезии, 2 изд., ч. 1, в. 1‒2, М., 1938‒39; Инструкция о построении государственной геодезической сети СССР, 2 изд., М., 1966.

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Источник

Триангуляция — построение, метод и сущность

Известно, что триангуляция как геодезический термин означает способ создания геодезических сетей. Да, это так. Но следует начать с другого.

Изначально с возникновением потребности человека в познании, обычное мышление приводит его к накоплению определенного багажа знаний. С развитием научного мышления все эти знания систематизируются, в том числе разъясняются на основе фактов, явлений и доказательств. Применяя теоретические предположения на практике, возникают своего рода критерии истины. То есть имеют ли подтверждения практическим путем все те предположения, которые с помощью определенных способов дают конкретный результат. Пожалуй, одним из таких научных методов, решающих задачу по высокоточному измерению больших расстояний между пунктами на земной поверхности с построением примыкающих друг к другу треугольников и измерений внутри них стал способ триангуляции.

Первым кто изобрел и применил метод триангуляции (1614-1616), был великий голландский ученый Виллеброрд Снелл (Снеллиус). В те годы уже были предположения о том, что Земля является планетой в космическом пространстве и имеет форму сферы (из космологии Джордано Бруно 1548-1600). Установление точных размеров планеты имело большое практическое значение по ее освоению в дальнейшем. Вот для этого в Нидерландах через постройку ряда треугольников были впервые выполнены градусные измерения дуги меридиана способом триангуляции. Что имеется ввиду. Выполнив измерения между жесткими геодезическими пунктами с разностью широт между ними в один градус (у Снеллиуса 1º11´30″) способом триангуляции и получив конкретное расстояние дуги, голландский математик обычным расчетом мог получить длину всей окружности меридиана. Очевидно, что вычислить радиус Земли, приняв ее фигуру за форму шара (эллипса), оставалось делом техники.

В завершение исторического экскурса можно выделить взаимосвязанность и выборность научных познаний для будущего практического применения человеком. И не удивительно, что изобретение способа триангуляции произошло именно в Нидерландах, которые на тот момент считались ведущей морской державой с потребностью новых познаний в навигации, географии, астрономии и конечно геодезии.

Сущность метода

Триангуляция заключается в определении пространственного местоположения специально закрепленных на местности геодезических пунктов в вершинах целого ряда треугольников. Изначально, с высокой степенью точности (до долей секунд) определяют азимуты исходных направлений ab, ba, mn, nm (рис.1.Триангуляционный ряд треугольников по меридиану). Следующим этапом будет определение астрономических координат (широты и долготы) в пунктах измерений азимутов двух исходных базисов. В каждой паре жестких сторон (ab, mn) координаты измеряются только в одной точке, например a, m (рис.1). При этом следует обратить особое внимание на определение астрономических широт в ряду треугольников, расположенных по направлению меридианов. При измерениях в треугольниках, сформированных вдоль параллелей, необходимо уделить должное внимание определению астрономических долгот. Далее производят измерения длин двух базисных сторон (ab, mn). Эти стороны имеют сравнительно не большие длины (порядка 8-10 км). Поэтому их измерения более экономичные и точные относительно сторон cd, tq, составляющих расстояния от 30 до 40 км. В следующую очередь выполняется переход от базисов ab, mn через угловые измерения в ромбах abcd и mntq к сторонам cd, tq. А затем последовательно практически в каждой вершине треугольников cde, def, efg и других измеряются горизонтальные углы до примыкания к следующей основной стороне tq всего ряда треугольников. Через измеренные углы треугольника с измеренной базисной или вычисленной основной стороной последовательно вычисляются все другие стороны, их азимуты и координаты вершин треугольников.

Рис.1. Триангуляционный ряд треугольников по меридиану.

Триангуляционные сети

После первого применения градусного измерения дуги Снеллиусом триангуляционный метод становится основным способом в геодезических высокоточных измерениях. С XIX века, когда триангуляционные работы стали более совершенными с его помощью стали формироваться целые геодезические сети, строящиеся вдоль параллелей и меридианов. Самая знаменитая из всех известна под наименованием геодезической меридианной дуги Струве и Теннера (1816-1852) в последствие зачислена в мировое наследие по ЮНЕСКО. Ее триангуляционный ряд протянулся по Норвегии, Швеции, Финляндии и России от Северного Ледовитого океана до Черного моря в устье Дуная и составил дугу в 25º20´(рис.2).

За основу геодезических сетей триангуляции в нашей стране принята схема профессора Ф.Н.Красовского (рис.3). Ее суть заключается в применении принципа построений от общего к частному. Изначально закладываются вдоль меридианов и параллелей пункты, образующие ряды треугольников протяженностью в пределах 200-240 км. Длины сторон в самих треугольниках составляют 25-40км. Все астрономические измерения азимутов, координат (широт и долгот) выходных точек на пунктах Лапласа (1) и промежуточных астрономических точках (2), высокоточные базисные (3) геодезические измерения и в каждой точке этой цепи должно соответствовать установленным требованиям I класса точности (рис.3). Замкнутый полигон из четырех триангуляционных рядов представляет собой фигуру, напоминающую квадрат с периметром равным ориентировочно около 800 км. Через центральные части первоклассных рядов триангуляции устраиваются в направлении друг к другу основные ряды триангуляционной сети II класса (рис.3) соответствующей точности. Базисные длины сторон в этих рядах не измеряются, а принимаются базисы со сторон триангуляции I класса. Аналогично отсутствуют и астрономические пункты. Возникшие четыре пространства заполняются сплошными триангуляционными сетями и II, и III классов.

Рис.3.Государственные сети триангуляции.

Безусловно описанная схема развития сетей триангуляции по Красовскому не может закрыть всю территорию страны ввиду понятных причин больших лесных и не заселенных территорий страны. Поэтому с запада на восток вдоль параллелей были проложены отдельные ряды первоклассной триангуляции и полигонометрии, а не сплошная триангуляционная сеть.

Достоинства триангуляции

В развитии геодезической науки и ее практического применения очевидны достоинства триангуляционного способа измерений. С помощью этого универсального метода возможно:

определение положения геодезических точек на значительно удаленных расстояниях;
выполнение основных работ по строительству геодезических сетей на всей территории страны;
обеспечение основой всех топографических съемок;
выстраивание через основные геодезические работы различных систем координат;
производство инженерных и изыскательских работ;
периодическое определение размеров Земли;
изучение перемещений земной поверхности.

Источник