Что такое способ стокса

Как определить вязкость жидкости методом Стокса?

Формулу определения вязкости Стокс вывел ещё в 1851 году.

Он получил выражение, описывающее действие силы трения (лобового сопротивления) на круглый объект, движущийся в вязкой жидкости с небольшим числом Рейнольдса.

Чтобы понять, как определять вязкость жидкости методом Стокса необходимо узнать теоретическое описание процесса, вывод формулы и сам описание самого метода.

Всё это и конкретные методы описаны далее в статье.

Содержание статьи

Что такое вязкость

Сама по себе вязкость это свойство жидкости сопротивляться сдвигу слоев. Такой сдвиг выражается в том, что при относительном перемещении слоёв жидкости тот слой, что движется медленнее тормозит слой, который движется быстрее и наоборот.

Вязкость проявляется в наличии между молекулами жидкости сил притяжения, которые пытаются сдерживать движение слоев при перемещении одной части жидкости относительно другой.

По природе все жидкости являются вязкими, потому что между молекулами существуют силы притяжения и отталкивания. Если один слой жидкости вывести из равновесия и сдвигать его относительно другого с некоторой скоростью, то силы взаимного притяжения молекул будут пытаться тормозить это движение.

Движение тела в жидкой среде

Когда твердое тело попадает в жидкость, оно сталкивается с некоторым сопротивлением. Происхождение сил сопротивления жидкости в этом случае может быть объяснено двумя разными механизмами.

Механизм №1 — За твердым телом нет вихрей

Если скорость движения твердого тела маленькая и за ним не образовывается завихрений, то силы сопротивления жидкости характеризуются только вязкостью.

В таком случае слои жидкости, которые прилегают к этому твердому телу, движутся вместе с ним. Но слои жидкости, граничащие с первыми слоями, тоже приходят в движения из-за сил молекулярного притяжения (сцепления).

Таким образом образуются силы, которые затормаживают относительное движение твердого тела в жидкости.

Механизм №2 — При движении тела образуются вихри

Завихрения вокруг твердого тела образуются из-за различия скоростей движения жидкости перед телом и за ним. При этом давление в стационарном потоке жидкости изменяется таким образом, что в области вихрей оно существенном меньше.

Разность давлений в областях перед твердым телом и за ним создает противоположную по направлению движения силу лобового сопротивления жидкости. Эта сила тормозит движение твердого тела.

Сила сопротивления

В случае, когда движение твердого тела в жидкости происходит без образования вихрей, т.е. медленно, сила сопротивления образуется по первому из двух описанных механизмов.

Для тел круглой формы, согласно формуле Стокса, сила сопротивления будет равна:

где μ – вязкость жидкости;
r – радиус шарика;
υ – скорость равномерного движения шарика.

Условие использования формулы

Существует несколько ограничений для применения формулы Стокса.
1. вязкая среда не ограничена стенками и находится в покое
2. скольжений на границах с твердым телом нет
3. движение жидкости ламинарное
4. радиус круглого тела намного больше, чем длина среднего пробега молекул жидкой среды

Формула вязкости

Рассмотрим конкретный случай, когда на шар, движущийся в жидкости действуют три силы:
F_T – сила тяжести;
F_A – сила Архимеда (выталкивающая сила);
T_C – сила лобового сопротивления.

Для круглого шарика сила тяжести будет:

где r –радиус шара;
ρ – плотность шара;
ρ₀ – плотность жидкости;
g – ускорение свободного падения;
υ – скорость равномерного движения шарика;
μ – вязкость жидкости.

В жидкости выталкивающая сила и сила тяжести постоянны. Сила лобового сопротивления пропорциональна скорости движения шарика и на первых этапах она существенно меньше силы тяжести.

При дальнейшем движении шарика наступает момент, когда все три силы уравновешиваются и тогда:

или подставляя формулы

таким образом, определение коэффициента вязкости жидкости методом Стокса сводится к формуле

Определение вязкости методом Стокса

Для того чтобы определить вязкость методом Стокса используют высокий сосуд цилиндрической формы.

На сосуд наносят метки А и В. Такие метки располагаются на заведомо известном расстоянии l друг от друга.

Затем в сосуд наливают исследуемую жидкость выше верхней метки А на 4 – 5 сантиметров. Это необходимо для того, чтобы во время прохождения шариком первой метки его скорость можно было считать установившейся.

Далее шарик бросают в сосуд и секундомером определяют время за которое он проход расстояние от метки А до метки В.

Учитывая, что скорость это отношения длины пути ко времени, т.е.:

и заменяя радиус шарика его диаметром d и определяет коэффициент вязкости жидкости методом стокса

Указанная выше формула применимо в тех случаях, когда шар падает в безграничной среде. Если он падает вдоль оси трубки диаметром R0 (как в этом случае) необходимо ввести поправки на радиус сосуда.

При падении шара радиусом r в трубе радиусом R₀ и высотой h формула будет выглядеть

Исходя из всего вышесказанного получаем, что определение вязкости жидкости методом Стокса требует значения таких параметров, как:
плотность материала шарика;
плотность жидкости;
радиус шарика;
радиус сосуда;
скорость движения шарика.

Видео про методы определения вязкости

Вязкость – это важная характеристика жидкой среды. Её необходимо учитывать при перекачке жидкостей и газов по трубопроводам, смазке машин и механизмов, разливке расплавленных металлов.

Для определения вязкости используют специальные приборы вискозиметры и специальные методы определения. Каждый из методов определения вязкости характеризуется своим набором условий применения.

Но независимо от метода общими остаются:
1. результат измерение не должен зависеть от линейных размеров вискозиметра.
2. не должно быть пристеночного скольжения жидкости.
3. поток жидкости в используемом вискозиметре должен быть ламинарным.

Источник

Что такое способ стокса

Лабораторная работа № 204

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА

Цель работы: изучить метод Стокса, определить коэффициент динамической вязкости глицерина.

Приборы и принадлежности:

стеклянный цилиндрический сосуд с глицерином,

1. ВЯЗКОСТЬ ЖИДКОСТИ. ЗАКОН СТОКСА

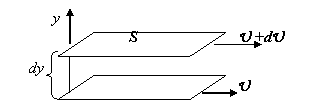
В жидкостях и газах при перемещении одних слоев относительно других возникают силы внутреннего трения, или вязкости, которые определяются законом Ньютона:

(1)

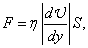
где h — коэффициент внутреннего трения, или коэффициент динамической вязкости, или просто вязкость; 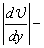модуль градиента скорости, равный изменению скорости слоев жидкости на единицу длины в направлении нормали (в нашем случае вдоль оси y ) к поверхности S соприкасающихся слоев (рис. 1).

Согласно уравнению (1) коэффициент вязкости h в СИ измеряется в Па × с или в кг/( м × с ).

Механизм внутреннего трения в жидкостях и газах неодинаков, т.к. в них различен характер теплового движения молекул. Подробное изложение вязкости жидкости рассмотрено в работе № 203, вязкости газов – в работе № 205.

Вязкость жидкости обусловлена молекулярным взаимодействием, ограничивающим движение молекул. Каждая молекула жидкости находится в потенциальной яме, создаваемой соседними молекулами. Поэтому молекулы жидкости совершают колебательные движения около положения равновесия, то есть внутри потенциальной ямы. Глубина потенциальной ямы незначительно превышает среднюю кинетическую энергию, поэтому, получив дополнительную энергию при столкновении с другими молекулами, она может перескочить в новое положение равновесия. Энергия, которую должна получить молекула, чтобы из одного положения перейти в другое, называется энергией активации W , а время нахождения молекулы в положении равновесия – временем «оседлой жизни» t . Перескок молекул между соседними положениями равновесия является случайным процессом. Вероятность того, что такой перескок произойдет за время одного периода t ₀ , в соответствии с законом Больцмана, составляет

(2)

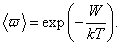
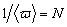
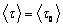
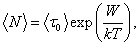
Величина, обратная вероятности перехода молекулы определяет среднее число колебаний, которое должна совершить молекула, чтобы покинуть положение равновесия. Среднее время «оседлой жизни» молекулы . Тогда

(3)

где k – постоянная Больцмана; 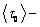средний период колебаний молекулы около положения равновесия.

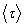
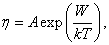
Коэффициент динамической вязкости зависит от : чем реже молекулы меняют положение равновесия, тем больше вязкость. Используя модель скачков молекул, советский физик Я.И.Френкель показал, что вязкость изменяется по экспоненциальному закону:

(4)

где А – константа, определяемая свойствами жидкости.

Формула (4) является приближенной, но она достаточно хорошо описывает вязкость жидкости, например, воды в интервале температур от 5 до 100 ° С, глицерина – от 0 до 200 ° С.

Из формулы (4) видно, что с уменьшением температуры вязкость жидкости возрастает. В ряде случаев она становится настолько большой, что жидкость затвердевает без образования кристаллической решетки. В этом заключается механизм образования аморфных тел.

При малых скоростях движения тела в жидкости слой жидкости, непосредственно прилегающий к телу, прилипает к нему и движется со скоростью тела. По мере удаления от поверхности тела скорость слоев жидкости будет уменьшаться, но они будут двигаться параллельно. Такое слоистое движение жидкости называется ламинарным. При больших скоростях движения жидкости ламинарное движение жидкости становится неустойчивым и сменяется турбулентным, при котором частицы жидкости движутся по сложным траекториям со скоростями, изменяющимися беспорядочным образом. В результате происходит перемешивание жидкости и образуются вихри.

Характер движения жидкости определяется безразмерной величиной Re , называемой числом Рейнольдса. Это число зависит от формы тела и свойств жидкости. При движении шарика радиусом R со скоростью U в жидкости плотностью r _ж

(5)

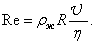
При малых Re ( — 2 мм движется со скоростью 5 — 10 см/ c в вязкой жидкости, например в глицерине, движение жидкости будет ламинарным. В этом случае на тело будет действовать сила сопротивления, пропорциональная скорости

(6)

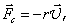
где r – коэффициент сопротивления. Для тела сферической формы

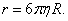
Сила сопротивления шарика радиусом R примет вид:

(7)

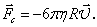
Формула (7) называется законом Стокса.

2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА

Одним из существующих методов определения коэффициента динамической вязкости является метод Стокса. Суть метода заключается в следующем. Если в сосуд с жидкостью бросить шарик плотностью большей, чем плотность жидкости ( r > r _ж ), то он будет падать (рис. 2). На движущийся в жидкости шарик действует сила внутреннего трения (сила сопротивления) 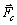, тормозящая его движение и направленная вверх. Если считать, что стенки сосуда находятся на значительном расстоянии от движущегося шарика, то величину силы внутреннего трения можно определить по закону Стокса (6).

Источник