Что такое способ плоскопараллельного движения

Плоскопараллельное перемещение

Плоскопараллельное перемещение — способ перехода от общего положения геометрической фигуры к частному, которое можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекции путем перемещения в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве.

Данный путь лежит в основе метода плоскопараллельного перемещения

Плоскопараллельное перемещение осуществляется путем перемещения геометрической фигуры в новое положение так, чтобы траектория перемещения ее точек находились в параллельных плоскостях. Образно это можно представить в виде перемещения например отрезка вмерзшего в кусок льдины.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой траектории перемещения точек различают:

а) способ параллельного перемещения. Плоскости — носители траекторий перемещения точек параллельны какой-либо плоскости проекции. Траектория — произвольная линия.

б) способ вращения вокруг оси, перпендикулярной к плоскости проекций. Плоскости — носители траектории перемещения точек параллельны плоскости проекции. Траектория — дуга окружности, центр которой находится на оси,перпендикулярной плоскости проекции;

в) способ вращения вокруг оси, параллельной плоскости проекции (вращение вокруг линии уровня);

Плоскости — носители траектории перемещения точек перпендикулярны данной линии уровня. Траектория — дуга окружности, центр которой находится на линии уровня.

г) способ вращения вокруг оси, принадлежащей плоскости проекции (вращение вокруг следа плоскости);

Плоскости — носители траектории перемещения точек перпендикулярны данному следу плоскости. Траектория — дуга окружности, центр которой находится на следе плоскости.

Источник

Что такое способ плоскопараллельного движения

В отличие от способа замены плоскостей проекций, когда данный объект оставался неподвижным, а плоскости проекций изменялись, можно добиться того же результата обратным путем. Оставив плоскости проекций неподвижными, можно перемещать объект в пространстве как неразрывную систему до желаемого положения.

Такое перемещение объекта в пространстве можно выполнить с помощью плоскопараллельного движения.

Плоскопараллельным движением объекта в пространстве называется такое его перемещение, при котором все точки объекта перемещаются в плоскостях, параллельных между собой.

При этом совершенно безразличен вид траектории перемещения точек объекта от исходного до частного положения. Простым примером плоскопараллельного движения является вращение объекта вокруг проецирующей оси. При этом точки описывают окружности в плоскостях, перпендикулярных к оси вращения и, следовательно, параллельных между собой.

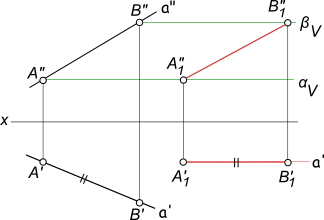
При решении задач чаще всего применяют плоскопараллельное движение относительно одной из плоскостей проекций. При этом все точки объекта перемещаются в плоскостях уровня, то есть в плоскостях, параллельных плоскостям проекций. Отсюда следует, что при плоскопараллельном движении относительно плоскости проекций П₁ все точки объекта перемещаются в горизонтальных плоскостях уровня, а при плоско-параллельном движении относительно П₂ – во фронтальных плоскостях уровня (рис. 132). .

Теорема. Если объект совершает плоскопараллельное движение относительно плоскости проекций П₁, то фронтальные проекции его точек будут двигаться по прямым, перпендикулярным к линиям связи; при этом горизонтальная проекция объекта движется по плоскости проекций, оставаясь равной самой себе. Для доказательства теоремы рассмотрим плоскопараллельное движение отрезка [AB]([A₁B₁][A₂B₂]) относительно плоскости П₁ (рис. 133). Точка A перемещается в плоскости α(α₂)||П₁, точка B – в плоскости β(β₂)||П₁. Следовательно, фронтальные проекции точек A₂ и B₂ будут двигаться по прямым – следам плоскостей движения точек α₂ и β₂: A ∈α, A₂∈α₂ но α₂⊥ (A₁A₂), значит (A₂A’₂)⊥(A₁A₂). Но плоскости α и β являются горизонтальными плоскостями уровня и, следовательно, α₂ ||β₂: β₂⊥(B₁B₂), значит (B₂B’₂) ⊥(B₁B₂). Чем и доказывается первая часть теоремы.

Для доказательства второй части теоремы проведем через точку A (рис. 134) прямую (AB₀)||[A₁B₁]. В полученном прямоугольном треугольнике AB0B катет (B₀B)=(BB₁) – (AA₁) = const, как разность высот точек A и B или, что то же самое, как разность высот плоскостей α и β. При движении отрезка [AB] величина (B₀B) остается постоянной. Также не изменится при движении отрезок [AB], а следовательно, треугольник AB₀B остается при плоскопараллельном движении отрезка [AB], неизменным, постоянным.

Таким образом, горизонтальная проекция [A₁B₁] отрезка [AB] при плоскопараллельном движении относительно плоскости проекций П₁ будет перемещаться по плоскости П₁, оставаясь все время равной себе.

Аналогичным образом можно доказать справедливость этой теоремы при плоско-параллельном движении объекта относительно плоскости проекций П₂.

Применяя плоскопараллельное перемещение относительно плоскости проекций П₁ как способ преобразования комплексного чертежа, на основании доказанной теоремы поступают следующим образом:

1. Горизонтальную проекцию данного геометрического объекта вычерчивают без изменения, располагая ее на чертеже так, как требуется для решения задачи.

2. Фронтальную проекцию определяют по линиям связи на основании новой горизонтальной проекции.

В случае плоскопараллельного перемещения объекта относительно плоскости проекций П₂ горизонтальные проекции точек двигаются по прямым, перпендикулярным к линиям связи, а фронтальная проекция перемещается по плоскости проекций, оставаясь равной самой себе.

Применяя плоскопараллельное перемещение относительно плоскости проекций П₂ как способ преобразования комплексного чертежа, поступают следующим образом:

1. Фронтальную проекцию данного геометрического объекта вычерчивают без изменения, располагая ее на чертеже желательным образом, так, как требуется для решения задачи.

2. Горизонтальную проекцию определяют по линиям связи на основании новой горизонтальной проекции.

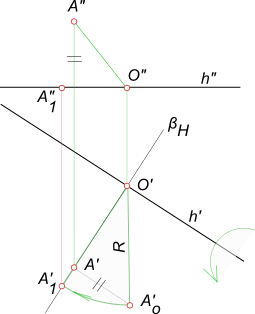
Рассмотрим преобразование отрезка [AB] общего положения в положение фронтальной линии уровня, а затем в положение горизонтально–проецирующей прямой способом плоскопараллельного движения (рис. 135, 136).

Сначала производится плоскопараллельное движение отрезка [AB] относительно плоскости проекций П1. Для этого новую горизонтальную проекцию отрезка [A₁‘B₁‘]=[A₁B₁] нужно разместить так, как требуется для решения задачи, а именно [A₁‘B₁‘]⊥(B₁ B₂).

Фронтальные проекции точек A₂ и B₂ перемещаются по прямым – следам плоскостей движения точек α₂ и β₂: и определяются по линиям связи на основании новой горизонтальной проекции отрезка [A₁‘B₁‘].

В результате отрезок [AB] переведен в положение фронтальной линии уровня и определены его натуральная величина [A₂‘B₂‘]=/AB/ и угол наклона φ к горизонтальной плоскости проекций П₁.

Далее производится плоскопараллельное движение отрезка AB относительно плоскости проекций П₂. В этом случае фронтальная проекция отрезка располагается так, как требуется для решения задачи, а именно:

Горизонтальная проекция перемещается в плоскости γ(γ₁), γ||П₂ и определяется по линиям связи в соответствии с новой фронтальной проекцией [A₂»B₂»]. Тогда горизонтальной проекцией отрезка будет точка A»₁=B»₁, а сам отрезок займет горизонтально-проецирующее положение, что и требовалось в данной задаче. Рассмотрим определение натуральной величины треугольника ABC способом плоско-параллельного движения (рис. 137).

Данная задача решается в два этапа: сначала плоскость переводится из общего положения в проецирующее, а затем – в положение плоскости уровня

Сначала производится плоскопараллельное движение плоскости α(ABC) относительно плоскости проекций П1. Для этого в плоскости α(ABC) проводится горизонталь h(h₁,h₂) и строится новая горизонтальная проекция плоскости α'(A’B’C’), конгруэнтная проекции α(ABC), так, чтобы горизонталь h'(h’₁,h’₂) стала проецирующей прямой, то есть h’₁ ⊥(A₁A₂). Тогда фронтальные проекции точек A₂, B₂, C₂ будут перемещаться по прямым – следам плоскостей движения точек δ₂, β₂ и γ₂: и определяются по линиям связи на основании новой горизонтальной проекции плоскости α'(A’₁B’₁1C’₁). Новая фронтальная проекция плоскости α’₂(A’₂B’₂C’₂) представляет собой отрезок прямой.

Вторым плоскопараллельным движением, но уже относительно плоскости проекций П2, плоскость α(ABC) преобразуется в горизонтальную плоскость уровня. Для этого строится новая фронтальная проекция плоскости α»₂(A»₂B»₂C»₂) в виде горизонтального отрезка, для которого [C»₂ A»₂] = [C’₂ A’₂] и [A»₂ B»₂] = [A’₂ B’₂]. Новая горизонтальная проекция плоскости α»1(A»₁B»₁C»₁) определяется по линиям связи на основании новой фронтальной проекции плоскости α»2(A»₂B»₂C»₂).

Полученная горизонтальная проекция плоскости α»1(A»₁B»₁C»₁) определяет ее натуральную величину: ∆ A»₁B»₁C»₁= /∆ ABC/.

Источник

57. Способ плоскопараллельного перемещения

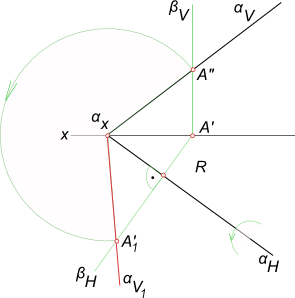
Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение. При этом если точка перемещается в плоскости, параллельной П₁, то ее фронтальная проекция изображается в виде прямой, параллельной оси П₂/П₁. Если же точка перемещается в плоскости, параллельной П₂, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси.

На рис. 107 показан комплексный чертеж прямой АВ. Прямая не параллельна ни одной из плоскостей проекций. Требуется с помощью плоскопараллельного перемещения задать ей такое положение, чтобы она была параллельна одной из плоскостей проекций, например П₂. Через произвольную точку А₁, проводим прямую l₁ параллельную оси П₂/П₁, и от этой точки на прямой откладываем отрезок, равный

А₁В₁. Из точки А₁проводим вертикальную линию связи, а из точки AT, — горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А₂‘. Аналогично проведем вертикальную линию связи из точки В₁до пересечения с горизонтальной линией, проведенной из точки B₂. Новое положение фронтальной проекции точки В получим на пересечении этих линий в точке В₂‘.

После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П₂, а значит, спроецировалась она на эту плоскость в натуральную величину.

Применяя метод плоскопараллельного перемещения, можно решать многие задачи, связанные с определением натуральной величины отрезков, углов, плоских фигур, а также заданием им нужного положения. Однако он связан с изменением положения геометрической фигуры в пространстве. В практике же встречаются задачи, при решении которых при преобразовании комплексного чертежа удобнее оставить положение проецирующего тела неизменным, а изменить положение плоскостей проекций.

Источник

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

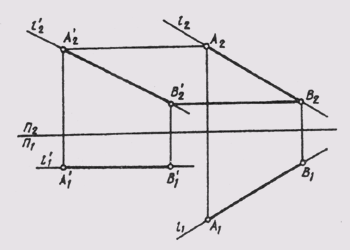
Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A»₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Источник