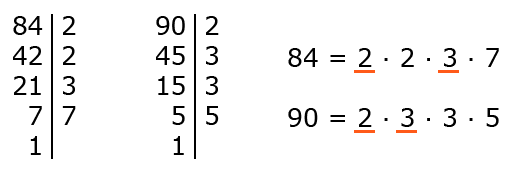Что такое способ евклида

Как найти НОД двух чисел по алгоритму Евклида

Что такое алгоритм Евклида

Алгоритм Евклида — один из наиболее ранних численных алгоритмов в истории. Название было дано в честь греческого математика Евклида, который впервые дал ему описание в книгах «Начала». Изначально назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль. Сегодня чаще используется взятие остатка от деления вместо вычитания, но суть метода сохранилась.

Алгоритм Евклида — это алгоритм, основная функция которого заключается в поиске наибольшего общего делителя (НОД) для двух целых чисел.

Простейшим случаем применения данного алгоритма является поиск наибольшего общего делителя для пары положительных целых чисел. Евклид, автор этого метода, предполагал его использование только для натуральных чисел и геометрических величин. Но позже алгоритм был обобщен и для других групп математических объектов, что привело к появлению такого понятия, как евклидово кольцо.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Понятие НОД

Аббревиатура НОД расшифровывается как «наибольший общий делитель».

Наибольший общий делитель — делитель, который делит без остатка два числа, при этом сам делится без остатка на любой другой делитель исходных двух чисел. То есть это самое большое число, на которое без остатка можно разделить пару чисел, для которых подбирается НОД.

Основная суть алгоритма Евклида

Суть алгоритма заключается в построении ряда следующего вида (при условии, что a больше b):

В нем каждое последующее число — это остаток от деления двух предыдущих, ряд заканчивается, когда остаток от деления становится равным 0 — при условии использования деления.

В нем каждое последующее число является результатом вычитания двух предыдущих, ряд заканчивается, когда частное становится равным 0 — при условии использования вычитания.

Последовательность нахождения НОД при помощи деления:

1. Большее число делится на меньшее.
2. Если результат деления:

• без остатка, то меньшее число и есть НОД;
• с остатком, тогда большее число заменяется на остаток.

1. Переход к пункту 1.

60 / 36 = 1 (остаток 24)

36 / 24 = 1 (остаток 12)

24 / 12 = 2 (остаток 0)

НОД для 60 и 36 равен 12 (делитель).

Последовательность нахождения НОД при помощи вычитания:

1. Из большего числа вычитается меньшее.
2. Если результат вычитания:

• равен 0, то числа равны друг другу и являются НОД;
• не равен 0, в таком случае большее число заменяется на результат вычитания.

1. Переход к пункту 1.

НОД для 60 и 36 равен 12 (уменьшаемое, вычитаемое)

Примеры решения задач с алгоритмом Евклида

Найти наибольший общий делитель для чисел 128 и 96.

128 / 96 = 1 (остаток 32)

Найти наибольший общий делитель для чисел 37 и 17.

37 / 17 = 2 (остаток 3)

17 / 3 = 5 (остаток 2)

3 / 2 = 1 (остаток 1)

2 / 1 = 2 (остаток 0)

Числа 37 и 17 являются простыми, соответственно, их НОД — единица. Совет: перед вычислениями проверяйте таблицу простых чисел.

Источник

Алгоритм Евклида — нахождение наибольшего общего делителя

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Алгоритм нахождения НОД делением

1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6

В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Алгоритм нахождения НОД вычитанием

1. Из большего числа вычитаем меньшее.
2. Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
3. Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6

Функция вычисления НОД

Блок-схема алгоритма Евклида

Примечание. В модуле math языка программирования Python есть функция gcd(), вычисляющая наибольший общий делитель двух чисел.

Источник

В очередной раз о НОД, алгоритме Евклида и немного об истории алгоритмов вообще. Конечно, с примерами на Swift

Алгоритмы – одна из центральных тем в программировании, они повсюду (особенно на собеседованиях, ха-ха).

(Разве можно обойтись в таком посте без «баяна»?)

Одним из самых известных является так называемый алгоритм Евклида – пожалуй, самый распространенный способ нахождения наибольшего общего делителя (НОД) двух целых неотрицательных чисел. С него также зачастую любят начинать изучение (и обучение) соответствующих разделов математики и информатики.

А Дональд Кнут, небезызвестный автор трактата “Искусство программирования” (и не только), и вовсе считает алгоритм первым в истории (по крайней мере, относительно современных определений). Потому что, не смотря на то, что алгоритм был придуман и использовался еще до, собственно, Евклида, который жил в IV-III вв. до нашей эры (он упоминается уже у Аристотеля, жившего веком ранее), Евклид описывает процесс итеративно, что согласуется с современным значением слова.

Само слово “алгоритм” восходит к имени персидского математика Аль-Хорезми, жившего примерно в VIII-IX вв. уже нашей эры. А началом его использования в смысле, близком современному, считается уже лишь XX век, точнее – его первые десятилетия, восход информационных технологий.

Алгоритм Евклида

Любопытства ради предлагаю ознакомиться с евклидовским описанием алгоритма в редактуре Кнута. Оно довольно длинное, поэтому спрятано под катом:

Предложение. Для данных двух положительных целых чисел найти их наибольший общий делитель.

Пусть A и C – два заданных положительных целых числа; требуется найти их НОД. Если число A делится на C, то число C есть общий делитель чисел C и A, поскольку оно делит самое себя. И очевидно, что оно будет и наибольшим делителем, поскольку нет числа большего, чем число C, которое бы делило C.

Но если C не делит число A, то будем непрерывно вычитать меньшее из чисел A и C из большего до тех пор, пока не получим число, которое нацело делит предыдущее вычитаемое. Это должно рано или поздно произойти, потому что, если разность будет равна единице, то единица будет делить предыдущее вычитаемое.

Теперь положим, что E – положительный остаток от деления числа A на C; пусть F – положительный остаток от деления числа C на число E и пусть F делит E. Так как F делит E, а E делит C — F, F также делит C — F. Но оно делит и самое себя, поэтому F делит C, а C делит A — E; поэтому F делит также A — E, но оно делит и E; поэтому F делит A. Следовательно F является общим делителем чисел A и C.

Теперь я утверждаю, что оно является и НОД. Действительно, если F – не наибольший общий делитель чисел A и C, то найдется большее число, которое будет делить оба этих числа. Пусть таким числом будет G.

Так как число G делит число C, а число C – делит A — E, то G также делит число A — E. Число G делит также все число A, поэтому оно делит и остаток E. Но E делит C — F, поэтому G также делит C — F. А число G также делит все число C, так как оно делит и остаток F; таким образом, большее число делит меньшее, а это невозможно.

Таким образом, нет такого числа, большего, чем F, которое бы делило A и C; значит, число F является НОД.

Следствие. Это рассуждение делает очевидным предположение, что всякое число, делящее два числа, делит и их НОД. Ч.т.д.

Описание приводит два способа нахождения НОД – вычитанием и делением. Собственно, и в наши дни широко известны эти два способа реализации алгоритма.

Вот пример функции, написанной на «Swift», реализации первого способа:

Здесь, переиспользования ради, я вынес в отдельную функцию случаи поиска НОД, когда он известен сразу, без необходимости следования какому-либо алгоритму:

(Если два числа равны, то, естественно, их НОД также равен им. Если какое-то из чисел равно нулю, то НОД будет равняться второму числу, т.к. ноль делится любым числом (с результатом, понятное дело, тоже ноль).)

В качестве входных данных могут использоваться только неотрицательные значения. Соответственно, для отрицательных можно использовать те же методы, но взяв числа по модулю. (Да, общий делитель может быть и отрицательным, но мы ищем именно НОД, а положительные числа, очевидно, всегда больше отрицательных.)

А вот так может выглядеть реализация версии алгоритма делением:

Вторая версия в наши дни считается предпочтительней, так как содержит в себе, в среднем, ощутимо меньшее количество шагов. Тем не менее, во времена, когда компьютеры были большие и медленные, операция деления могла быть сама по себе сложной процедурой. И тогда первая версия алгоритма могла оказаться эффективней.

Чтобы немного их сравнить, я произвел несколько замеров с использованием любимого мной метода measure(_:) класса XCTestCase «нативного» фреймворка для тестирования кода в Xcode-проектах XCTest .

В качестве входных данных я использовал массив пар случайных чисел. Замеры производились, естественно, с использованием одного и того же массива для каждого способа. Разброс чисел для пар я взял от нуля до 9999. Замеры производились на количестве вычислений (пар чисел): одно, десять, 100, 1000, 10000, 100000, 1000000 и 10000000. Последнее заставляло ожидать результата уже несколько минут, поэтому на нем я решил остановиться.

Вот простой код генерации входных данных:

Сам замер выглядит, например, так:

А вот так выглядят результаты запуска на моем компьютере:

(Subtraction – вычитание, division – деление.)

В общем, очень хорошо видно, как сильно на современных компьютерах проигрывает метод вычитания.

«Улучшенная» версия алгоритма Евклида

В литературе можно встретить версию алгоритма, в которой одно из чисел на каждом шаге вместо остатка от деления на второе заменяется на разность между этим отстатком и вторым числом, но только в случае, если остаток от деления больше половины второго числа. Реализация этой версии может выглядеть так:

Такая модификация сокращает количество шагов алгоритма, но, судя по результатам замеров на моем компьютере, дополнительные вычисления и проверки на каждом шаге, нейтрализуют это преимущество и даже более:

(Improved – «улучшенная» версия.)

Еще немного о значимости алгоритма Евклида

Алгоритм имеет также геометрическую версию (для нахождения наибольшей меры двух отрезков).

Алгоритм был, конечно, обощен и для нахождения НОД любого количества чисел, не только двух. В двух словах идея такова: если обозначить функцию поиска НОД двух чисел как gcd(a, b), то, скажем, НОД трех чисел gcd(a, b, c) равен gcd(gcd(a, b), c). И так далее, для любого количества чисел НОД находится последовательным вычислением НОД НОД-а предыдущей пары чисел и следующего числа. Хотя, конечно, это касается поиска НОД вообще, а не только алгоритма Евклида.

Существует также обощение алгоритма для нахождения НОД полиномов. Но это уже выходит за рамки этого несложного поста, а в некоторой степени, и моих познаний в математике.

Сложность алгоритма Евклида

Временная сложность алгоритма исследовалась давно, не быстро и гораздо более учеными мужами, чем ваш покорный слуга. Тем не менее, вопрос давно закрыт и ответ получен. Собственно, еще в середине позапрошлого века. Габриэлем Ламе.

Если коротко, то ответ формулируется, собственно, теоремой Ламе, связанной с этим алгоритмом. Количество шагов алгоритма будет равно порядковому номеру ближайшего большего числа Фибоначчи наименьшему из двух чисел входных параметров минус 2. Оперируя чуть более традиционно-математическими обозначениями, то если u > v (и v > 1), то число проходов алгоритма будет равняться n — 2 при v

Источник

Наибольший общий делитель (НОД), свойства и формулы

О чем эта статья:

5 класс, 6 класс

Понятие наибольшего общего делителя

Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общим делителем будет четверка. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4. Но у этой пары чисел есть и другие общие делители: 1, -1 и -4.

Любое число можно разделить на 1, -1 и на само себя. Значит у любого набора целых чисел будет как минимум три общих делителя. Если общий делитель больше 0 — противоположное ему значение со знаком минус также является общим делителем.

Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Например, для 4 и -16 НОД будет 4. Как мы к этому пришли:

Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.

1. Зафиксируем все делители четырех: ±4, ±2, ±1.
2. А теперь все делители шестнадцати: ±16, ±8, ±4, ±3 и ±1.
3. Выбираем общие: это -4, -2, -1, 1, 2 и 4. Самое большое общее число: 4. Вот и ответ.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, -18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, -18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.

Еще один пример. Рассчитаем НОД для 28 и 64.

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

• Например, НОД (25, 25) = 25.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

• Например, НОД (4, 40) = 4, так как 40 кратно 4.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Разложим числа 84 и 90 на простые множители:

Подчеркнем все общие множители и перемножим их между собой:

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Разложим 15 и 28 на простые множители:

Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.

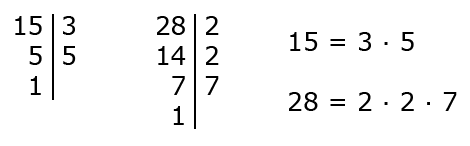
Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Разложим оба числа на простые множители:

Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.

Перемножим общие множители:

НОД (24, 18) =2 * 3 = 6

Ответ: НОД (24, 18) = 6

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

1. Большее число поделить на меньшее.
2. Меньшее число поделить на остаток, который получается после деления.
3. Первый остаток поделить на второй остаток.
4. Второй остаток поделить на третий и т. д.
5. Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

1. 140 : 96 = 1 (остаток 44)
2. 96 : 44 = 2 (остаток 8)
3. 44 : 8 = 5 (остаток 4)
4. 8 : 4 = 2

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

1. Найти наибольший общий делитель любых двух чисел из данных.
2. Найти НОД найденного делителя и третьего числа.
3. Найти НОД последнего найденного делителя и четвёртого числа и т. д.

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник