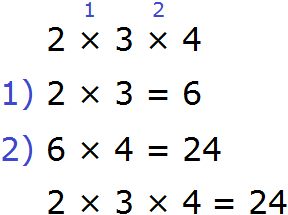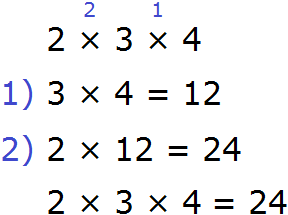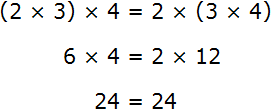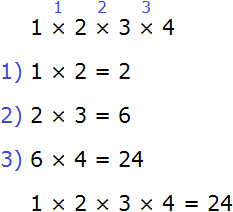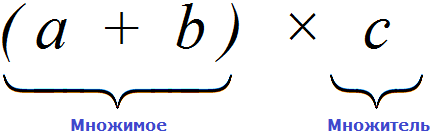Что такое сочетательный способ умножения

Свойства умножения

Переместительное свойство умножения

От перестановки сомножителей местами произведение не меняется.

Следовательно, для любых чисел a и b верно равенство:

выражающее переместительное свойство умножения.

4 · 2 · 3 = 3 · 2 · 4 = 24.

Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.

Сочетательное свойство умножения

Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.

Следовательно, для любых чисел a, b и c верно равенство:

выражающее сочетательное свойство умножения.

3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30

3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.

Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:

25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.

В данном случае можно было вычислить всё последовательно:

25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,

но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.

Распределительное свойство умножения

Сначала рассмотрим распределительное свойство умножения относительно сложения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

выражающее распределительное свойство умножения.

Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

Теперь рассмотрим распределительное свойство умножения относительно вычитания:

Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

Переход от умножения:

соответственно к сложению и вычитанию:

называется раскрытием скобок.

Переход от сложения и вычитания:

называется вынесением общего множителя за скобки.

Источник

Законы умножения

Переместительный закон умножения

Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:

3 + 3 + 3 + 3 = 4 + 4 + 4

Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.

Таким образом, для любых натуральных чисел a и b верно равенство:

выражающее переместительный закон умножения:

От перестановки сомножителей произведение не меняется.

Сочетательный закон умножения

Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:

3 · 2 · 4 = 3 · (2 · 4) = 3 · 8 = 24,

3 · 2 · 4 = (3 · 2) · 4 = 6 · 4 = 24.

Таким образом, для любых натуральных чисел a, b и c верно равенство:

выражающее сочетательный закон умножения:

Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.

Распределительный закон умножения

Для любых натуральных чисел верны равенства:

выражающие распределительный закон умножения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:

Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек. В четырёх рядах всего (3 + 5) · 4 звёздочек.

Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 · 4, а зелёных — 5 · 4. Всего звёздочек 3 · 4 + 5 · 4.

Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:

Например, 6 · (4 — 2) = 6 · 4 — 6 · 2.

Переход от умножения:

соответственно к сложению и вычитанию:

называется раскрытием скобок.

Переход от сложения и вычитания:

называется вынесением общего множителя за скобки.

Источник

Законы математики

В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.

У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.

Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.

В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.

Переместительный закон сложения

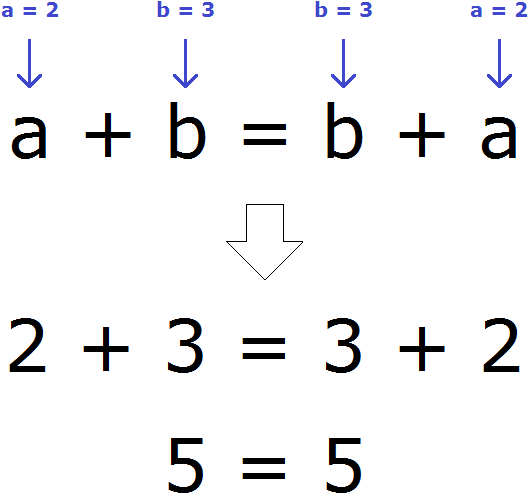
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:

Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.

Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:

Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:

Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3 . Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а , число 3 место b

Сочетательный закон сложения

Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.

Рассмотрим сумму из трёх слагаемых:

Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:

2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10

Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2

2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10

Видно, что в обоих случаях получается один и тот же результат.

Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(2 + 3) + 5 = 2 + (3 + 5)

Запишем сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Переместительный закон умножения

Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.

В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 × 2 = 2 × 5

Запишем переместительный закон умножения с помощью переменных:

Для записи законов в качестве переменных необязательно использовать именно буквы a и b . Можно использовать любые другие буквы, например c и d или x и y . Тот же переместительный закон умножения можно записать следующим образом:

Сочетательный закон умножения

Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

Рассмотрим следующее выражение:

Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:

Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2

Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

Запишем сочетательный закон умножения с помощью переменных:

a × b × с = (a × b) × с = a × (b × с)

Пример 2. Найти значение выражения 1 × 2 × 3 × 4

Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число или число на сумму.

Рассмотрим следующее выражение:

Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:

В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:

8 × 2 = 16

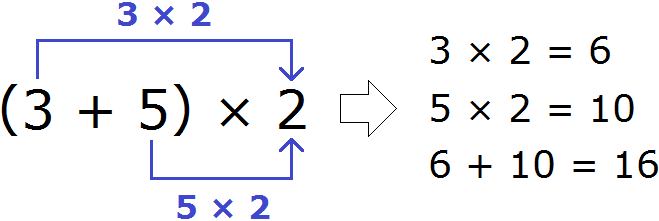
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:

Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

(3 + 5) × 2 = 6 + 10 = 16

Теперь запишем распределительный закон умножения с помощью переменных:

(a + b) × c = a × c + b × c

Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.

Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×

Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b) . Тогда получится, что мы умножаем переменную c на сумму (a + b) . Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:

c × (a + b) = c × a + c × b

Пример 2. Найти значение выражения 5 × (3 + 2)

Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Пример 3. Найти значение выражения 6 × (5 + 2)

Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.

Пример 4. Найти значение выражения 5 × (6 − 2)

Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Пример 5. Найти значение выражения 7 × (3 − 2)

Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

Источник

Свойства умножения и деления

О чем эта статья:

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

• 6 * 5 = 5 * 6 = 30;
• 4 * 2 * 3 = 3 * 2 * 4 = 24.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30

3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

В обратную сторону распределительное свойство умножения относительно сложения звучит так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

В обратную сторону распределительное свойство умножения относительно вычитания звучит так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел

1. Деление на нуль невозможно.
2. Деление нуля на число: 0 : a = 0.
3. Деление равных чисел: a : a = 1.
4. Деление на единицу: a : 1 = a.
5. Для деления переместительное свойства не выполняется: a : b ≠ b : a.
6. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c).
7. Деление произведения на число:
   (a * b) : c = (a : c) * b, если a делится на c;
   (a * b) : c = a * (b : с), если b делится на c;
   (a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c.
8. Деление числа на произведение:
   a : (b * c) = (a : b) * (1 : c) = (a : c) * (1 : b).

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Источник