Что такое синтетический способ разбора задачи

Что такое синтетический способ разбора задачи

На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: аналитический (анализ) и синтетический (синтез). Однако на практике чаще употребляют аналитическо-синтетический разбор задачи.

Под анализом подразумевают способ рассуждений от общего к частному (анализировать – разбивать на составляющие), таким образом при разборе текста задачи от вопроса к данным применяется аналитический способ.

Под синтезом подразумевают способ рассуждений от частного к общему (синтезировать – получать из частей). В задачах это разбор от данных к вопросу, однако, назвать этот метод чисто синтетическим нельзя, т.к. прежде, чем получать метод разбора от данных к вопросу, эти данные нужно предварительно вычленить из задачи, т.е. проанализировать условие задачи.

Непосредственно сам разбор задачи представляет собой цепочку рассуждений, основанных на анализе и синтезе. Организуя разбор задачи вместе с детьми, учитель должен продумать систему специально подобранных вопросов, при помощи которых организуется выбор решения задачи. Эти вопросы не должны быть наводящими, должны вести к самостоятельному выбору решения. Разбор составной задачи заканчивается составлением плана решения. Если вы разбираете задачу с одновременным составлением схемы разбора, то план решения прослеживается прямо по схеме.

Проиллюстрируем различные способы разбора задач на примере следующей задачи: «За день туристы преодолели 100 км. 84 км они проехали автобусом, а остальной путь прошли пешком за 4 часа. Сколько километров туристы проходили за 1 час?» [Б3, №716].

В результате анализа содержания задачи появляется ее краткая запись в виде чертежа:

Направление рассуждений будет следующим:

1) Разбор от вопроса к данным.

Что спрашивается в задаче? (Сколько км туристы проходили за 1 час?) Что нужно знать, чтобы ответить на этот вопрос? (Путь, который прошли туристы и время, которое они затратили на этот путь). Можно ли сразу узнать, сколько км туристы проходили за 1 час? (Нельзя, т.к. мы не знаем путь, который они прошли). Можно ли сразу узнать путь, пройденный пешком? (Можно). Почему вы думаете, что можно? (Так как мы знаем общий путь и путь, пройденный пешком). Далее осуществляется наметка плана решения.

Источник

Синтетический метод решения

Необходимое условие решения сложной задачи – умение решать простые задачи, к которым сводится любая сложная задача. При наличии такого умения вся проблема состоит в том, чтобы найти ту совокупность простых задач, решение которых приведет к выполнению требования основной задачи. Здесь возможны два основных пути поиска решения: синтетический и аналитический.

Как ученики обычно решают сложную задачу? Они берут любое данное в условии задачи и к нему присоединяют какое-либо из остальных данных. Если эти данные образуют простую задачу, то ее решают; если простой задачи не получилось, образуют другую пару данных и в результате решения первой простой задачи получают первое вспомогательное данное. Используя вспомогательное данное и какое-либо из остальных данных основной задачи, решают вторую простую задачу и получают второе вспомогательное данное и т.д. до тех пор, пока не получат такой простой задачи, результат которой является искомым основной задачи.

Это и есть синтетический метод решения задач.

Если основную задачу условно записать: А У, а первую и последнюю из конечной совокупности простых задач, из которых состоит решение основной задачи, обозначить соответственно через а₁ и а_n, то процесс решения задачи синтетическим методом можно записать в виде:

.

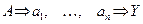
Рассмотрим этот метод на примере.

Задача. Две машины убирают снег за 6 часов. Однажды, после 3 ч совместной работы, первую машину отправили в другой район города, а оставшаяся машина закончила уборку за 5 ч. За сколько часов каждая машина отдельно может выполнить всю работу?

1) Какую часть всей работы выполнили две машины, работая вместе?

2) Какую часть всей работы выполнила вторая машина, после ухода первой?

3) За сколько часов могла бы выполнить всю работу вторая машина, работая отдельно?

4) Какую часть всей работы выполнила вторая машина за 3ч?

5) Какую часть работы выполнила первая машина за 3 ч?

6) За сколько часов могла бы выполнить всю работу первая машина отдельно?

О т в е т : 15ч и 10ч.

Если решение задачи записывается кратко, то необходимо требовать от учеников уметь осознано и правильно формулировать вопросы к каждому действию или пояснять результат полученных вычислений, чтобы исключить случайное совпадение отвлеченных чисел.

Синтетический метод широко применяется не только при решении задач арифметическим способом, но и при решении геометрических задач на вычисление и построение (см. след. пункт).

Рассмотрим краткое решение задачи по геометрии на вычисление.

Задача. В трапеции АВСD диагональ АС перпендикулярна CD и длина проекции CD на основание AD равна 5. Найти длины сторон трапеции, если боковая сторона АВ перпендикулярна основаниям и ВС = 2АВ.

Р е ш е н и е.

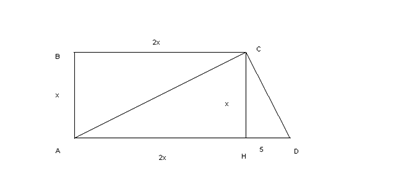
1) Пусть АВ = х. Тогда ВС =АН = 2х, СН = х.

2) В прямоугольном треугольнике АСD СН 2 = АН ∙ НD, или 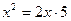. Значит х = 10.

3) АВ= 10, ВС= 20, AD = 25.

4) Из прямоугольного треугольника СHD по теореме Пифагора: .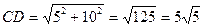

О т в е т : АВ= 10, ВС = 20, СD = 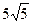, DA = 25.

Основной недостаток синтетического метода – отсутствие какого бы ни было критерия в вопросе, с чего, с каких данных начинать решение и какие вспомогательные величины определять, какие простые задачи решать в дальнейшем, чтобы решить основную задачу. Этот метод мало пригоден для отыскания новых решений и слабо способствует научению школьников самостоятельно решать задачи, логически рассуждать, продуктивно мыслить. Пользуясь синтетическим методом, учащиеся нередко выполняют лишнюю работу, а иногда слабый ученик может предложить бессмысленное действие.

Единственное, на что можно в некоторой степени можно опереться, применяя синтетический метод, – это прошлый опыт ученика в решении задач, аналогия, ассоциации, которые может вызвать решаемая задача.

Достоинством синтетического метода является компактность, достигаемая при изложении готовых решений, полученных в процессе синтетического или аналитического поиска.

Несмотря на низкую поисковую и дидактическую эффективность синтетического метода, он пользуется популярностью у школьников и даже учителей, поскольку весьма прост и не требует большого мыслительного напряжения.

Источник

Использование приёмов анализа и синтеза при работе с задачами,как средство развития мышления.
презентация к уроку по математике на тему

Данный материал поможет педагогам развивать логическое мышление младших школьников

Скачать:

Вложение	Размер
ispolzovanie_priyomov_analiza_i_sinteza_pri_rabote_s_zadachamikak_sredstvo_razvitiya_myshleniya.pptx	91.67 КБ

Предварительный просмотр:

Подписи к слайдам:

Использование приемов анализа и синтеза при работе с задачами , как средство развития логического мышления младших школьников Выполнила:Солдатова.К.С

Необходимость развития логического мышления у детей младшего школьного возраста. Сухомлинский наблюдал за ходом мышления детей, и наблюдения подтвердили , «что прежде всего надо научить детей охватывать мысленным взором ряд предметов, явлений, событий, осмысливать связи между ними… Изучая мышление тугодумов, я все больше убеждался, что неумение осмыслить, например, задачу — следствие неумения абстрагироваться, отвлекаться от конкретного. Надо научить ребят мыслить абстрактными понятиями».

Развитие логического мышления в условиях введения ФГОС НОО Развивая своё логическое мышление, мы способствуем работе интеллекта, а интеллект – это гарантия личной свободы человека и самодостаточности его индивидуальной судьбы. Чем в большей мере человек использует свой интеллект в анализе и оценке происходящего, тем в меньшей мере он податлив к любым попыткам манипулирования им извне.

логические универсальные действия: — анализ объектов с целью выделения признаков (существенных, несущественных); — синтез — составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов; — выбор оснований и критериев для сравнения, сериации , классификации объектов; — подведение под понятие, выведение следствий; — установление причинно-следственных связей; — построение логической цепи рассуждений; — доказательство; — выдвижение гипотез и их обоснование.

Решение задач на уроке математики, как средство развития логического мышления младших школьников Как обучать детей нахождению способа решения задачи? Существует немало практических приемов, облегчающих поиск способа решения задачи.

Приемы анализа и синтеза при работе с задачами Аналитический метод. Анализ – логический прием, состоящий в расчленении исследуемого объекта на составные элементы и исследовании каждого из них в отдельности. Он может использоваться многократно.Разбор задачи от вопроса к данным — это суждение, которое состоит в том, чтобы подобрать два числовых значения одной или разных величин таким образом, чтобы дать ответ на вопрос задачи. Одно из значений или оба могут быть неизвестными. Для их нахождения подбираются два других, и так продолжается процесс подбора, пока не приходим к известным числовым значениям величин. В результате такого разбора учащиеся устанавливают зависимость между числовыми значениями величин, расчленяют ее на простые задачи и составляют план ее решения.

Синтетический метод. Синтез – логическая операция установления связи между составными частями исследуемого объекта и изучения его как единого целого. Исследуемый объект называется в требовании задачи, а его элементы описываются в условии. Разбор задачи от числовых данных состоит в том, что к двум числовым данным подбирается вопрос, затем к следующим двум данным, одно из которых может быть результатом первого действия, подбирается следующий вопрос. И этот процесс продолжается, пока не будет получен ответ на вопрос задачи

Аналитико-синтетический метод. Значительно чаще, используется на практике, чем аналитический и синтетический методы. Он сочетает элементы и анализа и синтеза. Так при решении сложной задачи она с помощью синтеза разбивается на ряд более простых задач, а затем при помощи синтеза происходит соединение решений этих задач в единое целое.Обучение учащихся начальных классов рассмотренным методам поиска решения задач сводится к обучению их правильному формулированию вопросов, соответствующих аналитическому или синтетическому методу.При разборе задачи нового вида учитель должен в каждом отдельном случае поставить детям вопросы так, чтобы навести их на правильный или осознанный выбор арифметических действий.

Способы рассуждений при разборе задач На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: аналитический (анализ) и синтетический (синтез). Однако на практике чаще употребляют аналитическо-синтетический разбор задачи.

Многочисленные психологические исследования показали, что анализ выступает в различных формах: анализ- « фильтр » и анализ через синтез. При применении анализа- « фильтра » человек, решающий задачу просто наугад ищет ее решение, пробуя все возможные варианты, отбрасывая ненужные. Анализ через синтез представляет собой основу любого мыслительного процесса, поэтому его использование при решении задач предпочтительнее.

Упражнения Дана задача: « В один магазин привезли 15 ящиков с фруктами, в другой 10 таких же ящиков. В первый магазин привезли фруктов на 60 кг больше, чем во второй. Сколько килограммов фруктов привезли во второй магазин? » Сделайте разбор задачи разными способами с использованием схемы разбора. Выберите наиболее удачный способ ее разбора. Дополните разбор графической иллюстрацией.

Источник

Обучение учащихся решению задач с использование синтетического метода

Мы рассмотрим реализацию описанных методов путей обучения математике посредством использования диалогического метода. Обратимся вначале к задачам, которые решаются с помощью синтеческого подхода.

Просмотр содержимого документа
«Обучение учащихся решению задач с использование синтетического метода»

В данной главе мы рассмотрим реализацию описанных методических путей обучения математике посредством использо­вания диалогического метода. Обратимся вначале к задачам, которые реша­ются с помощью синтетического подхода. Рассмотрим ряд задач.

Задача 1. Катя купила 7 корзин яблок по 10 килограммов в каждой. Кило­грамм яблок она покупала по 30 рублей; переложив все яблоки в меньшие корзины по 5 килограммов в каждую, она продала каждую корзину по 200 рублей. Сколько прибыли получила Катя от продажи всех яблок?

Эта задача решается синтетическим методом, и поэтому начинаем рас­суждать, отталкиваясь от условия. Из условия, нам известно количество кор­зин и килограммов в каждой, значит, мы можем узнать, сколько всего кило­граммов яблок у Кати. Нам также известно, сколько рублей Катя заплатила за килограмм, значит, мы можем найти, сколько она потратила. Далее Катя пе­реложила все яблоки в корзины по пять килограммов и продавала каждую кор­зину яблок по 200 рублей. Зная массу яблок, несложно найти количество кор­зин. Чтобы узнать, сколько Катя получила денег, нужно стоимость каждой корзины умножить на их количество. И наконец, чтобы найти прибыль, нуж­но из тех денег, что Катя получила при продаже, вычесть количество потра­ченных денег.

Учитель: Если мы знаем, что куплено 7 корзин яблок и что в каждой корзине

было по 10 килограммов, что мы можем узнать?

Ребята: Мы можем узнать, сколько всего килограммов яблок (в 7 корзинах).

7 · 10 = 70 (кг) — всего яблок.

Учитель: Далее в задаче сказано, что Катя купила 1 килограмм яблок за 30 рублей, что мы можем найти из этого?

Ребята: Мы можем найти количество денег, потраченных Катей.

70 · 30 = 2100 (руб.) – потратила Катя.

Учитель: Что же потом сделала Катя?

Ребята: Она переложила все яблоки в корзины по 5 кг.

Учитель: А как мы найдем количество этих корзин?

Ребята: Мы знаем, что всего 70 кг яблок. Для того, чтобы найти количество корзин по 5 кг, нужно 70 : 5 = 14 (корзин) по 5 кг получилось у Кати.

Учитель: Что Катя сделала потом с этими корзинами?

Ребята: Она продала их по 200 рублей за каждую. И для того, чтобы найти, сколько денег Катя получила, нужно 14 • 200 = 2800 (руб.) — количество денег, полученных Катей.

Учитель: А как мы найдем прибыль Кати?

Ребята: Нам нужно из денег, которые она получила, вычесть потраченные

деньги, 2800 – 2100 = 700 (руб.) — прибыль Кати.

Ответ: от продажи яблок Катя получила прибыль 700 рублей.

В синтетическом методе решения геометрических задач можно условно выделить: а) непосредственное синтетическое решение несложных геометрических за­дач; б) запись в виде синтетического решения более сложных задач.

а) Непосредственное синтетическое решение несложных геометрических за­дач. Примером таких задач может быть следующая задача.

Задача 2. Найдите смежные углы, если один из них в два раза больше другого?

Мы знаем из условия задачи, что нам даны смежные углы, один из кото­рых в два раза больше другого, значит, один угол мы можем заменить на уд­военный второй. Зная, что сумма смежных углов равна 180°, легко найдем значения неизвестных углов.

Учитель: что мы имеем из условия?

Ребята: из условия задачи мы имеем:  1 и  2 – смежные и  l = 2  2.

Учитель: что требуется найти в задаче?

Ребята: В задаче требуется найти эти смежные углы.

Учитель: А какими свойствами обладают смежные углы?

Ребята: Из свойства 1 можно записать l + 2 = 180° (по определению смежных углов).

Учитель: Если учитывать данное свойство, а также условие задачи, как мож­но найти эти углы?

Ребята: l = 22; 2 + 22 = 180°. Получаем, 2 = 60°; 1 = 120°.

Ответ:  1 = 120° и 2 = 60°.

б) Запись в виде синтетического решения более сложных задач, где появле­ние вспомогательных суждений часто связано с использованием нестандарт­ных математических идей – анализа. Важно, чтобы эти идеи были подготов­лены и учащиеся самостоятельно к ним приходили.

Содержание этих задач можно обсуждать отдельно, а вот форма дея­тельности в них определяется практически чистым синтезом или очень про­стым использованием приема «синтеза через анализ».

Задача 3. Треугольники BCD и АКЕ равны. В Δ АКЕ АК = 20 см,  K =54°,  E = 60°. Найдите соответствующие стороны и углы Δ BCD .

Зная из условия, что треугольники равны, сторону и два угла Δ АКЕ, мы можем определить, какие углы и стороны первого треугольника равны сторонам и углам второго треугольника, и отсюда найти соответст­вующие стороны и углы Δ BCD.

Учитель: Что мы имеем из условия задачи?

Ребята: Из условия задачи мы имеем, что Δ BCD = Δ АКЕ; АК = 20 см;  К = 54°; E = 60°.

Учитель: Какой вывод можно сделать из того, что треугольники равны?

ВС = АК = 20 см (1, 2);

Ответ: АК = 20 см, K = 54°, E = 60°.

Задача 4. В прямоугольном Δ ABC (ВС – гипотенуза) угол В ра­вен 30°. Чему равен угол С?

Зная, что нам дан прямоугольный треугольник, какая сторона является гипотенузой, легко сказать, какой угол равен 90°. А далее, ис­пользуя теорему о сумме острых углов в прямоугольном треугольнике, легко найти искомый угол.

Учитель: Что имеем из условия задачи?

Ребята: Из условия нам дано, что Δ АВС – прямоугольный; ВС – гипотенуза Δ ABC; B = 30°;  C – ?

Учитель: какое следствие можно записать из п. 2?

Ребята: Используя п. 2, можно сразу записать простое следствие  А = 90°.

Учитель: Если А = 90°, то какую теорему можно вспомнить о других углах в этом треугольнике?

Ребята: Здесь можно применить теорему о сумме углов треугольника для прямоугольных треугольников.

 В + C = 90°. Отсюда, мы можем найти: С = 90° –  B = 60°.

Задача 5. Найдите неизвестный угол треугольника, если у него два угла равны 50 ° и 30°.

Зная из условия два угла треугольника, мы, применив теорему о сумме углов треугольника, легко можем найти третий угол.

Решение. Учитель: что нам дано по условию?

Ребята: нам известно, что дан треугольник, два угла которого равны 50° и 30°.

Учитель: Какую теорему вы знаете о сумме углов в треугольнике?

Ребята: мы знаем, что сумма углов в треугольнике равна 180°. Мы можем найти третий угол, 180° – (50° + 30°) = 100°.

Ответ:  С равен 100°.

Задача 6. Найдите углы треугольника, зная, что внешние углы при двух его вершинах равны 120° и 150°.

По условию в треугольнике нам известны только два внешних угла. Но зная, что внешний угол смежен с внутренним при этой вершине и что сумма смежных углов равна 180°, легко найдем два внутренних угла треугольника. А затем по теореме о сумме углов в треугольнике най­дем и третий угол.

Учитель: Что нам дано в задаче?

Ребята: Нам дан треугольник, у которого внешние углы при двух вершинах равны 120° и 150°.

Учитель: Если это внешние углы, что можно о них сказать?

Ребята: Внешний угол смежен с внутренним углом при этой же вершине.

Учитель: А что мы знаем о смежных углах?

Ребята: Сумма смежных углов равна 180°. Значит, мы можем найти B и C : B = 180° – 120° = 60°, C = 180° – 110° = 70°.

Учитель: Хорошо, теперь мы знаем два угла треугольника. Как найти третий

Ребята: По теореме о сумме углов треугольника найдем  А.

A + B + С = 180°, тогда  А = 180° – (В + С),

А = 180° – (60° + 70°) = 50°.

В преподавании математики синтетический метод должен занять важ­ное место. Обучение надо вести так, чтобы учащиеся не только практически научились пользоваться синтетическим методом, но поняли его сущность и особенности, так как владение им очень важно в практической деятельности человека. Синтетическое изложение доказательств отличается исчерпываю­щей полнотой, сжатостью и краткостью. Однако вести все преподавание ма­тематики в таком стиле малоэффективно. Это связано в первую очередь с тем, что для начинающих изучать математику синтетические доказательства кажутся искусственными и непонятными.

Источник