Что такое решить задачу арифметическим способом 5 класс

Решение текстовых задач арифметическим способом

Разделы: Математика

Обучение решению текстовых задач играет важную роль в формировании математических знаний. Текстовые задачи дают большой простор для развития мышления учащихся. Обучение решению задач – это не только обучение технике получения правильных ответов в некоторых типичных ситуациях, сколько обучение творческому подходу к поиску решения, накопление опыта мыслительной деятельности и демонстрация учащимися возможностей математики в решении разнообразных задач. Однако при решении текстовых задач в 5-6 классах чаще всего используется уравнение. Но мышление пятиклассников еще не готово к формальным процедурам, выполняемым при решении уравнений. Арифметический способ решения задач имеют ряд преимуществ по сравнению с алгебраическим потому, что результат каждого шага по действиям нагляднее и конкретнее, не выходит за рамки опыта пятиклассников. Школьники лучше и быстрее решают задачи по действиям, чем с помощью уравнений. Детское мышление конкретно, и развивать его надо на конкретных предметах и величинах, затем постепенно переходить к оперированию абстрактными образами.

Работа над задачей предусматривает внимательное прочтение текста условия, вникания в смысл каждого слова. Приведу примеры задач, которые легко и просто можно решить арифметическим способом.

Задача 1. Для приготовления варенья на две части малины берут три части сахара. Сколько килограммов сахара нужно взять на 2 кг 600 г малины?

При решении задачи на “части” надо приучить наглядно представлять условие задачи, т.е. лучше опираться на рисунок.

1. 2600:2=1300 (г) — приходится на одну часть варенья;
2. 1300*3= 3900 (г) — сахара нужно взять.

Задача 2. На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках вместе стояло 120 книг. Сколько книг стояло на каждой полке?

1) 1+3=4 (части) — приходится на все книги;

2) 120:4=30 (книг) — приходится на одну часть ( книги на второй полке);

3) 30*3=90 (книг)- стояло на первой полке.

Задача 3. В клетке сидят фазаны и кролики. Всего в ней 27 голов и 74 ноги. Узнать число фазанов и число кроликов в клетке.

Представим, что на крышку клетки, в которой сидят фазаны и кролики, мы положили морковку. Тогда все кролики встанут на задние лапки, чтобы дотянуться до нее. Тогда:

1. 27*2=54 (ноги) — будут стоять на полу;
2. 74-54=20 (ног) — будут наверху;
3. 20:2=10 (кроликов);
4. 27-10=17 (фазанов).

Задача 4. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, а в кино – 21, а 5 человек не ходили ни на экскурсию, ни в кино. Сколько человек ходили и на экскурсию, и в кино?

Для анализа условия и выбора плана решения можно использовать “круги Эйлера”.

1. 30-5=25 (человек) – ходили или в кино, или на экскурсию,
2. 25-23=2 (человек) – ходили только в кино;
3. 21-2=19 ( человек) – ходили и в кино, и на экскурсию.

Задача 5. Три утенка и четыре гусенка весят 2 кг 500 г, а четыре утенка и три гусенка весят 2кг 400г. Сколько весит один гусенок?

1. 2500+2400=2900 (г) – весят семь утят и семь гусят;
2. 4900:7=700 (г) – вес одного утенка и одного гусенка;
3. 700*3=2100 (г) – вес 3 утят и 3 гусят;
4. 2500-2100=400 (г) – вес гусенка.

Задача 6. Для детского сада купили 20 пирамид: больших и маленьких – по 7 и по 5 колец. У всех пирамид 128 колец. Сколько было больших пирамид?

Представим, что со всех больших пирамид мы сняли по два кольца. Тогда:

1) 20*5=100 (колец) – осталось;

2) 128-100-28 (колец) – мы сняли;

3) 28:2=14 (больших пирамид).

Задача 7. Арбуз массой 20кг содержал 99% воды. Когда он немного усох, содержание воды в нем уменьшилось до 98%. Определите массу арбуза.

Для удобства решение будет сопровождаться иллюстрацией прямоугольников.

99% вода	1% сухое вещество
98% вода	2% сухое вещество

При этом желательно рисовать прямоугольники “сухого вещества” равными, потому что масса “сухого вещества” в арбузе остается неизменной.

1) 20:100=0,2 (кг) – масса “сухого вещества”;

2) 0,2:2=0,1 (кг) – приходится на 1% усохшего арбуза;

3) 0,1*100=10 (кг) – масса арбуза.

Задача 8. Гости спросили: сколько лет исполнилось каждой из трех сестер? Вера ответила, что ей и Наде вместе 28 лет, Наде и Любе вместе 23 года, а всем троим 38 лет. Сколько лет каждой из сестер?

1. 38-28=10 (лет) – Любе;
2. 23-10=13 (лет) – Наде;
3. 28-13=15 (лет) – Вере.

Арифметический способ решения текстовых задач учит ребенка действовать осознанно, логически правильно, потому что при решении таким способом усиливается внимание к вопросу “почему” и имеется большой развивающий потенциал. Это способствует развитию учащихся, формированию у них интереса к решению задач и к самой науке математике.

Чтобы сделать обучение посильным, увлекательным и поучительным, надо очень внимательно отнестись к выбору текстовых задач, рассматривать различные способы их решения, выбирая оптимальные из них, развивать логическое мышление, что в дальнейшем необходимо при решении геометрических задач.

Научиться решать задачи школьники смогут, лишь решая их. “Если вы хотите научиться плавать, то смело входите в воду, а, если хотите научиться решать задачи, то решайте их”,- пишет Д.Пойа в книге “ Математическое открытие”.

Источник

Конспект урока и презентация по математике для 5 класса «Решение текстовых задач арифметическим способом»

Выбранный для просмотра документ урок 5 текст.задачи..pptx

Описание презентации по отдельным слайдам:

Решение текстовых задач арифметическими способами

Цель Ученики смогут к концу урока решить две задачи на нахождение сравниваемых величин через данную сумму этих величин

Задачи Ученики будут выполнять вычисление с применением переместительного и распределительного свойства Ученики будут решать задачу по известной сумме и сравнению неизвестных величин: «на столько», «во столько» арифметическим способом

Критерии успешности Я умею применять свойства сложения и умножения для быстрого счета Я понимаю условие задачи, могу выделить известные и неизвестные величины Я умею составлять схему к задаче по условию Я умею ставить вопросы для пошагового решения (план) Я умею объяснять свое решение Я умею грамотно сформулировать ответ к задаче

Градации критериев 1. Я умею применять свойства для быстрого счета: любые свойства; только переместительное свойство; вычисляю без применения свойств. 2. Я понимаю условие задачи да да, нонужна помощь нет Я составлю схему к задаче Я ставлю вопросы к задаче (план) Я могу доказать свое решение Я грамотно сформулируюответ Я могу проверить ответ

Устные упражнения 4 ∙ 315 ∙ 25 46 + 347 + 54 8 ∙35 + 8 ∙ 65 101 ∙ 13 (48 + 56) ∕ 8

Устное упражнение На двух полках 40 книг. Сколько на каждой полке книг, если на них книг поровну?

Задача На двух полках 40 книг. Сколько на каждой полке, если на одной на 10 книг больше, чем на другой. Запись условия: 1 полка ———-? Книг > на 10 книг, чем на 2 полка ———? Книг 40 книг Схема 1: Схема 2: 40 I ? I II II ? 40 ? > на 10 ? 10

План решения Уравнять …….. Изменить …….. Найти одно из неизвестных, для чего …….. Найти второе число ……..

Задача За 2 пакета молока и пачку творога заплатили 590 тенге. Пачка творога на 20 тенге дороже, чем пакет молока. Сколько стоит пакет молока и пачка творога?

Задача Барону Мюнхгаузену и его лошади вместе 45 лет. Сколько лет его лошади, если барон старше на 25 лет? Нарисуйте схему к задаче.

Задача В зоопарке всего 35 львов, носорогов, обезьян и крокодилов. Львов столько же, сколько и обезьян, носорогов на 8 больше, чем львов, а крокодилов на 2 меньше, чем львов. Сколько в зоопарке львов, носорогов, обезьян, крокодилов?

Домашнее задание Сб. Ершова К – 5 А1 (4) Б1 (4)

Выбранный для просмотра документ урок 5.docx

Урок математики в 5 классе.

Тема: Решение текстовых задач арифметическими способам

Цель: Ученики смогут к концу урока решить две задачи на нахождение сравниваемых величин через данную сумму этих величин.

Задачи: Ученики будут выполнять устные вычисления с применением переместительного и распределительного свойства

Ученики будут решать задачу по известной сумме и сравнению неизвестных величин: «на столько», «во столько» арифметическим способом.

Я умею применять свойства сложения и умножения для быстрого счета

Я понимаю условие задачи, могу выделить известные и неизвестные величины.

Я умею составлять схему к задаче по условию.

Я умею ставить вопросы для пошагового решения (план)

Я умею объяснять свое решение

Я умею грамотно сформулировать ответ к задаче.

Деятельность на уроке

1Создание мотивации 5 мин

Приветствие. Деление на группы:

Раздать всем стикеры 5 цветов, на них написаны числа от 1 до 20 (количество учеников)

1) все числа, которые делятся на 5: 5, 10, 15, 20.

2) все числа, которые делятся на 4: 4, 8, 12, 16

3) все числа, которые делятся на 3: 3, 6, 9,18

4) все числа меньше 12: 1,2,7,11 5) все числа больше12: 13.14,17,19,

Решение текстовых задач арифметическими способами

Ученики смогут к концу урока решить две задачи на нахождение сравниваемых величин через данную сумму этих величин

а) устные упражнения

Учитель знакомит с целями и задачами урока, раздает таблицы с критериями самооценивания, первая часть заполняются учениками после устного счета.

Выполняют устные вычисления:

4∙315 ∙25; 46+347+54 8∙35+8∙65 ; 101∙13 ; (48+56): 8

Разбор способов рационального счета

1.Я умею применять свойства для быстрого счета: (выбрать свой ответ)

б) только переместительное свойство;

в) вычисляю без применения свойств .

2.

3.Обучение решению задач

В группах обсуждают решение задачи устно: 1. На двух полках 40 книг. Сколько на каждой полке книг, если на них книг поровну.

2 . На двух полках 40 книг. Сколько на каждой полке, если на одной на 10 книг больше, чем на другой.

Обсуждение решений групп.

Запись усло вия:

1 полка——-? книг> на10книг, чем на второй

2 полка———? Всего книг-40

Схема на слайдах

План решения (разобрать фронтально)

Найти одно из неизвестных, для чего…

Найти второе число….

1.

2.На двух полках 40 книг. Сколько на каждой полке, если на одной на 10 книг больше, чем на другой.

1 полка —? Книг > на 10 книг, чем на

2 полка ———? Книг 40

Схема 1 Схема 2

4.Закрепление метода. 15 мин

а)Решение задач в группах, рассмотренным методом:

1.За 2 пакета молока и пачку творога заплатили 590 тенге, пачка творога на 20 тенге дороже, чем пакет молока. Сколько стоит пакет молока и пачка творога?

2. Барону Мюнхгаузену и его лошади вместе 45 лет. Сколько лет его лошади, если барон старше на 25 лет?

3. В зоопарке 35 львов, носорогов, обезьян и крокодилов. Львов столько же, сколько и обезьян, носорогов на 9 больше, чем львов, а крокодилов на 2 меньше, чем львов. Сколько в зоопарке львов, носорогов, обезьян, крокодилов?

Слайды 10-12 Задача 1.

5. Рефлексия. Подведение итогов. 5 мин

Учащиеся заполняют таблицу самооценивания (2 часть) по градации критериев успешности

6. Домашнее задание 2 мин

Записывают домашнее задание

Сборник дидактических материалов

Математика 5, автор Ершова А.П.

Слайд 13

Источник

Урок математики в 5 классе «Арифметические способы решения текстовых задач»

Урок математики в 5 классе «Арифметические способы решения текстовых задач»

Дистанционное обучение педагогов по ФГОС по низким ценам

Вебинары, курсы повышения квалификации, профессиональная переподготовка и профессиональное обучение. Низкие цены. Более 13500 образовательных программ. Диплом госудаственного образца для курсов, переподготовки и профобучения. Сертификат за участие в вебинарах. Бесплатные вебинары. Лицензия.

Урок математики в 5 классе

«Арифметические способы решения текстовых задач»

Солдатова Светлана Анатольевна

учитель математики первой категории

МОУ Угличский физико-математический лицей

Образовательная: повторить, обобщить и систематизировать приёмы решения текстовых задач арифметическим способом.

Воспитательная: формировать личностные качества: сосредоточенность и внимание; настойчивость в достижение цели.

Развивающая: развивать познавательные интересы в процессе решения нестандартных задач, умения владеть математической терминологией, правильно и четко выражать мысль.

. Организационный момент.

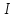
— Сегодня на уроке мы будем решать задачи. Они будут различны по типу, но объединять их будет то, что для решения будет отдано предпочтение арифметическому способу. А так как тема предыдущего урока –«Среднее арифметическое», то на уроке будут разобраны задачи на эту тему.

. Устный упражнения:

– Несколько задач я предлагаю вам решить устно, т.к. для их решения не требуется сложных вычислений, а способы решения вам уже знакомы.

а) (Задача-шутка) Шёл старик в Москву, повстречал 7 старушек: у каждой из них было по мешку, а в каждом мешке по коту. Сколько существ направлялось в Москву?

б) (Старинная индийская задача) Из четырёх пожертвователей второй дал вдвое больше первого, третий – втрое больше второго, а четвёртый — вчетверо больше третьего, а все вместе дали 132 монеты. Сколько монет дал первый?

132 монеты (на доске краткая запись задачи)

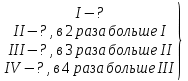
— Что удобно принять за 1 часть?

— Сколько всего монет частей приходится на 132 монеты? (1+2+6+24=33)

132:33=4 (м) – у первого жертвователя.

в) У Олега и Димы вместе72 марки. Сколько марок у каждого, если у Олега на 6 марок меньше?

— Определите тип задачи. (Нахождение двух чисел по их сумме и разности)

— Назовите все возможные способы решения данной задачи.

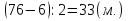
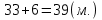
1способ: – у Олега.

— у Димы.

(используется понятие «удвоенное меньшее число»)

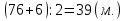
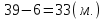
2 способ: — у Димы.

— у Олега.

(используется понятие «удвоенное большее число»)

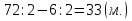
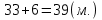
3 способ: — у Олега.

— у Димы.

(используются понятия «полусумма» и «полуразность», так называемый «старинный способ»)

Решение задач по теме «Среднее арифметическое».

а) Настя и Ксюша поделили грибы поровну. У каждой стало по 22 гриба. Сколько грибов набрала каждая, если первоначально у Насти было на 8 грибов больше?

— Какие способы решения вы предлагаете?

— Какой способ самый рациональный по вашему мнению? (среднее арифметическое – это полусумма для двух чисел).

1) (г.) — полуразность.

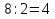
Ответ: 26 грибов, 18 грибов.

б) Среднее арифметическое трёх чисел 0,43. Первое число в 1,5 раза больше второго, а третье в 1,8 раза больше второго. Найдите первое число.

1) (г.) – приходится на сумму трёх чисел.

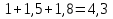
2) – число.

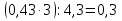
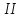
3) – число.

. Задачи на «предположение»

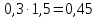
а) (Старинная китайская задача). В клетке находятся 35 фазанов и кроликов. Известно, что у них 94 ноги. Узнайте число фазанов и число кроликов.

— Предположим, что в клетке сидели бы только фазаны. Сколько ног имели бы 35 фазанов? (дети записывают решение в тетради, а учитель на доске)

1) 2 35=70(н.) – если бы было 35 фазанов

— Почему ног больше? (Среди них есть кролики, у которых 4 ноги).

— Если мы одного фазана заменим на кролика, на сколько увеличится количество ног?

2) 4-2=2(н) — на столько ног больше у одного кролика, чем у одного фазана.

— А на сколько ног всего больше?

3) 94-70=24(н.) на столько всего больше ног.

Как узнать количество кроликов?

4) 24:2=12 — кроликов.

5) 35-12=23 – фазанов.

Ответ: 12 кроликов, 23 фазана.

-Есть очень интересное рассуждение, найденное в старых источниках. Представьте, что на верх клетки, в которой сидят фазаны и кролики, мы положим морковку. Все кролики встанут на задние лапки, чтобы дотянуться до морковки.

— Сколько ног в этот момент будут стоять на земле?

— А где остальные?

— Сколько же кроликов?

— Сравните наше рассуждение с записью решения в тетради.

— А теперь попробуйте самостоятельно решить следующую задачу.

б) В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе

19 голов и 46 ног?

30 голов и 74 ноги? (по вариантам, 2 человека у доски с последующей проверкой)

1)2 19=38(н.) – если бы все были куры.

2) 46-38=8(н) — на столько ног больше.

Ответ: 4 овцы, 15 кур.

1)2 30=60(н.) – если бы все были куры.

2) 74-60=14(н) — на столько ног больше.

Ответ: 7 овец, 23 куры.

1) (г.) – приходится на сумму трёх чисел.

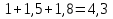
2) – число.

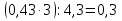
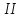
3) – число.

. Разные задачи (старинные)

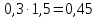
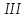
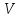
а) Лошадь вместе с седлом стоит 235 р., лошадь вместе со сбруей стоит 250 р., сбруя вместе с седлом стоит 135 р. Сколько стоит лошадь, сколько сбруя и сколько седло?

1) 250+235+135=620(р.) — стоят 2 лошади, 2 сбруи и 2 седла.

2) 620:2 =310(р.) – стоит лошадь, седло и сбруя.

3) 310-235=75(р.) – стоит сбруя.

4) 250-75=175(р.) – стоит лошадь.

5) 235-175=60(р.) – стоит седло.

Ответ: 175 р., 75.р., 60 р.

б ) Крестьянин хочет купить лошадь и для этого продаёт рожь. Если он продаст 15 ц ржи, то ему не хватит для покупки лошади 80 р., а если он продаст 20 ц ржи, то у него останется 110 р. Сколько стоит лошадь?

2) 80 +110=190(ц) стоят 5ц ржи.

3)190:5=38(р.) стоит 1ц ржи.

4) 38 20-110=650(р.) – стоит лошадь.

. Подведение итогов.

Домашнее задание.

1) На лугу паслось несколько коров. У них ног на 24 больше, чем голов. Сколько коров паслось на лугу ?

2) Старинная задача. За 1000 р. Я купил 44 коровы – по 18 р. и по 26 р. Сколько тех и других?

Шевкин А. В. Обучение решению текстовых задач в 5-6 классах. – М.: Галс плюс,1998.

Источник