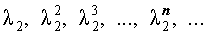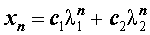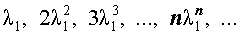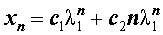Что такое рекуррентный способ задания последовательности

Конспект урока «Рекуррентное задание числовых последовательностей» (9 класс)

Выбранный для просмотра документ Открытый урок Рекуррентное задание числовой последовательности.docx

ТЕМА: Рекуррентное задание числовых последовательностей

Цель урока : познакомить учащихся с рекуррентным способом задания числовой последовательности на примере чисел Фибоначчи и разобрать задачи на преобразование одного задания последовательности в другое.

Воспитательная : продолжить формировать алгоритмическую культуру мышления учащихся на основе дискретного понимания функции.

Развивающая : продолжить развитие навыков и умений работы с формулами задания функции.

Обучающая : научить отличать аналитический способ задания функции от рекуррентного, переводить одно задание функции в другое.

Учебник, компьютер (проектор).

Учащиеся получат представление рекуррентных соотношениях.

Узнают о способе перехода от аналитического задания к рекуррентному.

Научатся использовать рекуррентные формулы для вычисления значений последовательности.

Проверка домашнего задания.

Актуализация темы «Способы задания функции»

Изучение нового материала (работа с презентацией).

Определение рекуррентного соотношения.

Различия аналитического и рекуррентного способа задания.

Определение последовательности Фибоначчи

Онтологическая интерпретация чисел Фибоначчи.

Свойства последовательности Фибоначчи.

Решение заданий из учебника

Приветствие, проверка присутствующих. Объявление темы урока, объяснение хода урока.

2. Проверка домашнего задания: № 16.6, 15.41.

3. Актуализация темы «Способы задания функции»

( Презентация ) Вспомнить в процессе беседы с учащимися какие бывают способы задания функции: аналитический, словесный, табличный, кусочный. Обосновать на базе дискретной природы числовых последовательностей возможность установления связи текущего члена последовательности с предыдущим.

4. Изложение нового материала.

1. Определение рекуррентного соотношения

Опр. ( презентация ) Говорят, что последовательность задана рекуррентным соотношением, если указана формула, в одной части которой находится только n — ый член последовательности, а в другой — буквенное выражение, содержащее предыдущие члены последовательности, в котором аргумент не участвует в вычислениях значения функции.

2. Различия аналитического и рекуррентного способа задания .

Различие состоит в том, что при аналитическом способе вычисления n — го члена в буквенном выражении имеется аргумент, с помощью которого можно сразу получить результат, не зная при этом значений остальных членов последовательности. При рекуррентном способе вычисления n — го члена обязательно надо знать значения предыдущих членов, начиная с первого. При этом в формуле рекуррентного соотношения аргумент присутствует только как индекс нумерации и в вычислениях не используется. Образно говоря, функция натурального аргумента задана зависимостью от начального и получаемого значения той же функции как в «принципе домино».

3. Определение последовательности Фибоначчи

Опр. ( презентация ) Последовательностью Фибоначчи называется числовая последовательность, у которой заданы изначально первый и второй члены, а n — ый член вычисляется как сумма ( n —1)- го и ( n —2)- го членов.

4. Онтологическая интерпретация чисел Фибоначчи.

На Западе впервые эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что: изначально есть новорожденная пара кроликов (самец и самка), со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов, кролики никогда не умирают. Сколько пар кроликов будет через год? ( презентация )

В начале первого месяца есть только одна новорожденная пара (1).

В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1)

В конце второго месяца первая пара рождает новую пару и опять спаривается (2)

В конце третьего месяца первая пара рождает еще одну новую пару и спаривается, вторая пара только спаривается (3)

В конце четвертого месяца первая пара рождает еще одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5)

5. Свойства последовательности Фибоначчи .

Если числа Фибоначчи заданы следующим образом:

тогда справедливы следующие свойства ( презентация ):

5. Решение заданий из учебника

Решение учителем № 15.37, 15.31, 15.20 (а, б), 15.32, 15.21.

Решение учащимися № 15.37, 15.31, 15.20, 15.32, 15.21 (а, б).

Заключительный опрос по изученному материалу:

1) Приведите примеры рекуррентного соотношения

2) Приведите пример последовательности Фибоначчи

3) Запишите рекуррентно арифметическую прогрессию

Источник

Возвратные последовательности:
рекуррентная формула, характеристическое уравнение

Определение возвратной последовательности

Характеристическое уравнение

Общее решение рекуррентного уравнения 2-го порядка

Схема вывода формулы общего члена возвратной последовательности второго порядка

Примеры с решениями

Определение возвратной последовательности

в каждой из которых символами b₁ и q обозначены заданные числа – первый член и знаменатель прогрессии.

Определение . Пусть k – натуральное число. Возвратной (рекуррентной) последовательностью порядка k называют последовательность, для задания которой требуется задать первые её k членов, т.е. числа

а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)

– заданные числа ( коэффициенты рекуррентной формулы ).

Замечание 1 . Числа

называют начальными условиями .

Замечание 2 . Для упрощения вычислений везде в дальнейшем будем рассматривать только случай возвратных последовательностей 2-го порядка, все члены которых являются вещественными числами.

Для задания таких последовательностей требуется задать их первые два члена, то есть вещественные числа x₁ и x₂ , а остальные члены последовательности

xn = q1 xn – 1 + q2 xn – 2 , n > 2 ,

(1)

Характеристическое уравнение

Для того, чтобы получить характеристическое уравнение возвратной последовательности (1), будем искать такие числа λ , при которых последовательность вида

xn = λ n

(2)

удовлетворяет рекуррентной формуле (1).

xn – 1 = λ n – 1 , xn – 2 = λ n – 2 ,

(3)

то при подстановке формул (2) и (3) в формулу (1) возникает уравнение

которое удобно переписать в виде

λ n – q1 λ n – 1 – – q2 λ n – 2 = 0 .

(4)

Если теперь уравнение (4) разделить на λ n–2 , то мы получим квадратное уравнение относительно λ вида:

которое и называют характеристическим уравнением .

Общее решение рекуррентного уравнения второго порядка

В случае, когда характеристическое уравнение имеет два различных вещественных корня λ₁ и λ₂ , каждая из последовательностей

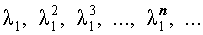
и

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c₁ и c₂ последовательность с общим членом

также удовлетворяет рекуррентной формуле (1).

Числа c₁ и c₂ называют произвольными постоянными .

В случае, когда характеристическое уравнение имеет два совпавших вещественных корня λ₁ = λ₂ , непосредственная проверка показывает, что каждая из последовательностей

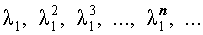
и

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c₁ и c₂ последовательность с общим членом

также удовлетворяет рекуррентной формуле (1).

В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ_{1, 2} = α ± i β, каждая из последовательностей

удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c₁ и c₂ последовательность с общим членом

также удовлетворяет рекуррентной формуле (1).

Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.

Источник

Числовая последовательность

п.1. Формулы числовых последовательностей

Запишем несколько первых чётных чисел и пронумеруем их:

Этот ряд бесконечен, но, глядя на таблицу, его легко задать формулой: \begin \mathrm> \end

Теперь, пользуясь формулой, для любого порядкового номера n мы сможем найти соответствующее чётное число.

Для обозначения членов последовательности и их индексов можно использовать разные буквы: x₁, x₂, . x_m. ; a₁, a₂, . a_k. ; A₁, A₂, . A_s. и т.д.

Например:
Найти 1й, 3й и 4й члены последовательности, заданной формулой \(\mathrm>\) $$ \mathrm< y_1=\frac<1-1><1+1>=0,\ \ y_3=\frac<3-1><3+1>=\frac12,\ \ y_4=\frac<4-1><4+1>=\frac35 > $$

п.2. Задание последовательностей описанием

Последовательность, заданную формулой y_n=2n, можно задать описанием как «последовательность чётных чисел».

Последовательность, заданную формулой \(\mathrm>\), можно задать описанием как «последовательность дробей, числитель которых на 1 меньше индекса, а знаменатель на 1 больше индекса последовательности».

Кроме того, существуют такие последовательности, которые можно задать только описанием.

Например:
1. Последовательность простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

2. Последовательность десятичных приближений числа \(\mathrm<\sqrt<3>>\) по недостатку:

1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,7302050; 1,73020508,…

п.3. Рекуррентные формулы числовых последовательностей

Важнейшим классом числовых последовательностей, которые широко используются в алгоритмах вычислительной математики, являются рекуррентные отношения (от латинского слова recurrere – возвращаться).

Например:
Найти y₅, если y₁ = 1, y_n = 2y_n-1 + 1
Проводим последовательные вычисления:
y₂ = 2y₁ + 1 = 3, y₃ = 2y₂ + 1 = 7, y₄ = 2y₃ + 1 = 15, y₅ = 2y₄ + 1 = 31
Интересно, что, если присмотреться, эту последовательность можно также задать аналитически: y_n = 2 n – 1.

п.4. Свойства числовых последовательностей

Например:
Последовательность квадратов натуральных чисел y_n = n 2 возрастающая:

Например:
Последовательность дробей с индексом в знаменателе \(\mathrm\) – убывающая: $$ 1\gt\frac12\gt\frac13\gt. \gt\frac1n\gt. $$

Например:
Последовательность отрицательных дробей с индексом в знаменателе \(\mathrm\) ограничена сверху числом M = 0: $$ -1\lt 0,\ \ -\frac12\lt 0,\ \ -\frac13\lt 0. \ \ -\frac1n\lt 0, . $$

Например:
Последовательность дробей с индексом в знаменателе \(\mathrm\) ограничена снизу числом M = 0: $$ -1\gt 0,\ \ \frac12\gt 0,\ \ \frac13\gt 0. \ \ \frac1n\gt 0, . $$

Например:
Последовательность дробей с индексом в знаменателе \(\mathrm\) ограничена: $$ 1\gt \frac12\gt \frac13\gt . \gt \frac1n\gt . \gt 0 $$ Верхней границей является M = 1, нижней границей K = 0.

п.5. Примеры

Пример 1. Найдите первые 4 члена последовательности, заданной формулой
a) \(\mathrm<2n-1>>\)

Пример 2. Найдите первые 4 члена последовательности, заданной рекуррентной формулой
a) y₁ = 3, y_n = 3y_n – 1

Пример 3*. Укажите какую-либо формулу для n-го члена числовой последовательности

а) 3, 5, 7, 9, .
Это – последовательность нечётных чисел, для которой:
y_n = 2n + 1

б) 5, -5, 5, -5.
Это – знакопеременная последовательность, для которой модуль всегда равен 5, а знак меняется. Изменение знака можно записать как степень (–1). Учитывая, что нечётные члены последовательности положительные, а чётные – отрицательные, получаем:
y_n = (–1) n+1 · 5

в) \(\mathrm<\frac<1><1\cdot 2>,\ \ \frac<1><2\cdot 3>,\ \ \frac<1><3\cdot 4>. >\)
Это – последовательность дробей, у которых в знаменателе произведение текущего индекса n на следующий индекс (n + 1):
\(\mathrm>\)

г) 2, 5, 10, 17, 26, 37, .
Заметим, что

5 — 2 = 3, 10 — 5 = 5, 17 — 10 = 7, 26 — 17 = 9, .

Каждый последующий член отличается от предыдущего на возрастающее нечётное число. Можем записать рекуррентную формулу:
y₁ = 2, y_n = y_n-1 + (2n –1)

Пример 4*. Пифагор изучал последовательность «треугольных» чисел, которые можно задать следующими геометрическими фигурами:

и т.д.
Задайте эту последовательность 1) рекуррентной формулой; 2) аналитической формулой.

1) Запишем последовательность в явном виде, как это следует из чертежа: $$ \mathrm< y_1=1,\ \ y_2=\underbrace<1>_+2=3,\ \ y_3=\underbrace<1+2>_+3=6,\ \ y_4=\underbrace<1+2+3>_+4=10 > $$ Отсюда получаем следующую рекуррентную формулу: y₁ = 1, y_n = y_n-1 + n

2) Для произвольного члена последовательности:

y_n = 1 + 2 + 3 + . + (n — 2) + (n — 1) + n

Найдём эту сумму. Для этого запишем выражение наоборот:

y_n = n + (n — 1) + (n — 2) + . + 3 + 2 + 1

Источник