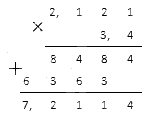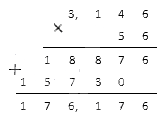Что такое рациональный способ вычисления дробей

Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .

Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).

К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .

Осуществим сложение дробей с разными знаменателями:

6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45

Ответ: 0 , 6 + 5 9 = 1 7 45 .

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .

Решение

Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:

​​​​​​

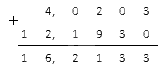
Полученному результату присваиваем знак минус: — 16 , 2133 .

Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55

Ответ: 4 , ( 36 ) — 1 5 = 4 9 55

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .

Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7

Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7

Ответ: 2 7 + — 5 3 7 = — 5 1 7

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа a на нуль есть нуль.

Используя переместительное свойство умножения, получим: 0 · а = 0 .

К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .

Умножение на единицу

Умножение любого рационального числа a на 1 дает число a .

Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .

К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .

Решение

Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .

Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .

Ответ: 0 , 5 · 6 25 = 3 25

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2 , 121 · 3 , 4 = 7 , 2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: — 3 3 8 и 2 1 2

Решение

Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2

Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16

Ответ: — 3 3 8 · 2 1 2 = — 8 7 16

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .

Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления 3 1 3 : — 1 1 6

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .

Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7

Ответ: 3 1 3 : — 1 1 6 = — 2 6 7

Источник

Дробные рациональные выражения

Содержание:

Дробные рациональные выражения

Дробные рациональные выражения — это выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля. Дробные выражения допускают также деление на выражение с переменными. Целые и дробные выражения называют рациональными выражениями.

Рациональная дробь и ее основное свойство

Любое дробное выражение (см. п. 48) можно преобразовать к виду , где Р и Q — многочлены. Такую дробь называют рациональной дробью.

Примеры рациональных дробей:

Основное свойство дроби выражается тождеством справедливым при условиях и здесь R — целое рациональное выражение. Это значит, что числитель и знаменатель рациональной дроби можно умножить или разделить на одно и то же отличное от нуля число, одночлен или многочлен. Например,

Основное свойство дроби может быть использовано для перемены знаков у членов дроби. Если числитель и знаменатель дроби умножить на -1, получим . Таким образом, значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:

Значит,

Например,

Сокращение рациональных дробей

Сократить дробь — это значит разделить числитель и знаменатель дроби на их общий множитель. Возможность такого сокращения обусловлена основным свойством дроби.

Для того чтобы сократить рациональную дробь, нужно числитель и знаменатель разложить на множители. Если окажется, что числитель и знаменатель имеют общие множители, то дробь можно сократить. Если общих множителей нет, то преобразование дроби посредством сокращения невозможно.

Пример:

Сократить дробь

Решение:

Имеем

Значит,

Сокращение дроби выполнено при условии

Приведение рациональных дробей к общему знаменателю

Общим знаменателем нескольких рациональных дробей называют целое рациональное выражение, которое делится на знаменатель каждой дроби (см. п. 54).

Например, общим знаменателем дробей и служит многочлен (х + 2)(х — 2), так как он делится и на х + 2, и на х — 2. Общим знаменателем могут также служить и многочлен 3 и многочлен х (х + 2) (х — 2), и многочлен и т. д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный. Такой простейший знаменатель называют наименьшим общим знаменателем.

В рассмотренном выше примере наименьший общий знаменатель равен (х + 2)(х — 2). Имеем

Приведение данных дробей к общему знаменателю достигнуто путем умножения числителя и знаменателя первой дроби на х — 2, а числителя и знаменателя второй дробей на х + 2. Многочлены х — 2 и х + 2 называют дополнительными множителями соответственно для первой и второй дроби. Дополнительный множитель для данной дроби равен частному от деления общего знаменателя на знаменатель данной дроби.

Чтобы несколько рациональных дробей привести к общему знаменателю, нужно:

1) разложить знаменатель каждой дроби на множители;

2) составить общий знаменатель, включив в произведение все множители полученных в п. 1) разложений; если некоторый множитель имеется в нескольких разложениях, то он берется с показателем степени, равным наибольшему из имеющихся;

3) найти дополнительные множители для каждой из дробей (для этого общий знаменатель делят на знаменатель дроби);

4) домножив числитель и знаменатель каждой дроби на соответствующий дополнительный множитель, привести дроби к общему знаменателю.

Пример:

Привести к общему знаменателю дроби

Решение:

Разложим знаменатели дробей на множители:

В общий знаменатель надо включить следующие множители: , а также наименьшее общее кратное чисел 12, 18, 24, т. е. К (12, 18, 24) = 72. Значит, общий знаменатель имеет вид

Дополнительные множители: для первой дроби для второй дроби для третьей дроби Значит, получаем

Сложение и вычитание рациональных дробей

Сумма двух (и вообще любого конечного числа) рациональных дробей с одинаковыми знаменателями тождественно равна дроби с тем же знаменателем и с числителем, равным сумме числителей складываемых дробей:

Аналогично обстоит дело в случае вычитания дробей с одинаковыми знаменателями:

Пример 1.

Упростить выражение

Решение:

Выполним сложение данных дробей:

Для сложения или вычитания рациональных дробей с разными знаменателями нужно прежде всего привести дроби к общему знаменателю, а затем выполнить операции над полученными дробями с одинаковыми знаменателями.

Пример 2.

Упростить выражение

Решение:

Имеем

Умножение и деление рациональных дробей

Произведение двух (и вообще любого конечного числа) рациональных дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей перемножаемых дробей:

Частное от деления двух рациональных дробей тождественно равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель — произведению знаменателя первой дроби на числитель второй дроби:

Сформулированные правила умножения и деления распространяются и на случай умножения или деления на многочлен: достаточно записать этот многочлен в виде дроби со знаменателем 1.

Учитывая возможность сокращения рациональной дроби, полученной в результате умножения или деления рациональных дробей, обычно стремятся до выполнения этих операций разложить на множители числители и знаменатели исходных дробей.

Пример 1.

Выполнить умножение

Решение:

Использовав правило умножения дробей, получим

Пример 2.

Выполнить деление

Решение:

Использовав правило деления дробей, получим

Возведение рациональной дроби в целую степень

Чтобы возвести рациональную дробь в натуральную степень , нужно возвести в эту степень отдельно числитель и знаменатель дроби; первое выражение — числитель, а второе выражение — знаменатель результата:

Пример 1.

Преобразовать в дробь степень

Решение:

Применив правила возведения в степень дроби и одночлена, получим

При возведении дроби в целую отрицательную степень используется тождество справедливое для всех значений переменных, при которых

Пример 2.

Преобразовать в дробь выражение

Решение:

Преобразование рациональных выражений

Преобразование любого рационального выражения сводится к сложению, вычитанию, умножению и делению рациональных дробей, а также к возведению дроби в натуральную степень. Всякое рациональное выражение можно преобразовать в дробь, числитель и знаменатель которой — целые выражения; в этом, как правило, состоит цель тождественных преобразований рациональных выражений.

Пример:

Решение:

Выполняя действия с рациональными дробями, получим:

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник