Что такое поверхность при задании кинематическим способом
Поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют некоторому заданному уравнению вида F(x,y,z)=0 (рис. 48, а, б, в). Порядок уравнения соответствует порядку поверхности. Порядок поверхности можно определить и геометрически, как порядок кривой, по которой плоскость пересекает поверхность, или как число точек пересечения прямой с поверхностью.


б – гиперболоид однополостный
в – гиперболический цилиндр
Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать свойства поверхности.
Кинематическую поверхность можно рассматривать как непрерывную совокупность последовательных положений линии, перемещающейся в пространстве по некоторым неподвижным линиям. Таким образом, на любой кинематической поверхности можно выделить два семейства линий: семейство образующих и семейство направляющих. Направляющие и образующие обладают следующим свойством: никакие две линии одного семейства не пересекаются между собой, но каждая линия одного семейства пересекает все линии другого.
Рассмотрим формирование конической поверхности (рис. 49). Такая поверхность образована движением прямой образующей l, постоянно проходящей через точку S и во всех своих положениях пересекающей некоторую направляющую кривую m. Если направляющая m – окружность, каждая точка которой равноудалена от вершины S, образуется прямой круговой конус.
Совокупность точек, линий и различных условий, определяющих закон перемещения образующей, называют также определителем поверхности. Например, определителем конуса вращения могут быть ось и образующая или вершина и направляющая линия. Определителем цилиндра вращения может быть ось и образующая (прямая или кривая) или ось и направляющая (окружность). Окружность может быть и направляющей линией цилиндра и его образующей. В начертательной геометрии все поверхности рассматриваются как кинематические, то есть образованные непрерывным перемещением в пространстве какой – либо линии или поверхности.

Поверхности, к которым нельзя применить математические закономерности или поверхности с произвольными образующими называются скульптурными или поверхностями произвольных форм (рис. 50). Такие поверхности обычно задают достаточно плотной сетью линий и точек, принадлежащих этим поверхностям. Совокупность таких линий называется каркасом поверхности. При этом точки, лежащие между линиями каркаса, определяются приближенно.
Одним из наиболее распространенных в промышленности методов конструирования поверхностей является метод конструирования с помощью непрерывного каркаса. Метод каркасного конструирования используется при изготовлении кузовов автомобилей, самолетов и в судостроении, для выполнения штампов при изготовлении поверхностей из листового материала, в топографии, горном и дорожном деле.
Источник
Что такое поверхность при задании кинематическим способом
Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б
Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.
Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.
В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.
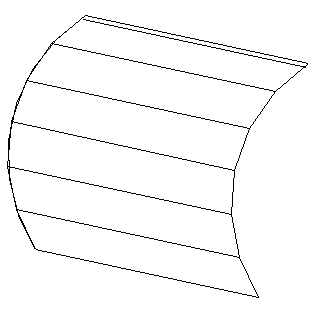
Рисунок 37
На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.
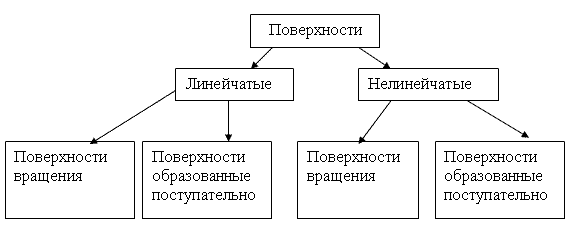
Рисунок 38
Линейчатые поверхности вращения – это конус, цилиндр.
Линейчатые поверхности поступательного движения – все гранные поверхности.
К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.
Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.
Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.
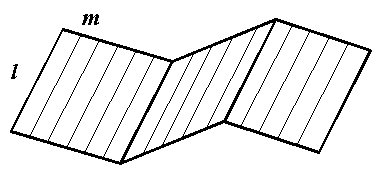
Рисунок 39
Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.
Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.
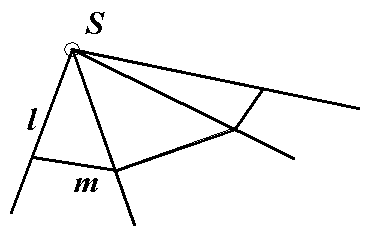
Рисунок 40
Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.
1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?
2. Назовите линейчатые поверхности вращения.
3. Какие нелинейчатые поверхности вы знаете?
4.Какая линия является направляющей у гранных поверхностей, какая является образующей?
5. Как образуется поверхность пирамиды, призмы?
6. Какая призма называется прямой?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Большая Энциклопедия Нефти и Газа
Кинематический способ — образование — поверхность
Кинематический способ образования поверхности связан с понятием определителя поверхности, под которым понимают совокупность независимых условий, однозначно задающих поверхность. [1]
Кинематический способ образования поверхности подводит нас к понятию определителя, под которым мы будем подразумевать необходимую и достаточную совокупность геометрических фигур и связей между ними, которые однозначно определяют поверхность. [2]
Кинематический способ образования поверхности подводит нас к понятию определителя, под которым мы будем подразумевать совокупность независимых условий, однозначно задающих поверхность. [3]
Возможна демонстрация кинематических способов образования поверхностей как на ортогональных проекциях, так и в аксонометрии с изменением параметров определителя поверхности и демонстрация фрагментов технологических процессов формообразования поверхностей элементов деталей. [4]
Возможна демонстрация кинематических способов образования поверхностей как на ортогональных проекциях, так и в аксонометрии с изменением параметров определителя поверхности. Возможна демонстрация фрагментов технологических процессов формообразования поверхностей и различных элементов деталей. [5]
В чем заключается кинематический способ образования поверхностей . Что называют определителем поверхности. [6]
Начертательная геометрия пользуется преимущественно кинематическим способом образования поверхностей . Это означает, что поверхность образуется непрерывным перемещением линии ( образующей) в пространстве по определенному закону. [7]
В современных курсах начертательной геометрии изучается в основном кинематический способ образования поверхностей , когда поверхность образуется в результате перемещения некоторой линии постоянной или переменной формы. При всех своих несомненных достоинствах ( простота, наглядность) этот способ имеет существенные недостатки, связанные со сложностью исследования свойств поверхности в целом. [8]
В начертательной геометрии пользуются, главным образом, кинематическим способом образования поверхностей . [9]
Во многих случаях линия или поверхность параметризуется с использованием понятий каркаса и определителя. В начертательной геометрии применяется кинематический способ образования поверхности . Этот способ подразумевает, что поверхность образуется непрерывным перемещением линии, называемой образующей, в пространстве по некоторому закону. Этот закон может быть определен заданием геометрических условий. Например, образующая перемещается, пересекая неподвижные линии, называемые направляющими. Последними могут быть также плоскости либо поверхности. [10]
Толщины она не имеет, Поверхность есть то, что имеет только длину и ширину ( Эвклид), В общежитии различают поверхности плоские, выпуклые, вогнутые, а в различных разделах математики они имеют более сложную классификацию. В начертательной геометрии пользуются кинематическим способом образования поверхности путем непрерывного перемещения образующей линии в пространстве, причем производящая линия при своем движении может как сохранять свою форму, так и менять ее. [11]
Кроме самостоятельного значения, решение этой задачи может дать ответ на вопрос о полноте задания поверхности. В учебных целях решение такой задачи служит хорошим примером ознакомления с кинематическим способом образования поверхности . [12]
Источник
Что такое поверхность при задании кинематическим способом
Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б
Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.
Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.
В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.
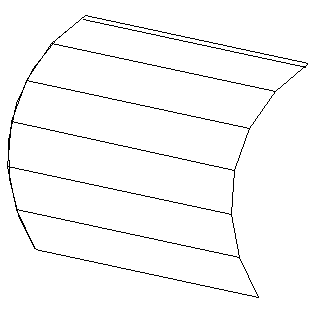
Рисунок 37
На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.
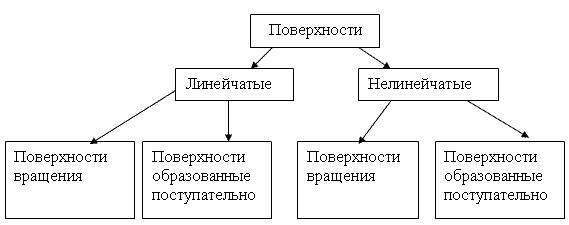
Рисунок 38
Линейчатые поверхности вращения – это конус, цилиндр.
Линейчатые поверхности поступательного движения – все гранные поверхности.
К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.
Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.
Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.

Рисунок 39
Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.
Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.

Рисунок 40
Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.
1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?
2. Назовите линейчатые поверхности вращения.
3. Какие нелинейчатые поверхности вы знаете?
4.Какая линия является направляющей у гранных поверхностей, какая является образующей?
5. Как образуется поверхность пирамиды, призмы?
6. Какая призма называется прямой?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник










