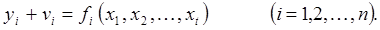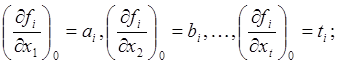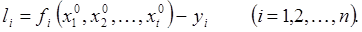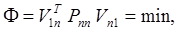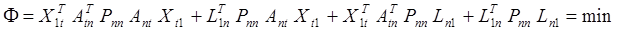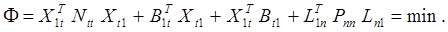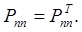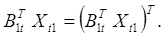Что такое параметрический способ уравнивания

Сущность параметрического способа уравнивания

При уравнивании геодезических сетей параметрическим способом первоначально выбираются так называемые параметры, через которые посредством уравнений связи выражается каждая измеренная величина. Поэтому непосредственно уравниваемыми величинами являются параметры, а затем уже по уравненным значениям параметров вычисляются уравненные значения непосредственно измеренных величин..

Пусть в геодезической сети измерено величин , , …, , из которых величин являются избыточно измеренными. Далее выбирается ряд независимых неизвестных параметров , , …, , через которые могут быть выражены значения измеренных величин , ( ). Число таких параметров должно быть равно числу избыточно измеренных величин. Каждая избыточно измеренная величина в геодезической сети приводит к возникновению одного уравнения связи вида

, ( ) , (7.43)

где , ( ) – истинные значения измеренных величин;

, ( ) – истинные значения параметров.

Уравнения (7.43) называются параметрическими уравнениями связи в общем виде .

Как уже ранее отмечалось, целью уравнительных вычислений является вычисление таких поправок в измеренные величины , при которых удовлетворялись бы все существующие зависимости между элементами сети, причем не только измеренными, но и вычисляемыми. Это означает, что если в левой части выражений (7.43) поставить уравненные значения измеренных величин, то должны измениться и правые части, а именно, должны измениться значения параметров , т.е. в правой части должны стоять соответствующие уравненные значения параметров.

(7.44)

уравненные значения измеренных величин, а через

(7.45)

уравненные значения параметров, где – приближенные значения неизвестных параметров , а – поправки к приближенным значениям параметров. Тогда система уравнений (7.43) может быть переписана в виде

, ( ) , (7.46)

, (7.44)

1. Гудков В.М., Хлебников А.В. Математическая обработка маркшейдерско-геодезических измерений. Учеб. для вузов. – М.: Недра, 1990.– 335 с.

2. Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений. – М.: Недра, 1977. 387 с.

3. Смолич Б.А. Уравнительные вычисления. Учеб. для техникумов – М.: Недра, 1989. – 245 с.

4. Мазмишвили А.И. Теория ошибок и метод наименьших квадратов. – М.: Недра, 1978. 311 с.

5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.1 – М.: Недра, 1970. 456с.

6. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.2 – М.: Недра, 1970. 576с.

7. Бермант А.Ф. Курс математического анализа. Часть 1. – М.: Госуд. изд-во физ-мат. литературы. 1959, 466 с.

8. Селиханович В.Г. Геодезия. Учеб. для вузов.Ч. II – М.: Недра, 1981. 544 с.

Источник

Уравнивание нивелирных сетей (Глава 2 дипломного проекта)

Страницы работы

Содержание работы

2. УРАВНИВАНИЕ НИВЕЛИРНЫХ СЕТЕЙ

2.1. Параметрический способ

Будем уравнивать нивелирную сеть по методу наименьших квадратов (МНК). Если результаты измерений неравноточны и известны их веса р_i, то принцип наименьших квадратов имеет вид

(17)

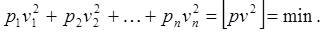
Введем вектор поправок к измеренным величинам и диагональную матрицу весов результатов измерений

(18)

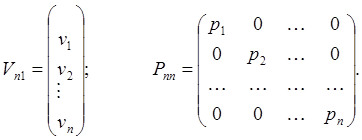
Тогда выражение (17) примет вид

(19)

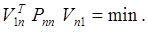
Существует два основных способа уравнивания – параметрический и коррелатный способы. Главная разница между этими способами заключается в различии типов исходных уравнений, решаемых на основе принципа наименьших квадратов.

Параметрический способ уравнивания заключается в том, что уравненные значения измеренных величин получаются из решения по методу наименьших квадратов уравнений, связывающих уравненные величины с системой функционально независимых аргументов, именуемых параметрами.

Рассмотрим порядок уравнивания параметрическим способом. Пусть независимо измерены n величин и при этом получены результаты y₁, y₂, … , y_n с весами p₁, p₂, … , p_n, соответственно. Надо произвести параметрическое уравнивание результатов измерений, в итоге которого должны быть получены значения независимых параметров x₁, x₂, … , x_tи уравненные значения измеренных величин y₁, y₂, …, y_n.

(20)

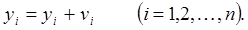
Здесь v_i– поправки к результатам измерений.

Выбирают независимые параметры ,количество которых должно быть равно числу необходимых измерений t:

Представляют каждое уравненное значение измеренной величины как функцию искомых параметров

с весом (21)

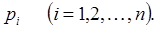
Выражения (21) называют параметрическими уравнениями связи. Искомые величины в них являются параметры x. Важную роль играет выбор независимых параметров. При выборе нужно учитывать, чтобы функции параметров уравнений были по возможности более простыми.

В ряде случаев эти уравнения имеют нелинейный вид относительно искомых параметров x_j, что затрудняет их непосредственное решение по методу наименьших квадратов. В связи с этим, уравнения (21) приводят к линейному виду, что называется линеаризацией. Для выполнения линеаризации вводят приближенные значения параметров – 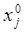. Тогда окончательные их значения будут равны

(22)

Здесь dx_j — поправки, определяемые из уравнивания.

Подставляя в (21) вместо x_j их значения из (22) получаем выражения

(23)

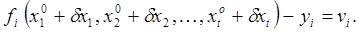
Полагая, что поправки dx_j достаточно малы, по сравнению с x_j, разлагаем эти выражения в ряд Тейлора и ограничиваемся членами первого порядка малости

(24)

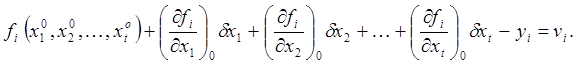
Частные производные здесь вычисляются при значениях аргументов .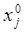

Тогда выражения (24) примут вид

(26)

Это параметрические уравнения связи, представленные в линейном виде, которые называются параметрическими уравнениями поправок. Коэффициентами этих уравнений являются частные производные функций по соответствующим параметрам. Свободными членами этих уравнений являются разности между функциями приближенных значений параметров и результатами измерений.

Введем матрицу коэффициентов параметрических уравнений поправок Аnt, вектор свободных членов Ln1 и вектор неизвестных Хt1

(27)

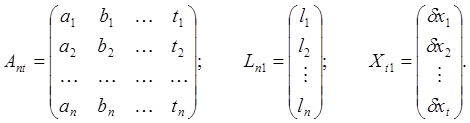
Принимая во внимание эти обозначения, а также обозначения (18) , представляем систему параметрических уравнений поправок (26) в виде матричного уравнения

(28)

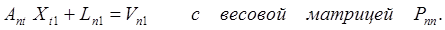
Решение матричного уравнения (28) подчиним условию наименьших квадратов

которое, в соответствии с (28), представим так

. (29)

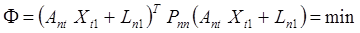
и введем обозначения

(30)

(31)

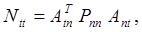
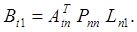
Тогда выражение (29) примет вид

Здесь учтено, что

Выражение 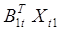представляет собой скаляр, а потому

Принимая это во внимание, можем написать окончательно

(32)

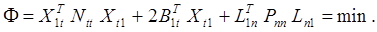
Транспонируя левую в правую части равенства (30), убеждаемся, что

(33)

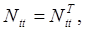
то есть матрица Ntt симметричная.

Для определения вектора Xt1, удовлетворяющего условию наименьших квадратов, произведем дифференцирование выражения (32) по этому вектору и приравняем полученный результат нулевому вектору.

Пользуясь правилами дифференцирования по вектору, получаем

или, после транспонирования и деления на 2,

Источник