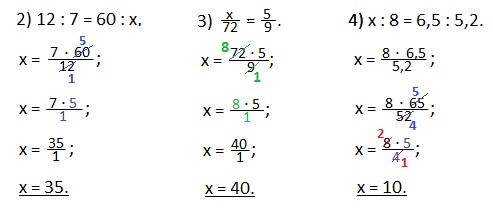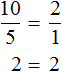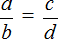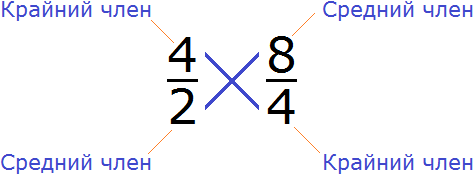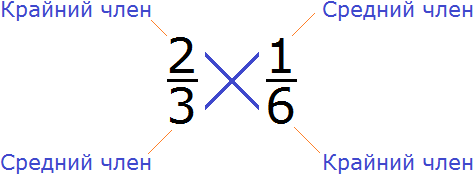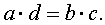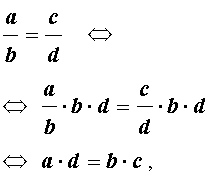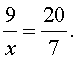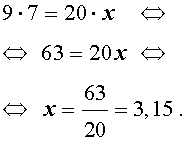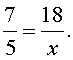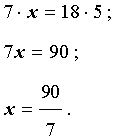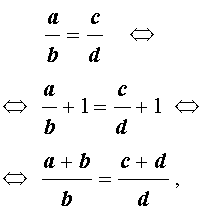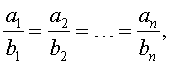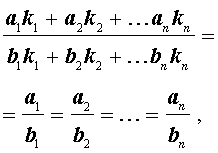6.1.1. Пропорция. Основное свойство пропорции
Равенство двух отношений называют пропорцией.
Тема: «Отношение» рассмотрена на предыдущем занятии («6.1. Отношение»).
a : b = c : d . Это пропорция. Читают: а так относится к b , как c относится к d . Числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Пример пропорции: 1 2 : 3 = 16 : 4 . Это равенство двух отношений: 12:3= 4 и 16:4= 4 . Читают: двенадцать так относится к трем , как шестнадцать относится к четырем . Здесь 12 и 4 -крайние члены пропорции, а 3 и 16 — средние члены пропорции.
Основное свойство пропорции.
Произведение крайних членов пропорции равно произведению ее средних членов.
Для пропорции a : b = c : d или a / b = c / d основное свойство записывается так: a·d = b·c .
Для нашей пропорции 12 : 3 = 16 : 4 основное свойство запишется так: 12·4 = 3·16 . Получается верное равенство: 48=48 .
Чтобы найти неизвестный крайний член пропорции, нужно произведение средних членов пропорции разделить на известный крайний член.
Примеры. Найти неизвестный крайний член пропорции.
1) х : 20 = 2 : 5. У нас х и 5 — крайние члены пропорции, а 20 и 2 — средние.
Решение.
х = (20·2):5 — нужно перемножить средние члены (20 и 2) и результат разделить на известный крайний член (число 5);
х = 40 : 5 — произведение средних членов (40) разделим на известный крайний член (5);
х = 8. Получили искомый крайний член пропорции.
Удобнее записывать нахождение неизвестного члена пропорции с помощью обыкновенной дроби. Вот как тогда запишется рассмотренный нами пример:
Искомый крайний член пропорции (х) будет равен произведению средних членов (20 и 2), деленному на известный крайний член (5).
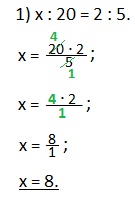
Сокращаем дробь на 5 (делим на 5 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного крайнего члена пропорции.
Чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов пропорции разделить на известный средний член.
Примеры. Найти неизвестный средний член пропорции.
5) 9 : х = 3 : 14. Число 3 — известный средний член данной пропорции, числа 9 и 14 — крайние члены пропорции.
Решение.
х = (9·14):3 — перемножим крайние члены пропорции и результат разделим на известный средний член пропорции;
х= 136:3;
х=42.
Решение этого примера можно записать иначе:
Искомый средний член пропорции (х) будет равен произведению крайних членов (9 и 14), деленному на известный средний член (3).
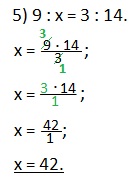
Сокращаем дробь на 3 (делим на 3 и числитель и знаменатель дроби). Находим значение х.
Если забыли, как сокращать обыкновенные дроби, то повторите тему: «5.4.2. Примеры сокращения обыкновенных дробей»
Еще такие примеры на нахождение неизвестного среднего члена пропорции.
Источник
Пропорция
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение 
равно отношению 
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции 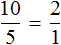выполнить деление в обеих дробях, то получится число 2 в обеих частях:
Предположим, что в классе 10 девочек и 5 мальчиков
Запишем отношение десяти девочек к пяти мальчикам:
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки
Теперь рассмотрим другой класс в котором две девочки и один мальчик
Запишем отношение двух девочек к одному мальчику:
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:
Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному» .
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам
а также отношение 12 девочек к 2 мальчикам
Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что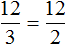 
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение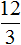 
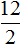
не пропорционально отношению 
.
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция 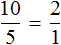состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2 . Понятно, что 2 равно 2.
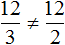
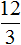
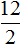
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
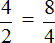
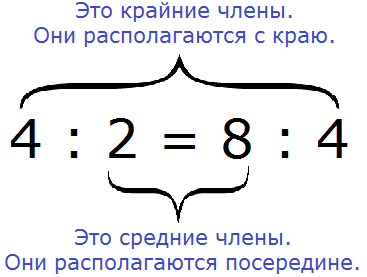
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция 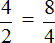. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция 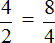составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция 
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция 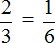составлена неправильно.
Поэтому в пропорции 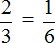разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Источник
Пропорции, члены пропорции, основное свойство пропорции
Содержание
 Пропорции, члены пропорции. Основное свойство пропорции |
| Производные пропорции |
| Свойства равных отношений |
Пропорции, члены пропорции. Основное свойство пропорции
Частное от деления числа a на число b называют отношением числа a к числу b .
Число a называют предыдущим членом отношения, число b – последующим членом отношения.
Пропорцией называют равенство двух отношений:
.
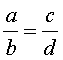
Иногда пропорцию записывают так:
И в одной, и во второй формах записи пропорции числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:
Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.
Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение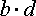 
.
В результате получим:
что и требовалось доказать.
Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.
ПРИМЕР 1 . Найти неизвестный член пропорции x , если
РЕШЕНИЕ . Воспользовавшись основным свойством пропорции, получаем:
ПРИМЕР 2 . Найти неизвестный член пропорции x , если
РЕШЕНИЕ . Воспользовавшись основным свойством пропорции, получаем:
ОТВЕТ :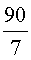 
.
Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если
.
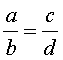
Производные пропорции
Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если
,
|  , |
|  , |
|  , |
|  , |
|  , |
|  |
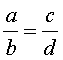
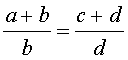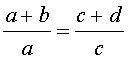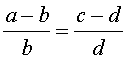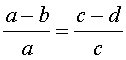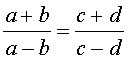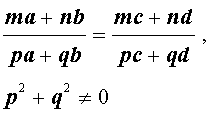В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично). Для этого к обеим частям пропорции
.
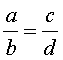
достаточно прибавить 1. В результате получаем,
что и требовалось.
ЗАМЕЧАНИЕ . Последнее из свойств пропорций является наиболее общим и может быть доказано, например, с помощью основного свойства пропорции.
Свойства равных отношений
Если выполнено соотношение
то выполнено и соотношение
– произвольные числа, которые не могут все одновременно равняться нулю.
Источник
