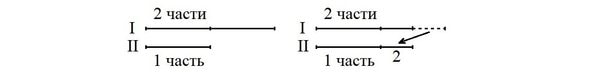Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.
В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.
Ответ: 18 детей в классе.
Составим вторую задачу.
В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?
Ответ: 8 мальчиков в классе.
Составим третью задачу.
В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
30, 20, ясных, пасмурных, июне
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
Источник
Статья «Применение метода обратных задач»
Эффективность применения метода обратных задач.
Кузьмина Татьяна Константиновна,
учитель начальных классов высшей квалификационной категории МБОУ «Гимназия 3 Зеленодольского муниципального района Республики Татарстан», г Зеленодольск.
E — mail автора: tatiana .874@ yandex . ru
С первого класса ребенка учат решать текстовые задачи. Решение простых задач не вызывает затруднения. Сложности возникают при решении составных задач, и из года в год эти дети испытывают всё большие затруднения. И главной причиной этих трудностей является несформированность умения анализировать текст задачи, правильно выделять известное и неизвестное, устанавливать взаимосвязи между ними, что является основой выбора действия для решения текстовой задачи.
При изучении сложных задач в курсе математики оказывается высоко эффективным применение метода обратных задач.
Путь преобразования прямой задачи в обратные задачи заставляет поднимать из сферы подсознания разнообразие связей, которые заключены в содержании задачи. Что обеспечивает глубокое и прочное усвоение материала, успех обучения решению задач.
Составление и решение обратной задачи представляет собой проверку решения прямой задачи. Во время преобразования учащийся практически познает связи между действиями. Суждения и умозаключения, использованные при решении прямой задачи, учащийся перестраивает при составлении и решении обратной задачи, при этом преодолевая инертность в мышлении. Составляя обратные задачи, учащиеся знакомятся со значительно большим разнообразием задач, чем в традиционных учебниках.
Для развития мышления ценный познавательный элемент заключается в процессе преобразования одной задачи в другую, в сравнении условий, решений, ответов задач.
Важно, чтоб дети понимали, что количество действий при решении прямой и обратной задач совпадает, количество комбинаций при составлении обратной задачи равно количеству данных в задаче, каждому действию прямой задачи соответствует действие той же ступени в обратной задаче.
Можно утверждать, что применение метода обратных задач — это способ развития творчества, разносторонности, мотивации к учению у школьников.
Урок математики в 4 классе.
Тема урока: составление и решение задач, обратных данной.
— создать условия для формирования навыка составления обратных задач по отношению к заданным; составлять задачи по схемам и строить схемы к задачам;
— способствовать развитию умений решать составные задачи, составлять задачи, обратные данной;
— применять способы устных и письменных приемов умножения и деления в вычислениях;
— способствовать развитию логического мышления (умения анализировать, сопоставлять, сравнивать), умения выделять главное, существенное при работе с задачами через стратегии критического мышления;
— способствовать развитию умение грамотно, логично, полно давать ответы на вопросы, осознанно подходить к собственному обучению.
Предметные: научатся решать составные задачи, составлять задачи, обратные данной, применять способы устных и письменных приемов умножения и деления в вычислениях, соблюдать порядок выполнения действий в выражениях со скобками.
Личностные: проявляют интерес, переходящий в потребность к расширению знаний, предложенных в учебнике или учителем.
Тип урока: комплексное применение знаний и способов действий
Формы работы : Групповая, парная, индивидуальная
— Предлагаю начать урок с высказывания математика:
«Геометрия полна приключений,
потому что за каждой задачей
скрывается приключение мысли.
Решить задачу –
это значит пережить приключение»
— Согласны вы с таким мнением, объясните.
2) Постановка темы. Мотивация.
— Предположите тему урока.
— Почему мы уделяем особое внимание на уроке математики решению задач?
— Отправляем мысли в приключения!
-Решите данные задачи:
А) С поля вывозили овощи на 11 машинах. Каждая из этих машин сделала по 9 рейсов и вывозила по з тонны овощей за рейс.
Б) У продавца было 20 сеток картофеля по 15 кг в каждой и 84 кг моркови в 7 сетках по 12 кг в каждой. За день продали 224 кг овощей. Сколько овощей осталось у продавца?
(Содержатся лишние данные.
Варианты решения: а)15х20+12х7+224 б)20х15+7х12-224 в)15х20+12х7-224 )
В) На завод отправлено 40 вагонов по 60 т угля в каждом и ряд вагонов по 90 т угля в каждом. Сколько всего тонн угля отправлено на завод?
(Недостаточно данных для решения задачи.
Варианты решения: а)60х40+90х20 б)(60+90)х40 в)40х60+20х90)
— Объясните выбор решения.
— На что нацелило вас данное задание?
(Быть внимательным при чтении текста задачи, чтобы правильно установить связь между данными, между данными и неизвестным.)
4) Работа по теме урока.
а)- Рассмотрим задачу в учебнике. Оцените формулировку задачи.
Стр.130 №252 (Аргинская И.И. 4 класс)
— Чем интересен вопрос задачи?
(Ответ не будет выражен числом)
— Какой вид краткой записи подойдёт для более точного понимания этой задачи?
— Решите задачу выражением.
Самостоятельное решение задачи.
— Сверьте ваши решения
б) — Сколько обратных задач можно составить?
Обратная задача: два шофера вывозили с поля картофель. Первая машина совершила 9 поездок и перевозила за 1 рейс 1500 кг, а вторая совершила 8 поездок и за каждый рейс перевозила в 2 раза больше первой. Сколько картофеля должны вывезти с поля 2 машины, если осталось ещё вывезти 6000кг?
— Решите задачу. в) Самостоятельная работа.
Работа в паре (карточки).
— Выберите обратные задачи, первую и вторую задачу решаете по вариантам. Затем сопоставьте свои ответы.
-1- На рынке продавали картофель в сетках. К концу дня осталось 120 сеток с картофелем, это в 6 раз меньше, чем было продано. Сколько килограммов картофеля было продано, если в каждой сетке по 50 кг картофеля?
-2- На рынке продавали картофель в сетках и в ящиках. Было 20 сеток и 15 ящиков, в ящиках картофеля было на 250 кг меньше, чем в сетках. Сколько картофеля было в сетках, если известно, что в ящик и в сетку помещается одинаковое количество картофеля?
-3- На рынке продавали картофель в сетках. К концу дня осталось 6000 кг картофеля, это в 6 раз меньше, чем было продано. Сколько сеток с картофелем было продано, если в каждой сетке по 50 кг картофеля?
— Сопоставьте ответы, проанализируйте решения в паре.
Чему научились? Какой вывод можем сделать по уроку?
Источник
Обратный ход
В 5 классе учащиеся должны освоить решение задач обратным ходом, то есть с конца. Этот приём позволяет закрепить взаимосвязь операций, его часто используют при решении составных задач, для решения которых надо использовать и другие способы. Начнём с подготовительной задачи.
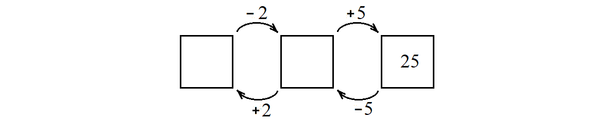
Задача 1. В автобусе едут 25 пассажиров. На первой остановке вышли два, вошли пять пассажиров. Сколько пассажиров едет в автобусе после первой остановки?
Решение. Выполним схематический рисунок, подсказывающий порядок вычислений.
Ответ. 28 пассажиров.
Теперь решим задачу, в которой нужно применить обратный ход, то есть провести вычисления в обратном порядке, применив обратные операции.
Задача 2. В автобусе едут несколько пассажиров. На первой остановке вышли два, вошли пять пассажиров. Сколько пассажиров ехало в автобусе до первой остановки?
Решение. Выполним схематический рисунок. После того, как вошли 5 пассажиров, их стало 25, значит, до этого их было 25 — 5 = 20. Дальше заполняем пустые клетки.
Ответ. 22 пассажира.
Задача 3. На двух полках стояло 30 книг. Когда с первой полки на вторую переставили 4 книги, то книг стало поровну. Сколько книг стояло на каждой полке первоначально?
Решение. Начнём с конца.
1) 30: 2 = 15 (книг) — стало на каждой полке после перестановки 4-х книг.
Вернём 4 книги на первую полку.
2) 15 + 4 = 19 (книг) — было на первой полке первоначально,
3) 15 — 4 = 11 (книг) — было на второй полке первоначально.
Ответ. 19 и 11 книг.
Замечание. Чтобы уравнять количество книг, с первой полки на вторую переставили половину разности, т. е. (19 — 11): 2 = 4 книги.
Рассмотрим задачу из ВПР для 5 класса.
Задача 4. На двух полках стояли книги — на первой полке в два раза больше, чем на второй. Когда с первой полки на вторую переставили две книги, то книг на полках стало поровну. Сколько книг стояло на каждой полке первоначально?
Решение. Пусть число книг на второй полке составляет 1 часть, а на первой — 2 части (рис. слева). Чтобы уравнять число книг, надо половину одной части переставить на вторую полку (рис. справа), т. е. две переставленные книги составляют половину одной части.
1) 2 * 2 = 4 (книги) — приходится на 1 часть, стояло книг на второй полке первоначально,
2) 4 * 2 = 8 (книг) — стояло на первой полке первоначально.
Ответ. 8 книг и 4 книги.
В заключение разберём решение задачи из казахстанского итогового экзамена «Математическая грамотность», аналога нашего ЕГЭ базового уровня. Преподаватель, обучавший казахстанских выпускников в Ютубе, дал неполное решение этой задачи при помощи уравнения. Приведём арифметическое решение этой задачи. Для начала тоже неполное.
Задача 5. В двух карманах было 150 монет. Затем семнадцать монет были перемещены из одного кармана в другой. В результате количество монет во втором кармане стало в 2 раза больше, чем в первом. Сколько монет было в первом кармане первоначально?
Решение. Определим, сколько монет стало в первом кармане после их перекладывания, для этого решим «задачу на части». Пусть новое числомонет в первом кармане составляет 1 часть, тогда во втором кармане — 2 части.
1) 1 + 2 = 3 (части) — приходится на 150 монет;
2) 150: 3 = 50 (монет) — стало в первом кармане;
3) 50 + 17 = 67 (монет) — было в первом кармане первоначально.
В чём же неполнота решения? Дело в том, что условие задачи «из одного кармана в другой» может означать как «из первого кармана во второй», так и «из второго кармана во первый». Второй случай приводит к ответу: 33 монеты.
Источник