- Метод простых итераций
- Материал из MachineLearning.
- Содержание
- Постановка задачи
- Метод простых итераций в общем виде
- Сходимость метода простых итераций
- Геометрическая интерпретация
- Метод релаксации
- Выбор параметра
- Ускорение сходимости
- Метод Вегстейна
- Программная реализация
- Примеры тестирования
- Итерационные методы решения СЛАУ
- Сущность итерационных методов решения систем линейных уравнений
- Метод Якоби (метод простых итераций СЛАУ)
- Готовые работы на аналогичную тему
- Метод Гаусса-Зейделя
- Итерационные методы решения системы линейных алгебраических уравнений
- Общие сведения об итерационных методах или методе простой итерации
- Метод Якоби
- Метод Зейделя
- Метод простой итерации
Метод простых итераций
Материал из MachineLearning.
Содержание
Постановка задачи
Пусть есть функция .
Требуется найти корень этой функции: такой при котором
Решение необходимо найти численно, то есть для реализации на ЭВМ. Для решения этой задачи предлагается использовать метод простых итераций.
Метод простых итераций в общем виде
Заменим исходное уравнение на эквивалентное ,и будем строить итерации по правилу . Таким образом метод простой итерации — это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение . Выясним условия сходимости метода и выбор начального приближения.
Сходимость метода простых итераций
Метод сходится, если при последовательность < >имеет предел.
Обозначим окресность точки радиуса , то есть .
Теорема 1. Если липшиц-непрерывна с константой на , то есть выполняется
при этом если также выполнено
, то уравнение имеет единственное решение на и метод простой итерации сходится к решению при любом выборе начального приближения .Так же справедлива оценка: ,
где — точное решение.
Из оценки видно, что метод линеен. Пусть непрерывно дифференцируема на , тогда из теоремы вытекают следующие утверждения:
Следствие 1. Если для , выполнено , и , тогда уравнение имеет единственное решение на и метод простой итерации сходится к решению.
Следствие 2. Если уравнение имеет решение , непрерывно дифференцируема на и . Тогда существует 0″ alt= «\eps > 0»/> такое, что на
уравнение не имеет других решений и метод простой итерации сходится к решению при
Геометрическая интерпретация
Рассмотрим график функции . Это озночает, что решение уравнения и — это точка пересечения с прямой :
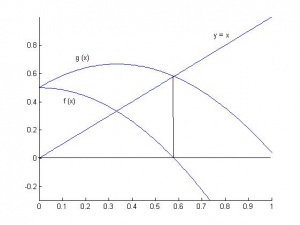
И следующая итерация — это координата пересечения горизонтальной прямой точки с прямой .
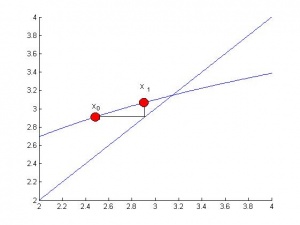
Из рисунка наглядно видно требование сходимости . Чем ближе производная к , тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если , то каждое следующее приближение строится с другой стороны от корня:
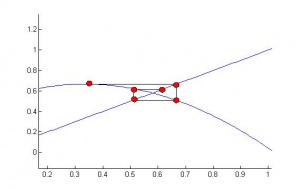
Метод релаксации
Где не меняет знака на отрезке, на котором ищется корень функции.
Положим и рассмотрим метод в этом случае.
Тогда получим метод ‘релаксации’:
для которого , и метод сходится при условии
Пусть в некоторой окресности корня выполняются условия
Тогда метод релаксации сходится при
Выбор параметра
Оценим погрешность метода релаксации
Применяя теорему о среднем получаем
Таким образом задача сводится к нахождению минимума функции
Из рассмотрения графика функции видно, что точка минимума определяется
Ускорение сходимости
Как следует из Теоремы 1, метод простых итераций линеен, то есть
Воспользуемся этим для оценки погрешности на каждой итерации. Запомним 3 последние итерации и выпишем их оценки:
Где нам известны (вычисленны по какому то линейному алгоритму),а найдем из системы. Получим:
Метод ускорения сходимости заключается в том, что после вычисления 3 приближений по линейно сходящемуся алгоритму, вычисляется новое приближение по уточняющему правилу (2).
Применительно к методу релаксации имеем:
Можно показать, что данный метод имеет уже квадратичную скорость сходимости.
Метод Вегстейна
Метод Вегстейна, вообще говоря, является модификацией метода секущих, однако его можно назвать и улучшенным методом простой итерации, преобразовав вычислительню формулу
Это двухшаговый метод, и для начала вычислений необходимо задать 2 приближения .
Программная реализация
Все методы были реализованы на языке C++. Доступ к методам осуществяется через класс
Примеры тестирования
Ошибкой будем считать и проверим скорость сходимости методов относительно друг друга.
Начальное приближение
1. Метод простой итерации с .
Сходимость за 28 шагов.
2. Метод простой итерации с .
Сходимость за 21 шаг.
3. Ускоренный метод простой итерации.
Сходимость за 3 шага.
4. Метод Вегстейна.
Сходимость за 3 шага.
Корень
Начальное приближение
1. Метод простой итерации с .
Сходимость за 23 шагов.
2. Метод простой итерации с .
Сходимость за 5 шаг.
3. Ускоренный метод простой итерации.
Сходимость за 4 шага.
4. Метод Вегстейна.
Сходимость за 4 шага.
Корень
Начальное приближение
1. Метод простой итерации с .
Сходимость за 43 шагов.
2. Метод простой итерации с .
Сходимость за 7 шагов.
3. Ускоренный метод простой итерации.
Сходимость за 5 шагов.
4. Метод Вегстейна.
Сходимость за 7 шагов.
Исходный код можно скачать Код программы
Источник
Итерационные методы решения СЛАУ
Вы будете перенаправлены на Автор24
Для решения систем линейных уравнений используется два основных метода решений, прямые методы, также называемые точными и итерационные методы, при использовании которых ответ в любом случае будет приближённым.
Особенность прямых методов состоит в том, что вычисления в них всегда проводятся точно, например, с использованием целых чисел, но при этом эти методы трудно применимы для вычисления решений для больших систем. К прямому методу относится, например, метод Крамера.
Ниже подробно рассмотрены итерационные методы решения СЛАУ.
Сущность итерационных методов решения систем линейных уравнений
Как уже отмечалось выше, итерационные методы в принципе являются приближёнными. Их сущность состоит в том, что сначала записывается некоторая последовательность столбцов матрицы, после чего производится поочередное вычисление каждого столбца. Каждый новый столбец вычисляется на основе вычисленных предыдущих, при этом с каждым вычислением получается всё более точное приближение искомого решения. Когда достигнута необходимая точность, процесс вычисления прерывают и в качестве решения используют последний вычисленный столбец.
Процесс вычисления одного столбца называется итерацией.
Различают несколько основных способов итерационного решения СЛАУ:
Метод Якоби (метод простых итераций СЛАУ)
Рассмотрим систему уравнений, с коэффициентами, которые можно записать в виде матрицы:
$A=\left(\begin
Саму же систему уравнений можно записать в виде равенства $A \cdot X = F$, где $X$ — вектор-столбец собственных значений системы, а $F$ — вектор-столбец свободных членов.
Метод состоит в том, чтобы в каждом уравнении системы выразить соответственно $x_1, x_2,…, x_n$ и затем получить новую матрицу $B$, у которой элементы главной диагонали принимают нулевые значения.
В общем виде формула для вычисления корней уравнений записывается так: $\overrightarrow
Добиться такого вида от системы можно следующими способами:
Готовые работы на аналогичную тему
$B= E – D^<-1>A=D^<-1>(D-A), \overrightarrow
Здесь $D$ — матрица, у которой нулевые все элементы, кроме элементов на главной диагонали, а на главной диагонали находятся соответствующие элементы матрицы $A$. Матрицы $U$ и $L$ означают верхнетреугольную матрицу и нижнетреугольную соответственно; их значимые элементы соответствуют частям матрицы $A$. Буквой $Е$ же обозначается единичная матрица соответствующей размерности.
Процедура нахождения корней тогда запишется так:
$\overrightarrow
Для конкретного элемента она будет выглядеть так:
$x_^
буквой $(k)$ во всех формулах выше обозначается номер итерации, сама же формула $(1)$ называется рекуррентной.
Окончание вычисления происходит в том случае, если разница между вычислениями в двух соседних итераций составляет не более чем $ε_1$:
В упрощённой форме условие окончания итераций выглядит как $||x^<(n+1)>-x^<(n)>||$
Порядок решения СЛАУ методом Якоби такой:
- Приведение системы уравнений к виду, в котором на каждой строчке выражено какое-либо неизвестное значение системы.
- Произвольный выбор нулевого решения, в качестве него можно взять вектор-столбец свободных членов.
- Производим подстановку произвольного нулевого решения в систему уравнений, полученную под пунктом 1.
- Осуществление дополнительных итераций, для каждой из которых используется решение, полученное на предыдущем этапе.
Метод Гаусса-Зейделя
Сущность этого метода состоит в том, что в нём переносятся в правые части все члены уравнений, индекс при которых больше индекса, выражаемого $x$. В краткой форме это можно записать так:
$(L + D) \cdot \overrightarrow
Сами итерации в методе Гаусса-Зейделя производятся по формуле:
$(L +D)\overrightarrow
Метод Гаусса-Зейделя похож на метод Якоби, но здесь полученные значения переменных используются не исключительно для следующей итерации, а сразу для следующего вычисления значения $x$.
Метод простых итераций: пример решения
Дана система уравнений:
$\begin
Решите данную систему с помощью метода простых итераций.
Выберем в качестве нулевого приближения корни $(0; 0; 0; 0)$ и подставим их в преобразованную систему:
$\begin
Проведём 5 итераций, используя на каждой результат, полученный с предыдущей и для них получим следующую таблицу:
Рисунок 1. Таблица итераций для решения СЛАУ. Автор24 — интернет-биржа студенческих работ
Продолжать вычисление можно до достижения заданной требуемой точности. Точный ответ системы — $(1; 2; -1; 1)$.
Источник
Итерационные методы решения системы линейных алгебраических уравнений
В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
Общие сведения об итерационных методах или методе простой итерации
Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .
Рассмотрим систему A x = b .
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.
Метод Якоби
Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.
Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
b i j = — a i j / a i i , i , j = 1 , 2 . . . , n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
d i = b i / a i i , i = 1 , 2 , . . . , n
Расчетная формула метода простой итерации:
x ( n + 1 ) = B x ( x ) + d
Матричная запись (координатная):
x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b
Критерий окончания в методе Якоби:
x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε
В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:
x ( n + 1 ) — x ( n ) ε
Решить СЛАУ методом Якоби:
10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10
Необходимо решить систему с показателем точности ε = 10 — 3 .
Приводим СЛАУ к удобному виду для итерации:
x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1
Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01
Аналогичным способом вычисляются приближения к решению:
x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111
Находим норму матрицы В , для этого используем норму B ∞ .
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:
x ( n + 1 ) — x ( n ) ε
Далее вычисляем нормы разности векторов:
x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .
Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.
x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .
Метод Зейделя
Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.
x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +
+ . . . + b i m x m ( n ) + d i
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Решим 3 системы уравнений:
2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1
Приведем системы к удобному для итерации виду:
x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .
Отличительная особенность, условие сходимости выполнено только для первой системы:
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109
Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.
2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129
Итерационный процесс разошелся.
Решение: x 1 = 1 , x 2 = 2
3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2
Итерационный процесс зациклился.
Решение: x 1 = 1 , x 1 = 2
Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x = x — τ ( A x — b ) , τ — итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .
Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .
Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .
τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .
Источник




