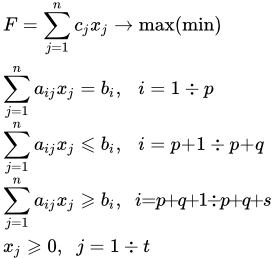Что такое графический способ решения задач линейного программирования

Решение задач линейного программирования графическим методом

Описание метода

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Теперь мы можем искать экстремум целевой функции
(1.1) .

Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .

Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.

Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .

Пример решения задачи линейного программирования графическим методом

Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.

Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)

Тогда экономико-математическая модель задачи имеет вид:

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).

Прямые и являются осями координат.

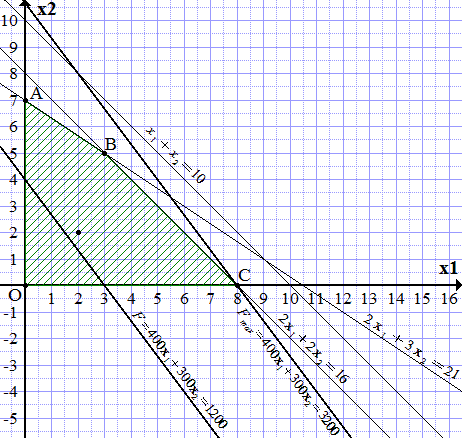
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

Решить задачу линейного программирования графическим методом.

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).

Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).

Строим прямую .
Строим прямую (ось абсцисс).

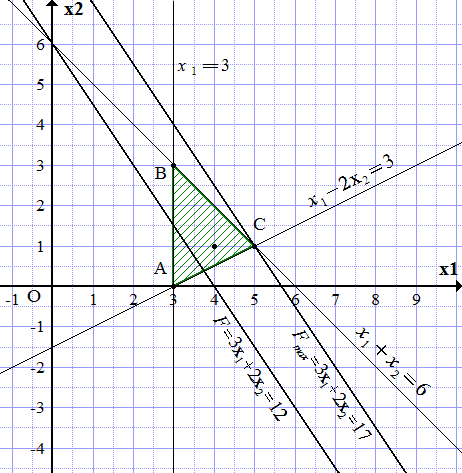
Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Пример отсутствия решения

Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Решаем задачу графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).

Прямые и являются осями координат.

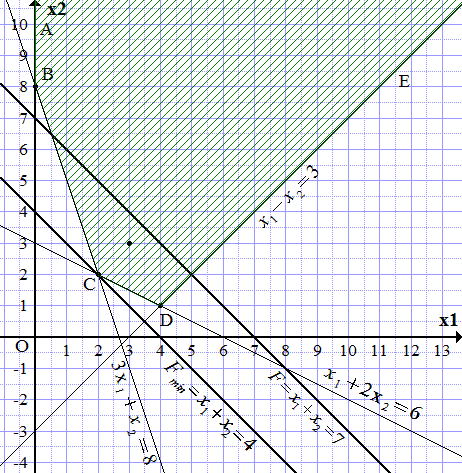
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .

Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.

Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:

Максимального значения не существует.
Минимальное значение
.

Автор: Олег Одинцов . Опубликовано: 08-08-2016

Источник

Основы линейного программирования

Задача линейного программирования

Общая задача линейного программирования формулируется следующим образом.
Найти максимум (или минимум) линейной функции n переменных :
(1.1)
при ограничениях вида
(1.2)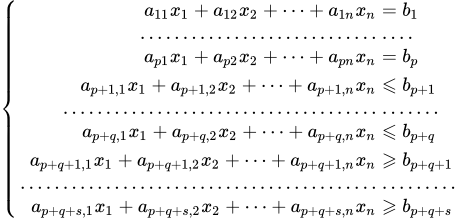
(1.3) .

Переменные задачи часто записывают в виде n-мерного вектора:
.

Линейная функция (1.1) называется целевой функцией. В задаче нужно найти такие значения переменных , которые удовлетворяют системе ограничений (1.2) – (1.3), и при которых целевая функция F имеет наибольшее (или наименьшее) значение.

Система ограничений (1.2) может состоять из равенств
,
и неравенств обоих знаков:
, или
.

В системе ограничений особо выделяют ограничения, связанные с не отрицательностью некоторых переменных (1.3), которые являются следствием физических свойств величин, описываемых этими переменными.

Допустимое решение (план) задачи линейного программирования – это такие значения переменных , которые удовлетворяют системе ограничений (1.2) и условиям не отрицательности (1.3). Допустимое решение также называют планом.
Область допустимых решений (ОДР) – это множество всех допустимых решений.
Оптимальное решение (оптимальный план) или просто решение задачи линейного программирования – это такое допустимое решение задачи, при котором целевая функция имеет экстремальное значение. Оптимальное решение также называют оптимальным планом.

Различные формы задач ЛП

Теорема
Любую общую задачу линейного программирования (1.1) – (1.3) можно привести к каноническому виду (1.4). А любую задачу в канонической форме можно привести к любой из задач в симметричной форме (1.5) или (1.6).

При таких преобразованиях переменные задач могут не совпадать. Могут вводиться новые переменные, а также переменные одной из задач могут линейно выражаться через переменные той же задачи, записанной в другой форме.

Дополнительная переменная (вспомогательная переменная) – это переменная, которая вводится для преобразования неравенства в равенство. Дополнительную переменную также называют вспомогательной переменной. Например, неравенство

переводится в равенство, введением дополнительной неотрицательной переменной :
.

Графический метод решения

Свойства решений задач линейного программирования (ЛП) наглядно демонстрирует графический метод решения.

Решение задачи линейного программирования графическим методом.

Графическим методом можно решить задачу, если она имеет две переменные, или ее можно привести к задаче с двумя переменными.

Решим графическим способом следующую задачу.
(2.1)
(2.2)
(2.3) .

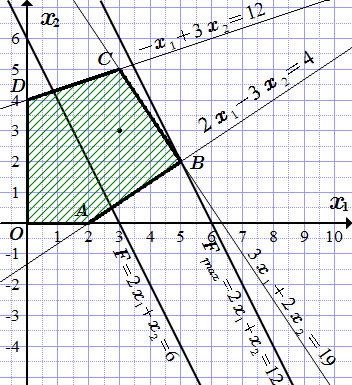
Сначала проводим оси системы координат, и построим область допустимых решений (ОДР), которая определяется системой неравенств (2.2) и условиями не отрицательности переменных (2.3). Для построения ОДР, строим прямые, проходящие через границы неравенств:
.
С одной стороны каждой из построенных прямых соответствующее неравенство выполняется, а с другой стороны – нет. Поэтому ОДР ограничена этими прямыми. Также ОДР может быть ограничена осями координат, в силу неравенств . Замечаем, что точка удовлетворяет всем неравенствам (2.2) и (2.3). Поэтому она принадлежит ОДР. Заштриховываем область по границам прямых и осям координат, чтобы в нее вошла точка . Получаем, что ОДР является множеством точек внутри многоугольника вместе с его границей.

Теперь рассмотрим целевую функцию (2.1). Построим ее линию уровня, приравняв F к любому значению, например :
(2.4) .
Строим прямую . С левой стороны от этой прямой . С правой стороны, . И чем больше мы удаляемся вправо и вверх, тем больше значение целевой функции F . Проводим прямую, параллельную прямой (2.4), так, чтобы она была максимально удалена в сторону увеличения значений F , то есть вправо, и при этом проходила хотя бы через одну точку ОДР. Такая прямая проходит через точку B с координатами . Это точка имеет наибольшее значение F среди всех точек ОДР. Поэтому является оптимальным планом с максимальным значением целевой функции:
.

Свойства решений задач ЛП

Графический метод иллюстрирует основные свойства решений задач ЛП. Мы увидели, что поскольку ОДР ограничена конечным числом прямых, то она является выпуклым многоугольником. Далее, целевая функция не может иметь экстремума во внутренней точке ОДР, а достигает экстремума только на границе. Причем экстремум достигается в одной из вершин многоугольника ОДР. Если взять целевую функцию , то экстремум будет на отрезке BC . То есть экстремум может достигаться в двух вершинах, и во всех точках отрезка между ними.

Эти свойства имеют место и в более общем случае, когда число переменных больше двух. Только вместо плоскостей будут гиперплоскости, а вместо многоугольников – многогранники. Так, если рассмотреть задачу ЛП в симметричной форме ⇑, то ОДР является выпуклым многогранником, ограниченным гиперплоскостями и . Целевая функция может достигать экстремум только на границе ОДР. При этом экстремум достигается обязательно на одной из вершин многогранника ОДР. Если экстремум достигается на нескольких вершинах, то оптимальными планами являются также все точки выпуклого многогранника, построенного на этих вершинах.

Далее приводим более строгую трактовку этих рассуждений.

Теорема о выпуклости ОДР
Область допустимых решений задачи линейного программирования является выпуклым множеством.

Теорема об оптимальном решении
Если задача линейного программирования имеет единственное решение, то оптимальный план является угловой точкой ОДР. Если существует несколько оптимальных планов, то в него входят две или более угловых точек, и любая выпуклая линейная комбинация этих угловых точек также является оптимальным планом. То есть задача имеет бесконечно много решений.

Выпуклое множество Возьмем две произвольные точки, принадлежащие некоторому множеству. Если все точки отрезка, соединяющего эти точки, принадлежат этому множеству, то такое множество называется выпуклым. Угловая (крайняя) точка выпуклого множества – это точка, через которую нельзя провести отрезок так, чтобы она была внутренней точкой отрезка, концы которого принадлежат множеству. Угловую точку также называют крайней точкой. Опорный план – это план (допустимое решение), который является угловой точкой (вершиной многогранника) области допустимых решений.

Поскольку в задачах линейного программирования система ограничений содержит конечное число неравенств, то ОДР является многогранником. Тогда угловые точки ОДР являются вершинами многогранника.

Лемма
Оптимальный план задачи линейного программирования является опорным планом, и может быть выбран из совокупности ее опорных планов.

Выпуклая линейная комбинация точек – это множество точек , векторы которых, относительно начала системы координат, определяются по формуле:
, где .

Для двух точек, выпуклая линейная комбинация и является отрезком с концами и . Для трех точек, если и не лежат на одной прямой, выпуклая линейная комбинация этих точек является треугольником с вершинами и . Если же эти точки лежат на одной прямой, то их выпуклая линейная комбинация является отрезком, концы которого совпадают с двумя из этих точек. При этом одна из точек будет внутренней точкой отрезка.

Теорема
Угловая точка ОДР (1.2) – (1.3) является решением системы из n уравнений, полученной из (1.2) – (1.3), вычеркиванием части неравенств, и заменой оставшихся неравенств равенствами.

Задачи линейного программирования в канонической форме

Рассмотрим задачу линейного программирования, записанную в канонической форме ⇑. В произвольном случае, не все строки матрицы коэффициентов , могут быть линейно независимыми. Пусть r – ранг матрицы коэффициентов, то есть число линейно независимых строк. Это означает, что линейными преобразованиями, систему уравнений (1.4) можно привести к эквивалентной системе, содержащей r линейно независимых строк.

Выше мы указали, что оптимальный план является угловой точкой ОДР. Но угловая точка получается из системы ограничений, заменой части неравенств равенствами, чтобы в результате получилась система из n линейно независимых уравнений. Решая эту систему, можно найти координаты угловой точки.

Для задачи в канонической форме это сводится к тому, что мы должны добавить к системе уравнений еще уравнений вида . Полученное решение такой системы уравнений является опорным планом.

Свободные переменные – это переменные задачи ЛП в канонической форме, на которые, в рассматриваемом опорном плане, наложено условие их равенства нулю: . Базисные переменные – это переменные задачи ЛП в канонической форме, которые в рассматриваемом опорном плане, не являются свободными. Они имеют неотрицательные значения, которые определяются из решения системы уравнений (1.4). Невырожденный план (невырожденное решение) – это опорный план, в котором все базисные переменные отличны от нуля. Вырожденный план (вырожденное решение) – это опорный план, в котором есть одна или несколько базисных переменных, равных нулю. Векторы условий – это n векторов, которые являются столбцами матрицы коэффициентов системы (1.4). Базис – это r векторов, которые являются столбцами матрицы коэффициентов системы (1.4) при базисных переменных. То есть базис – это векторы условий при базисных переменных.

Если в рассматриваемой угловой точке план не вырожден, то в ней имеется только один набор базисных переменных. Если же план вырожден, то в этой точке имеется два или более набора базисных переменных.

Теорема о числе базисных переменных
При решении задачи линейного программирования в канонической форме ⇑, в любом опорном плане имеется r базисных переменных ⇑. Отсюда следует, что в опорном плане как минимум переменных равны нулю. Здесь n – число переменных; r – ранг матрицы системы ограничений (1.4), из которой определяются значения базисных переменных.

Методы решения задач

Графический метод

Решение задачи графическим методом мы рассмотрели выше ⇑. Он применим, если в задаче имеются две переменные. Также он применим, если имеется n переменных и система ограничений содержит линейно независимых уравнения. Тогда, решая систему ограничений, мы можем выразить переменных через и , или через две другие переменные. В результате получим задачу с двумя переменными, которую можно решить графическим методом.

Метод перебора вершин

В этом методе мы используем тот факт, что оптимальный план является угловой точкой ОДР. А если задача имеет множество решений, то среди них имеются угловые точки.

В методе перебора вершин мы находим все угловые точки, и вычисляем в них значения целевой функции. Далее, из этих значений, определяем наибольшее или наименьшее значение целевой функции.

Решение задачи

Решим задачу (2.1) – (2.3) методом перебора вершин. При этом мы можем использовать результаты, полученные при решении графическим методом ⇑. Там мы нашли, что ОДЗ является многоугольником OABCD . И мы нашли координаты его вершин. Для каждой вершины мы можем вычислить значение целевой функции (2.1). Сравнивая их, можно определить наибольшее значение.

Но мы применим более общий метод, который работает при любом числе переменных, а не только для двух.

Для этого приведем задачу к канонической форме, вводя три дополнительные неотрицательные переменные :
(П.1)
(П.2)
(П.3) .

В этой задаче переменных. Система ограничений (П.2) содержит 3 линейно независимых уравнения. Поэтому в произвольной угловой точке имеется свободные переменные, и 3 базисные. Перебираем все возможные сочетания свободных переменных, приравниваем их к нулю, и, решая систему (П.2), определяем значения базисных переменных.

1) В качестве свободных переменных возьмем и . Приравниваем их к нулю, и подставляем в (П.2); получаем: . Поскольку все , то мы нашли угловую точку ОДР или, что тоже самое, вершину многогранника ОДР: . На построении ⇑ ей соответствует точка O .

2) Возьмем свободные переменные и . Подставляя их нулевые значения в (П.2), получаем систему:

Решаем ее: . Поскольку все , то это угловая точка: , На построении ⇑ ей соответствует точка D .

3) Возьмем свободные переменные и . Подставляем их нулевые значения в (П.2). Решая систему, получаем: . Поскольку , то эта точка не принадлежит ОДЗ. Поэтому она не может быть планом задачи. Отбрасываем ее. На рисунке ⇑ ей соответствует точка пересечения прямой AB с осью .

4) Свободные переменные . Подставляя их нулевые значения в (П.2), находим: . Здесь также есть отрицательная переменная . Эта точка также не принадлежит ОДЗ. Отбрасываем ее. Это точка пересечения прямой BC с осью .

5) Свободные переменные . Подставляя в (П.2), находим решение системы: . Поскольку , то и эта точка не принадлежит ОДЗ. Отбрасываем ее. Это точка пересечения прямой DC с осью .

6) . Решение системы: . Поскольку все , то мы нашли угловую точку, которой на построении ⇑ соответствует точка A .

7) . Решение системы: . , точка не принадлежит ОДЗ. На рисунке ей соответствует точка пересечения прямой BC с осью .

8) . Решение системы: . , точка не принадлежит ОДЗ. Это точка пересечения прямых AB и DC.

9) . Решение системы: . Все . Это угловая точка – точка C .

10) . Решение системы: . Все . Это угловая точка. На построении ⇑ ей соответствует точка B .

Итак, мы нашли все угловые точки ОДР. Находим в них значения целевой функции.
;
;
;
;
.

Наибольшим является значение целевой функции в точке B . Решение задачи: .

Симплексный метод

Для решения задачи симплексным методом, сначала задачу приводят к канонической форме. Далее выбирают любой опорный план с некоторым набором базисных переменных. Потом определяют свободную переменную, которую нужно включить в базис, чтобы при такой замене произошло наибольшее увеличение целевой функции. Определяют переменную, выходящую из базиса и с помощью линейных преобразований, совершают переход к новым базисным переменным. В результате получают новый план, значение целевой функции которого ближе к экстремальному. Процесс повторяют до тех пор, пока целевая функция не достигнет экстремального значения.

В геометрической интерпретации это означает следующее.
1. Вначале мы выбираем любую вершину многогранника ОДР.
2. Добавляя в базис новую переменную, выбираем направление до смежной вершины вдоль ребра многогранника, двигаясь по которому целевая функция наиболее быстро возрастает.
3. Переходим на новую вершину по выбранному в пункте 2 направлению, исключая из базиса одну из переменных.
4. Повторяем пункты 2 и 3, пока не достигнем экстремума.

Решение задачи

Рассмотрим задачу (2.1) – (2.3). Как и при решении методом перебора вершин, вводим три дополнительных неотрицательных переменных . Получаем задачу в канонической форме:
(С.1)
(С.2)
(С.3) .
Решаем задачу симплексным методом.

1. Вначале нам нужно найти любой опорный план, удовлетворяющий системе ограничений (С.2) – (С.3). Самый простой способ – это взять в качестве базиса дополнительные переменные . При этом из системы (С.2) мы сразу можем выразить базисные переменные через свободные:
(С.4)
Приравнивая свободные переменные и к нулю, получаем первый опорный план, который мы обозначим буквой O : , или в сокращенной форме . Значение целевой функции: .
На рисунке ⇑, этому плану соответствует точка .

2. Теперь попробуем найти смежную вершину многогранника ОДР, в которой значение целевой функции было бы больше . Для этого нужно переместиться из вершины O вдоль одного из ребра многогранника на небольшое расстояние по направлению к смежной вершине и посмотреть, увеличилась ли при этом целевая функция?

2.1. Проверим, как изменится целевая функция, если свободной переменной вместо нулевого, присвоить положительное значение . При этом считаем, что мало отличается от нуля. То есть сделаем оценку свободной переменной . Положим, . Тогда, чтобы выполнялась система ограничений (С.4), необходимо также изменить базисные переменные:
.
Свободная переменная по прежнему равняется нулю. Подставляя в (С.4), и удаляя равные слагаемые в обеих частях равенств, получаем:
(С.5)
Обозначим эту новую точку как . Найдем разность значений целевой функции в точках и :

.
Таким образом, если переменной присвоить положительное значение , то целевая функция увеличится на .

2.2. Проделаем тоже самое с переменной . То есть сделаем оценку для свободной переменной . Положим, . Чтобы выполнялась система ограничений (С.4), также изменим базисные переменные. Положим . Свободная переменная при этом равняется нулю. Подставляя в (С.4), и удаляя равные слагаемые в обеих частях равенств, получаем:
(С.6)
Обозначим эту новую точку как . Найдем разность значений целевой функции в точках и :

.
Если переменной присвоить положительное значение , то целевая функция увеличится на .

2.3. Итак, мы нашли, что если переменной или присвоить положительное значение, то целевая функция увеличится. Это означает, что первый опорный план не оптимален. Целевую функцию можно увеличить введением в базис или . При увеличении на единицу, целевая функция увеличится на . При увеличении на единицу, целевая функция увеличится на . В первом случае увеличение больше. Поэтому вводим в базис переменную . То есть считаем, что она может принимать отличные от нуля положительные значения.

3. Теперь определим следующий опорный план, то есть новую вершину многогранника ОДР с более высоким значением F . Определяем переменную, выходящую из базиса. Для этого нужно присвоить переменной максимально большое положительное значение, но чтобы при этом удовлетворялась система ограничений (С.4). При этом одна из переменных обратится в нуль. Ее мы исключим из состава базисных переменных. Переменная по прежнему имеет нулевое значение. Подставим в (С.4) :

Далее будем увеличивать до тех пор, пока одна из переменных не обратиться в нуль. Если и дальше продолжить увеличение , то эта переменная станет отрицательной, что не допустимо.

Поскольку , то переменная всегда будет положительной. Переменная обращается в нуль при . Переменная – при . Минимальное из этих величин . При этом значении, . Если положить , то переменная станет отрицательной, что не допустимо.

Выводим , и вводим в состав базисных переменных. Для этого над системой (С.4) выполняем линейные преобразования, чтобы выразить базисные переменные через свободные . В результате линейных преобразований получаем эквивалентную систему:
(С.7)
Приравнивая свободные переменные к нулю, получаем второй опорный план. Обозначим его буквой A : . Значение целевой функции:
.
На рисунке ⇑, этому плану соответствует точка . То есть в результате мы перешли из вершины в вершину многогранника ОДР.

4. Повторяем шаги 2 и 3.

4.1. Попробуем ввести в базис. Положим . Подставляем в (С.7):

Изменение целевой функции:
.

4.2. Попробуем ввести в базис . Положим . Подставляем в (С.7):

Изменение целевой функции:
.

Итак, если ввести в базис , то целевая функция увеличится. А если – уменьшится. Поэтому вводим в базис .

5. Определяем переменную, выходящую из базиса. Для этого присвоим переменной максимально большое положительное значение, но чтобы при этом удовлетворялась система ограничений (С.7). Переменная по прежнему сохраняет нулевое значение. Подставим в (С.7) :

Переменная положительна при любых значениях . Переменная обращается в нуль при ; переменная – при . Наименьшее: . При этом переменная принимает нулевое значение и выходит из базиса.

Выводим из базиса. Для этого выражаем базисные переменные через свободные , преобразовав систему (С.7):
(С.8)
Приравнивая свободные переменные и , получаем третий опорный план, который обозначим буквой B : . Значение целевой функции:
.
На рисунке ⇑, этому плану соответствует точка .

6. Повторяем шаги 4 и 5.

6.1. Попробуем ввести в базис . Положим . Подставляем в (С.8):

Изменение целевой функции:

.
. Введение в базис не приведет к увеличению значения целевой функции.

6.2. Попробуем ввести в базис . Положим . Подставляем в (С.8):

Изменение целевой функции:

.
И здесь . Введение в базис также не приведет к увеличению значения целевой функции. Поэтому последний план B оптимален.

Транспортная задача

Транспортную задачу можно решить симплексным методом. Однако имеются методы, которые позволяют получить решение другими, как правило, более легкими способами, используя специфичный вид системы ограничений (Т.2) – (Т.3). Одним из таких методов является метод потенциалов. В нем, как и в симплексном методе ⇑, используется метод последовательного улучшения плана. Мы кратко рассмотрим применение этого метода на примере решения простой транспортной задачи.

Решение транспортной задачи методом потенциалов

Пусть у нас имеется поставщика с мощностями , и потребителя с мощностями . Стоимость перевозки единицы груза от -го поставщика к -му потребителю задана в таблице:
(Т.5)
Требуется найти план перевозок, при котором суммарные затраты на перевозки минимальны.

Вначале нужно подсчитать суммы мощностей поставщиков и потребителей. Если сумма мощностей поставщиков равна сумме мощностей потребителей, то такая задача называется задачей с правильным балансом, или задачей с закрытой моделью. Задача, в которой суммы мощностей поставщиков и потребителей не совпадают, называется задачей с неправильным балансом, или задачей с открытой моделью. Если у задачи открытая модель, то ее сначала нужно привести к закрытой модели, добавлением фиктивного поставщика или потребителя с нулевыми стоимостями перевозок. В нашем случае, сумма мощностей поставщиков равна сумме мощностей потребителей:
.
Модель закрытая, задачу можно решать методом потенциалов.

Задача имеет неотрицательных переменных:
.

Задача (Т.1) – (Т.4) имеет канонический вид. Подсчитаем число базисных переменных. Система ограничений (Т.2) – (Т.3) содержит уравнений:
(Т.6)
Существует теорема, согласно которой, ранг r системы ограничений транспортной задачи равен . То есть система (Т.6) имеет линейно независимых уравнения. Тогда по теореме о числе базисных переменных ⇑, угловая точка ОДР имеет r = 4 базисных переменных, и свободных.

Поясним, почему ранг системы равен . Это означает, что эти уравнения имеют одну линейную зависимость. Найдем ее. Поскольку модель закрытая, то . Подставим (Т.2) и (Т.3):
;
.
Отсюда видно, что если сложить первые два уравнения (Т.6), и вычесть последние три, то получим тождество . Что означает, что система (Т.6) имеет линейную зависимость.

Применяем метод последовательного улучшения плана.

Метод северо-западного угла

1. Вначале нам нужно найти любой опорный план, удовлетворяющий системе ограничений (Т.6) и условию не отрицательности переменных. Существует несколько методов, позволяющих это сделать. Мы применим метод северо-западного угла.

Заносим исходные данные в таблицу и даем максимально возможную поставку в левую верхнюю клетку . В ней находится объем перевозки от 1-го поставщика к 1-му потребителю. В общем случае, максимально возможная поставка в клетку равна . В нашем случае, мощность первого поставщика равна мощности первого потребителя . Поэтому наибольшая поставка в клетку равна 5. Заносим 5 в клетку .

Теперь нам нужно вычеркнуть либо первую строку, либо первый столбец. В нашем случае, как первый поставщик, так и первый потребитель исчерпали свои мощности. Однако вычеркнуть мы можем только одну строку или один столбец. Вместе их вычеркнуть нельзя. Вычеркиваем по своему усмотрению первую строку.

Далее заполняем левую верхнюю клетку в оставшейся части таблицы, среди не зачеркнутых клеток. Это клетка . В ней находится объем перевозки от 2-го поставщика к 1-му потребителю. Нам нужно дать в нее максимально возможную поставку. Но потребности первого потребителя уже полностью удовлетворены первым поставщиком. Поэтому наибольшая поставка в клетку равна нулю. Заносим 0 в клетку . Здесь возник случай, когда переменная является базисной, но ее значение равно нулю.

Заполняем верхнюю левую ячейку предыдущей таблицы, и вычеркиваем первый столбец.

Далее нам нужно вычеркнуть либо строку, либо столбец, содержащий заполненную клетку . Поскольку потребности первого потребителя удовлетворены, то вычеркиваем первый столбец.

Снова заполняем левую верхнюю клетку в оставшейся части таблицы, среди не зачеркнутых клеток. Это клетка . Мощность второго потребителя равна 6, неизрасходованная мощность второго поставщика: 10. Минимальное из этих чисел: 6. Даем в клетку поставку 6, и вычеркиваем 2-го потребителя, поскольку его потребности удовлетворены.

Первый опорный план.

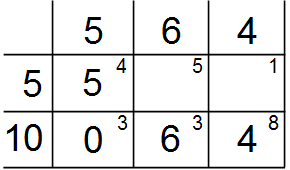
Остается клетка , которую можно заполнить единственно возможным значением 4.

В результате мы получили первый опорный план. Базисные переменные: . Свободные переменные: . Значение целевой функции:
.

Определение потенциалов

Определяем потенциалы . Для этого нужно найти любое решение системы уравнений, используя только заполненные клетки таблицы, то есть базисные переменные:
(Т.7) .

Запишем уравнения (Т.7) для заполненных клеток:
(Т.8)
Здесь 4 уравнения и 5 неизвестных. Поэтому одной переменной можно присвоить произвольное значение. Полагаем . Решаем систему (Т.8).
.

Находим оценки свободных клеток (то есть оценки свободных переменных) по формуле:
.

.

Поскольку есть отрицательная оценка , то план не оптимален. Вводим переменную с отрицательной оценкой в базис.

Переход к новому базису

Чтобы перейти к новому базису, в симплексном методе, мы выполняли линейные преобразования над системой ограничений. В транспортной задаче переход выполняется с помощью цикла.

Цикл с начальной вершиной в заданной пустой клетке – это ломаная, все вершины которой расположены в занятых клетках, кроме одной начальной вершины. И при этом две соседние вершины цикла расположены или в одной строке, или в одном столбце. 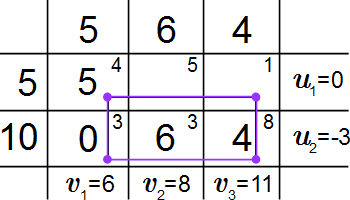Потенциалы и контур клетки (1,3).

Строим цикл для клетки . Пронумеруем его вершины, начиная со свободной клетки.

Переходим к новому базису, выполняя перераспределение поставок. Для этого находим минимальное значение поставки среди четных вершин цикла. В нашем случае это поставка 4 в клетке . В четных клетках уменьшаем поставки на 4, а в нечетных – увеличиваем на 4. Такое перераспределение поставок называют сдвигом по циклу. При этом поставка в клетке становится равной нулю. Ее мы выводим из базиса, а клетка становится заполненной, то есть входит в базис.

Второй опорный план.

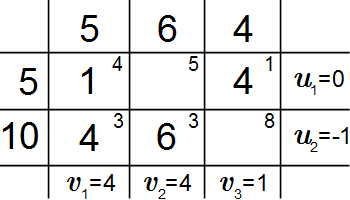
В результате получаем второй опорный план. Базисные переменные: . Свободные переменные: . Значение целевой функции:
.
Для первого опорного плана было . Мы видим, что значение целевой функции стало меньше.

Определение потенциалов нового плана

Определяем потенциалы для нового опорного плана. Запишем уравнения (Т.7) для заполненных клеток:
(Т.9)
Полагаем . Решаем систему (Т.9).
.

Находим оценки свободных клеток по формуле:
.

.

Поскольку отрицательных оценок нет, то план оптимален.

Наименьшее значение целевой функции . Оптимальный план показан в таблице 2 ⇑.

Использованная литература:
С. Гасс. Линейное программирование (методы и приложения). Москва, «Государственное издательство физико-математической литературы», 1961.
Общий курс высшей математики для экономистов. Под общей редакцией В. И. Ермакова. Москва, «ИНФРА-М», 2007.
К. Н. Лунгу. Линейное программирование. Руководство к решению задач. Москва, «ФИЗМАТЛИТ», 2005.
Д. Б. Юдин, Е. Г. Гольштейн. Задачи и методы линейного программирования. Москва, «Советское радио», 1961.

Автор: Олег Одинцов . Опубликовано: 08-04-2021

Источник