Что такое дискретный способ расчета

Дискретный период расчета показателей

В качестве дискретного периода расчета показателей принимается:

для прогноза социально-экономического развития организации на пять лет (стратегический план развития) – год;

для бизнес-плана развития предприятия на год – квартал;

для бизнес-плана инвестиционного проекта год (месяц).

Необходимость помесячного расчета показателей бизнес-плана инвестиционного проекта возникает во многих случаях по причине потребности более точного отражения динамики выдачи и погашения кредита: банки и лизинговые компании рассматривают помесячные расчеты кредитования и осуществления лизинговой операции. Кроме того, помесячный расчет инвестиционных затрат и чистого дохода позволяет получить более точный результат в определении показателей простого и динамического сроков окупаемости. Также, зачастую отдельные виды проектов на их операционной стадии имеют ярко выраженную сезонность в производстве, продажах и потреблении ресурсов. Например, тепловая энергия потребляется в большей мере в зимние месяцы и в меньшей степени в летний период. Поездки пассажиров в общественном транспорте имеют некоторую сезонную цикличность. Цены и объемы продаж многих видов продуктов питания изменяются по периодам зима, весна, лето, осень.

Экономические условия реализации проекта

Экономические условия реализации проекта выражаются через систему налогообложения, корректировку прогнозных показателей на уровень инфляции, пересчет ресурсов проекта через динамику курса (кросс-курса) валют.

Как правило, на уровень инфляции производится корректировка:

цен продажи продукции и оказания услуг;

цен закупок сырья, материалов, покупных изделий и комплектующих;

цен и тарифов на топливно-энергетические ресурсы;

цен и тарифов на промышленные услуги (транспортные услуги, ремонт оборудования, услуги связи и так далее).

При определении экономических условий реализации конкретного проекта следует иметь в виду, что действующая в Республике Беларусь система налогообложения представляет значительные льготы инвесторам.

Валюта расчета показателей

Расчеты показателей бизнес-плана производятся в национальной валюте (млн. белорусских рублей) или в свободно-конвертируемой валюте (долл. США, евро и так далее).

При разработке бизнес-плана инвестиционного проекта для получения инвестиционного кредита расчеты показателей, как правило, производятся в валюте кредитования. В то же время, если проект уже имеет достаточно продолжительную инвестиционную стадию своей реализации или осуществляется на действующем предприятии, то более точные расчеты могут быть осуществлены в национальной валюте, поскольку они не требуют пересчета показателей в валюту по среднему курсу дискретных периодов за предыдущие годы.

Норма дисконта

Определение нормы дисконта является одним из центральных моментов в бизнес-планировании. Данный показатель формирует динамику чистого дисконтированного дохода, динамический срок окупаемости, являющиеся важнейшими оценочными показателями эффективности инвестиционного проекта. Чистый дисконтированный доход характеризует интегральный эффект от реализации проекта. Он используется для оценки бизнеса доходным методом.

Норма дисконта может быть определена как средневзвешенная величина в зависимости от стоимости собственного и заемного капитала, привлекаемого в проект, а также иными способами, например, как средняя сложившаяся на рынке доходность по долгосрочным финансовым вложениям.

Число и содержание расчетных таблиц показателей

Минимально необходимое число и содержание таблиц, применяемых для расчета и прогнозирования показателей бизнес-плана, определяется соответствующими нормативно-методическими документами. В то же время, как правило, для точного и обоснованного выстраивания системы показателей, отображения технологических и отраслевых особенностей бизнеса, создаваемого через реализацию инвестиционного проекта, указанных таблиц бывает недостаточно. Поэтому требуется разработка дополнительных таблиц и их увязка с базовыми таблицами.

Разделение процесса реализации проекта на пусковые комплексы (этапы).

Зачастую, инвестиционный этап реализации проекта является достаточно продолжительным. Создаваемой производство включает несколько отдельных производств конечная продукция одного из которых является исходным сырьем (материалом) для другого. В этом случае целесообразно рассмотреть возможность разделения данного этапа на пусковые комплексы или законченные этапы (осуществить декомпозицию проекта) и вводить их раздельно таким образом, чтобы на каждом этапе обеспечить коммерческую эксплуатацию созданных на этапах объектов, что отражается в разрабатываемой модели. Это дает значительную экономическую выгоду за счет более ранней эксплуатации хотя бы части создаваемого хозяйственного комплекса.

Локализация проекта

Под локализацией проекта понимается разработка и реализация мер, направленных на максимально полное и эффективное использование возможностей национальных производителей в процессе осуществления как инвестиционной, так и операционной стадий, что должно найти отражение в модели и ее факторологическом наполнении.

Источник

Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.

Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.

Дискретность – это …

Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.

В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.

Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.

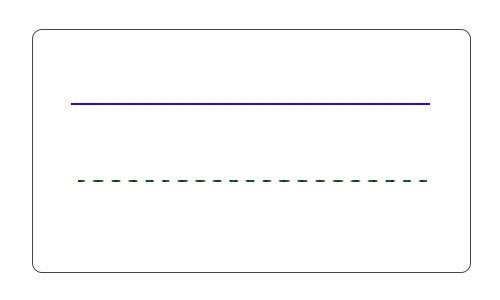
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:

Дискретность можно толковать следующим образом:

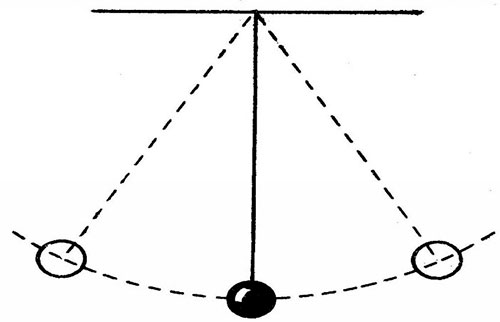
как меняющееся состояние между двумя и более стабильными положениями. К примеру, качающийся маятник: достигает точки А, затем вновь перемещается в точку В, и так до бесконечности, пока колебания не затихнут. Состояние маятника «в пути» можно рассматривать как дискретное состояние;

Далее проанализируем особенности применения термина в различных областях.

Дискретная математика

Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.

ДМ условно подразделяется на пять направлений:

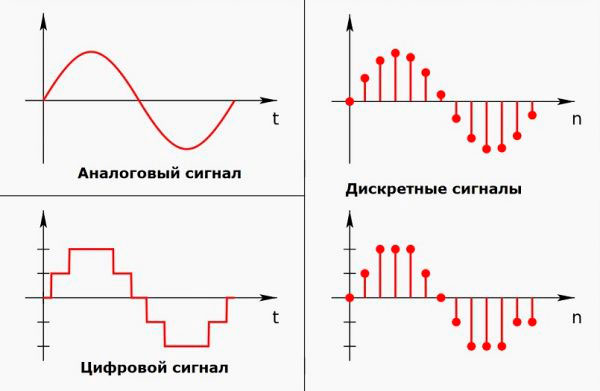
логика – наука о корректных рассуждениях. Пример логического заключения: если я закончил школу, то я выпускник этой школы. Логические заключения могут быть истинными (4 ˃ 2) и ложными (4 Цифровой и дискретный сигнал – это не одно и то же. Цифровой также состоит из отдельных значений, но не является прерывистым. Это можно проиллюстрировать на следующей схеме:

Дискретная величина

Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.

Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.

Дискретность в информатике

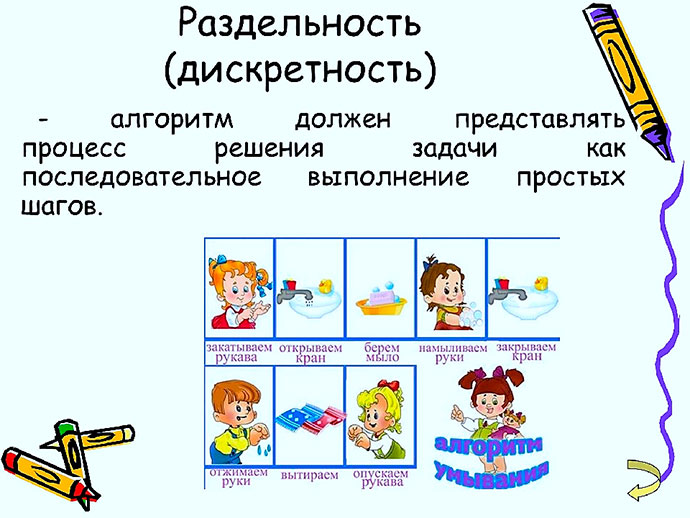
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).

Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.

Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):

Дискретная видеокарта

Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.

Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.

Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.

Дискретность в биологии

Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Благодарю за дискретное изложение материала

Источник

Основы дискретной математики

Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.

Об этой статье

Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!

ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?

Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.

Мы рассмотрим пять основных разделов в следующем порядке.

ЛОГИКА

Что такое логика?

Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.

Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).

Начнем с азов. Рассмотрим следующее высказывание на естественном языке:

«Если я голоден, я ем».

Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:

A => B (то есть из A следует B)

NB. Посылка и следствие являются суждениями.

Логические выражения

Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.

Например, 10 4 — ИСТИНА.

Логические операции

Суждение P — это утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).

Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).

Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.

Источник

Дискретный способ вычисления временных характеристик

Временные характеристики системы, описываемой векторно-матричным дифференциаль­ным уравнением состояния, можно получить, воспользовавшись дискретной аппрокси­мацией этого уравнения. Подобная аппроксимация основана на разбиении временной оси на достаточно малые отрезки. Тогда значения переменных состояния будут вычисляться в дискретные моменты времени t = 0,T, 2Т, ЪТ. где Тесть шаг дискретности по времени. Этот метод широко используется при численном анализе и при вычислениях на цифровых компьютерах. Если шаг дискретности Тявляется достаточно малым по сравнению с посто­янными времени системы, то точность вычислений будет вполне приемлемой.

Уравнение состояния линейной системы имеет вид:

Воспользуемся классическим определением производной:

Этим определением мы воспользуемся для вычисления значений х(/) при разбиении t на малые отрезки At = Т. Тогда, приняв аппроксимацию производной

подставим ее в уравнение (3.87) и получим:

Выразим отсюда х(г+7):

х(/ + Т) * 7Ax(f) + х(/) + 7Ви(/) = (7А + I) х(/) + 7Ви(/), (3.91)

где t разбито на малые отрезки длительностью Т. Поэтому время / принимает дискретные значения t = kT, k = 0, 1,2, 3. Тогда (3.91) будет записано в виде:

х[(А + 1)Z-] * (7А + 1)х (кТ) + ТВи (кТ). (3.92)

Таким образом, значение вектора состояния в (А+1)-й момент времени выражается через значения х и и в к-й момент времени. Выражение (3.92) можно записать иначе:

х(к + 1) *\i(T)x(k) + 7Bu(/c), (3.93)

где j/(7) = (7А +1), а символ Тв аргументах переменных опущен. Выражение (3.93) пока­зывает, что определение х(/) сводится к вычислению его дискретной аппроксимации х(А+1) на основании предыдущего значения х(к). Эта рекуррентная операция, известная как ме­тод Эйлера, представляет собой последовательную цепочку вычислений и очень просто реализуется на цифровых компьютерах. Для вычислений по формуле (3.87) могут быть ис­пользованы и другие методы численного интегрирования, например методы Рунге-Кутта. Некоторые методы интегрирования реализованы в среде MATLAB. Метод дискретного (численного) определения временных характеристик мы проиллюстрируем ниже на при­мере А’ІС-цепи (рис. 3.4).

Пример 3.6. Временные характеристики RLC-цепи

Вычислим временные характеристики. RLC-цепи с помощью дискретной аппроксимации урав­нения состояния, не прибегая к определению переходной матрицы состояния. Как и в примере 3.5, положим R = 3, L= 1 иС = 1/2. Тогда векторно-матричное уравнение состояния примет вид (см. уравнение 3.18):

Шаг дискретности Т мы должны выбрать достаточно малым, чтобы получить приемлемую точность аппроксимации производной (3.89) и, следовательно, как можно лучше приблизить вычисления по рекуррентной формуле (3.92) к точному решению уравнения состояния. Обыч­но Т выбирают так, чтобы он был по крайней мере вдвое меньше самой малой постоянной вре­мени системы. Учитывая то, что наименьшая постоянная времени системы равна 0,5 с [напом­ним, что характеристический полином системы имеет вид (s + l)(s + 2)], выберем значение

Т = 0,2 с. Заметим также, что с уменьшением шага дискретности пропорционально увеличива­ется количество вычислений. Итак, при Т= 0,2 с уравнение (3.92) принимает вид:

х(к + 1)« (0.2А+ I)x(£) + 0,2Ви(А). (3.95)

Предположим, что нас интересует реакция системы при*((0) = х2(0) = 1 и u(t) = 0. Реакция сис­темы в первый момент времени, т. е. при t = Т, или при к = 0, равна

Далее, при t = 2T= 0,4 с, или при к= 1:

Дальнейшие значения при к = 2, 3. 4. . вычисляются аналогично.

Сравним теперь точное значение реакции системы, полученное в предыдущем разделе с помо­щью переходной матрицы состояния, с приближенным значением, вычисленным в результате дискретизации времени. В примере 3.5 при Х|(0) = *2(0) = 1 мы получили точное решение для переменных состояния: x](t) = x2(t) = e

2′. В табл. 3.1 приведены вычисленные точные значе­ния Х|(0, а также приближенные значения при Т = 0,2 с и при Т = 0,1 с. В случае Г = 0.2 с ошиб­ка остается приблизительно постоянной и равной 0,07, что составляет 7% от начального значе­ния переменных состояния. При уменьшении 7’до 0,1 с ошибка также уменьшается приблизи­тельно до 3,5% от начального значения переменных состояния. Если взять Т = 0,05 с, то ап­проксимация решения в момент t = 0,2 с дает значение *,(/) = 0,655, и ошибка уменьшается до 1,5% от начального значения переменных состояния.

Точные значения x

Аппроксимация хі(0. Г =0,1 с

Ашгооксимаиия jcifr). Т— 0.2 с

Пример 3.7. Динамика эпидемического заболевания

Рассмотрим еще раз модель в переменных состояния, отражающую распространение эпидеми­ческого заболевания, с которой мы познакомились в примере 3.2. Полагая в уравнении состоя­ния (3.55) а = р = у = 1, получим:

Характеристическое уравнение системы [см. (3.57)] имеет вид s2 + 2s + 2 = 0, и, следовательно, его корни — комплексные. Определим динамику распространения заболевания, считая, что скорость появления новых восприимчивых к нему равна нулю, т. е. к, = 0. Скорость появления

новых инфицированных определим как и2(0) = 1 и и2(к) = 0 при к > 1; это означает, что в нача­льный момент времени появляется только один инфицированный (что эквивалентно импуль­сному входному воздействию). Постоянная времени, соответствующая комплексным корням, l/Cfo„ = I с, поэтому выберем Т = 0,2 с. (Заметим, что в действительности время может измеря­ться месяцами, а входное воздействие — тысячами человек.)

Запишем уравнение состояния в дискретной форме:

Реакция системы в первый момент времени t = Т, т. е. при к = 0 и при условии, что jtj(O) = х,(0) = х3(0) = 0, равна

После этого вход и2(к) при к > 1 становится равным нулю, и в момент t = 27’ реакция системы определяется как

Аналогично в момент t = 3T получим:

Последующие значения вычисляются так же просто. Разумеется, в действительности величина х, не может принимать отрицательные значения, но в нашем примере так получается из-за неа­декватности модели.

Метод дискретизации уравнения состояния оказывается чрезвычайно полезным при вычислении временных характеристик нелинейных систем. В этом случае уравнение со­стояния имеет общий вид:

где f есть функция (не обязательно линейная) вектора состояния х и вектора входа и. Век­тор f представляет собой матрицу-столбец функций от х и и. Если система является линей­ной по отношению к входным сигналам, то уравнение (3.104) принимает вид:

x = f(x,0 + Bu. (3.105)

Если система является стационарной, т. е. описывается дифференциальным уравне­нием с постоянными коэффициентами, то уравнение (3.105) принимает вид:

Рассмотрим уравнение (3.106) для нелинейной системы и получим его дискретную

аппроксимацию. Используя аппроксимацию производной в виде (3.89), запишем:

Полагая t = кТ, выразим отсюда х(А+1):

х(к +1) = х( к) + Т [f (х( к)) + Ви(А)].

Аналогично, для уравнения общего вида (3.104) дискретная аппроксимация записывается как

х(к +1) = (к) + ТІ [х(А), и(А), к. (3.109)

Далее мы рассмотрим систему из предыдущего примера с учетом того, что она явля­ется нелинейной.

Пример 3.8. Уточненная модель распространения эпидемического заболевания

Распространение эпидемического заболевания более точно описывается следующей системой нелинейных дифференциальных уравнений:

х2 = f>XfC2 — Ух2 + (3-110)

где взаимодействие между группами населения представлено нелинейным членом х, х2. Как и в предыдущем примере, будем считать, что а = Р = у =1, И|(/) = 0, и2(0) = 1 и и2(к) = 0 при

к> 1. Выберем шаг дискретности Т — 0,2 с и зададим начальные условия в виде хт(0) = [1 0 0].

Тогда, подставляя в уравнения (3.110) t-kT и

Выражая из этих уравнений х,(к+1) и помня, что Т = 0,2 с, получим: х,(к + 1) = 0,8.x,(/с) — 0,2х,(к)х2(к),

х2(к+ 1)= 0,8х2(к)+ 0,2л|(/с)л:2(Л) + d. hi^k) , (3.113)

х^(к + 1) = хъ(к) + 0,2х,(А) + 0,2х2(к).

Тогда в первый момент времени, при t = Т имеем:

*,(1) = 0,&х,(0)=0,8. х2(1) = 0,2и2(0) = 0,2,

Еще раз используя уравнения (3.113) и учитывая, что и2(1) = 0, получим: хі(2) = 0.8хіС1) — 0.2.ті(1)л2(1) = 0.608.

х2(2) = 0.8jc2(1) + 0,2х](1)х2(1) = 0,192, (3.114)

х3(2) = *з(1) + 0,2х,(1) + 0,2ї2( 1) = 0,40.

Аналогично, при / = 37” имеем:

*,(3) = 0,463, *2(3) = 0,177, х3(3) = 0,56.

Дальнейшие вычисления не вызывают проблем. Нетрудно видеть, что реакция нелинейной си­стемы существенно отличается от реакции ее линейной модели, рассмотренной в предыдущем примере.

Вычисление временных характеристик линейных систем легко производится путем либо (1) использования переходной матрицы состояния, либо (2) с помощью дискретной аппроксимации уравнения состояния. Для нелинейных систем наиболее подходящим яв­ляется метод дискретизации уравнения состояния, тем более, что он очень удобен при численных вычислениях на компьютере.

СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Требования к качеству системы в частотной области

Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …

Измерение частотных характеристик

Синусоидальный сигнал можно использовать для измерения частотных характеристик ра­зомкнутой системы управления. На практике это связано с получением графиков зависи­мости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …

Пример построения диаграммы Боде

Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отде­льно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …

Продажа шагающий экскаватор 20/90

Цена договорная
Используются в горнодобывающей промышленности при добыче полезных ископаемых (уголь, сланцы, руды черных и
цветных металлов, золото, сырье для химической промышленности, огнеупоров и др.) открытым способом. Их назначение – вскрышные работы с укладкой породы в выработанное пространство или на борт карьера. Экскаваторы способны
перемещать горную массу на большие расстояния. При разработке пород повышенной прочности требуется частичное или
сплошное рыхление взрыванием.
Вместимость ковша, м3 20
Длина стрелы, м 90
Угол наклона стрелы, град 32
Концевая нагрузка (max.) тс 63
Продолжительность рабочего цикла (грунт первой категории), с 60
Высота выгрузки, м 38,5
Глубина копания, м 42,5
Радиус выгрузки, м 83
Просвет под задней частью платформы, м 1,61
Диаметр опорной базы, м 14,5
Удельное давление на грунт при работе и передвижении, МПа 0,105/0,24
Размеры башмака (длина и ширина), м 13 х 2,5
Рабочая масса, т 1690
Мощность механизма подъема, кВт 2х1120
Мощность механизма поворота, кВт 4х250
Мощность механизма тяги, кВт 2х1120
Мощность механизма хода, кВт 2х400
Мощность сетевого двигателя, кВ 2х1600
Напряжение питающей сети, кВ 6
Более детальную информацию можете получить по телефону (063)0416788

Источник