Что такое арифметический способ решения задач 5 класс

Решение текстовых задач арифметическим способом.
презентация к уроку (5 класс) на тему

Презентация к уроку решение текстовых задач арифметическим способом . 5 класс

Скачать:

Вложение	Размер
reshenie_tekstovyh_zadach_arifmeticheskim_sposobom_morozova_e.v.ppt	1.6 МБ

Предварительный просмотр:

Подписи к слайдам:

Муниципальное общеобразовательное учреждение Средняя общеобразовательная школа № 2 г.Красный Кут Морозова Елена Владимировна

“ Учиться нелегко, но интересно». Я. Каменский .

Задача №1: В книге 40 страниц. Девочка прочитала в 3 раза больше, чем осталось прочитать. Сколько страниц осталось прочитать? Решение: 1 часть — осталось прочитать 3 части — девочка прочитала 1+3=4 части на 40 страниц 40:4=10 — осталось прочитать Ответ: 10

Задача №2: У хозяйки было 20 кур и цыплят. Кур меньше, чем цыплят в 4 раза. Сколько было кур, цыплят? Решение: 1 ч — куры 4 ч — цыплята Всего — 5 ч 20:5=4 (куры) 4х4=16 (цыплята ) Ответ: 4 и 16

Задачи для совместного решения

Задача №3: Старинная китайская задача (письменно): В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Узнать число фазанов и число кроликов. Решение: — Представьте, что наверх клетки, в которой сидят фазаны и кролики, мы положили морковку. Сколько ног в этот момент будет стоять на земле? Ответ: 23 и 12 35х2=70 Остальные не посчитаны – это передние лапы кроликов. Сколько их? 94-70=24 Сколько же кроликов? 24:2=12 А фазанов? 35-2=23 Но в условии задачи даны 94 ноги, где же остальные?

Задача №4: Старинная русская задача : Помещик, узнав, что корова стоит вчетверо дороже собаки и вчетверо дешевле лошади, захватил на ярмарку 200 рублей. На все эти деньги купил собаку, 2 коровы и лошадь. Сколько стоит собака, корова и лошадь? Решение: Повторив условие задачи, сделаем краткую запись: Цена собаки Мне нравится

Источник

Решение текстовых задач арифметическим способом

Разделы: Математика

Обучение решению текстовых задач играет важную роль в формировании математических знаний. Текстовые задачи дают большой простор для развития мышления учащихся. Обучение решению задач – это не только обучение технике получения правильных ответов в некоторых типичных ситуациях, сколько обучение творческому подходу к поиску решения, накопление опыта мыслительной деятельности и демонстрация учащимися возможностей математики в решении разнообразных задач. Однако при решении текстовых задач в 5-6 классах чаще всего используется уравнение. Но мышление пятиклассников еще не готово к формальным процедурам, выполняемым при решении уравнений. Арифметический способ решения задач имеют ряд преимуществ по сравнению с алгебраическим потому, что результат каждого шага по действиям нагляднее и конкретнее, не выходит за рамки опыта пятиклассников. Школьники лучше и быстрее решают задачи по действиям, чем с помощью уравнений. Детское мышление конкретно, и развивать его надо на конкретных предметах и величинах, затем постепенно переходить к оперированию абстрактными образами.

Работа над задачей предусматривает внимательное прочтение текста условия, вникания в смысл каждого слова. Приведу примеры задач, которые легко и просто можно решить арифметическим способом.

Задача 1. Для приготовления варенья на две части малины берут три части сахара. Сколько килограммов сахара нужно взять на 2 кг 600 г малины?

При решении задачи на “части” надо приучить наглядно представлять условие задачи, т.е. лучше опираться на рисунок.

1. 2600:2=1300 (г) — приходится на одну часть варенья;
2. 1300*3= 3900 (г) — сахара нужно взять.

Задача 2. На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках вместе стояло 120 книг. Сколько книг стояло на каждой полке?

1) 1+3=4 (части) — приходится на все книги;

2) 120:4=30 (книг) — приходится на одну часть ( книги на второй полке);

3) 30*3=90 (книг)- стояло на первой полке.

Задача 3. В клетке сидят фазаны и кролики. Всего в ней 27 голов и 74 ноги. Узнать число фазанов и число кроликов в клетке.

Представим, что на крышку клетки, в которой сидят фазаны и кролики, мы положили морковку. Тогда все кролики встанут на задние лапки, чтобы дотянуться до нее. Тогда:

1. 27*2=54 (ноги) — будут стоять на полу;
2. 74-54=20 (ног) — будут наверху;
3. 20:2=10 (кроликов);
4. 27-10=17 (фазанов).

Задача 4. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, а в кино – 21, а 5 человек не ходили ни на экскурсию, ни в кино. Сколько человек ходили и на экскурсию, и в кино?

Для анализа условия и выбора плана решения можно использовать “круги Эйлера”.

1. 30-5=25 (человек) – ходили или в кино, или на экскурсию,
2. 25-23=2 (человек) – ходили только в кино;
3. 21-2=19 ( человек) – ходили и в кино, и на экскурсию.

Задача 5. Три утенка и четыре гусенка весят 2 кг 500 г, а четыре утенка и три гусенка весят 2кг 400г. Сколько весит один гусенок?

1. 2500+2400=2900 (г) – весят семь утят и семь гусят;
2. 4900:7=700 (г) – вес одного утенка и одного гусенка;
3. 700*3=2100 (г) – вес 3 утят и 3 гусят;
4. 2500-2100=400 (г) – вес гусенка.

Задача 6. Для детского сада купили 20 пирамид: больших и маленьких – по 7 и по 5 колец. У всех пирамид 128 колец. Сколько было больших пирамид?

Представим, что со всех больших пирамид мы сняли по два кольца. Тогда:

1) 20*5=100 (колец) – осталось;

2) 128-100-28 (колец) – мы сняли;

3) 28:2=14 (больших пирамид).

Задача 7. Арбуз массой 20кг содержал 99% воды. Когда он немного усох, содержание воды в нем уменьшилось до 98%. Определите массу арбуза.

Для удобства решение будет сопровождаться иллюстрацией прямоугольников.

99% вода	1% сухое вещество
98% вода	2% сухое вещество

При этом желательно рисовать прямоугольники “сухого вещества” равными, потому что масса “сухого вещества” в арбузе остается неизменной.

1) 20:100=0,2 (кг) – масса “сухого вещества”;

2) 0,2:2=0,1 (кг) – приходится на 1% усохшего арбуза;

3) 0,1*100=10 (кг) – масса арбуза.

Задача 8. Гости спросили: сколько лет исполнилось каждой из трех сестер? Вера ответила, что ей и Наде вместе 28 лет, Наде и Любе вместе 23 года, а всем троим 38 лет. Сколько лет каждой из сестер?

1. 38-28=10 (лет) – Любе;
2. 23-10=13 (лет) – Наде;
3. 28-13=15 (лет) – Вере.

Арифметический способ решения текстовых задач учит ребенка действовать осознанно, логически правильно, потому что при решении таким способом усиливается внимание к вопросу “почему” и имеется большой развивающий потенциал. Это способствует развитию учащихся, формированию у них интереса к решению задач и к самой науке математике.

Чтобы сделать обучение посильным, увлекательным и поучительным, надо очень внимательно отнестись к выбору текстовых задач, рассматривать различные способы их решения, выбирая оптимальные из них, развивать логическое мышление, что в дальнейшем необходимо при решении геометрических задач.

Научиться решать задачи школьники смогут, лишь решая их. “Если вы хотите научиться плавать, то смело входите в воду, а, если хотите научиться решать задачи, то решайте их”,- пишет Д.Пойа в книге “ Математическое открытие”.

Источник

Урок математики в 5 классе «Арифметические способы решения текстовых задач»

Урок математики в 5 классе «Арифметические способы решения текстовых задач»

Дистанционное обучение педагогов по ФГОС по низким ценам

Вебинары, курсы повышения квалификации, профессиональная переподготовка и профессиональное обучение. Низкие цены. Более 13500 образовательных программ. Диплом госудаственного образца для курсов, переподготовки и профобучения. Сертификат за участие в вебинарах. Бесплатные вебинары. Лицензия.

Урок математики в 5 классе

«Арифметические способы решения текстовых задач»

Солдатова Светлана Анатольевна

учитель математики первой категории

МОУ Угличский физико-математический лицей

Образовательная: повторить, обобщить и систематизировать приёмы решения текстовых задач арифметическим способом.

Воспитательная: формировать личностные качества: сосредоточенность и внимание; настойчивость в достижение цели.

Развивающая: развивать познавательные интересы в процессе решения нестандартных задач, умения владеть математической терминологией, правильно и четко выражать мысль.

. Организационный момент.

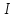
— Сегодня на уроке мы будем решать задачи. Они будут различны по типу, но объединять их будет то, что для решения будет отдано предпочтение арифметическому способу. А так как тема предыдущего урока –«Среднее арифметическое», то на уроке будут разобраны задачи на эту тему.

. Устный упражнения:

– Несколько задач я предлагаю вам решить устно, т.к. для их решения не требуется сложных вычислений, а способы решения вам уже знакомы.

а) (Задача-шутка) Шёл старик в Москву, повстречал 7 старушек: у каждой из них было по мешку, а в каждом мешке по коту. Сколько существ направлялось в Москву?

б) (Старинная индийская задача) Из четырёх пожертвователей второй дал вдвое больше первого, третий – втрое больше второго, а четвёртый — вчетверо больше третьего, а все вместе дали 132 монеты. Сколько монет дал первый?

132 монеты (на доске краткая запись задачи)

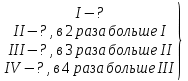
— Что удобно принять за 1 часть?

— Сколько всего монет частей приходится на 132 монеты? (1+2+6+24=33)

132:33=4 (м) – у первого жертвователя.

в) У Олега и Димы вместе72 марки. Сколько марок у каждого, если у Олега на 6 марок меньше?

— Определите тип задачи. (Нахождение двух чисел по их сумме и разности)

— Назовите все возможные способы решения данной задачи.

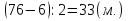
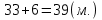
1способ: – у Олега.

— у Димы.

(используется понятие «удвоенное меньшее число»)

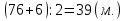
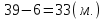
2 способ: — у Димы.

— у Олега.

(используется понятие «удвоенное большее число»)

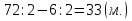
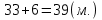
3 способ: — у Олега.

— у Димы.

(используются понятия «полусумма» и «полуразность», так называемый «старинный способ»)

Решение задач по теме «Среднее арифметическое».

а) Настя и Ксюша поделили грибы поровну. У каждой стало по 22 гриба. Сколько грибов набрала каждая, если первоначально у Насти было на 8 грибов больше?

— Какие способы решения вы предлагаете?

— Какой способ самый рациональный по вашему мнению? (среднее арифметическое – это полусумма для двух чисел).

1) (г.) — полуразность.

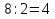
Ответ: 26 грибов, 18 грибов.

б) Среднее арифметическое трёх чисел 0,43. Первое число в 1,5 раза больше второго, а третье в 1,8 раза больше второго. Найдите первое число.

1) (г.) – приходится на сумму трёх чисел.

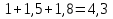
2) – число.

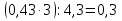
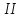
3) – число.

. Задачи на «предположение»

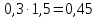
а) (Старинная китайская задача). В клетке находятся 35 фазанов и кроликов. Известно, что у них 94 ноги. Узнайте число фазанов и число кроликов.

— Предположим, что в клетке сидели бы только фазаны. Сколько ног имели бы 35 фазанов? (дети записывают решение в тетради, а учитель на доске)

1) 2 35=70(н.) – если бы было 35 фазанов

— Почему ног больше? (Среди них есть кролики, у которых 4 ноги).

— Если мы одного фазана заменим на кролика, на сколько увеличится количество ног?

2) 4-2=2(н) — на столько ног больше у одного кролика, чем у одного фазана.

— А на сколько ног всего больше?

3) 94-70=24(н.) на столько всего больше ног.

Как узнать количество кроликов?

4) 24:2=12 — кроликов.

5) 35-12=23 – фазанов.

Ответ: 12 кроликов, 23 фазана.

-Есть очень интересное рассуждение, найденное в старых источниках. Представьте, что на верх клетки, в которой сидят фазаны и кролики, мы положим морковку. Все кролики встанут на задние лапки, чтобы дотянуться до морковки.

— Сколько ног в этот момент будут стоять на земле?

— А где остальные?

— Сколько же кроликов?

— Сравните наше рассуждение с записью решения в тетради.

— А теперь попробуйте самостоятельно решить следующую задачу.

б) В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе

19 голов и 46 ног?

30 голов и 74 ноги? (по вариантам, 2 человека у доски с последующей проверкой)

1)2 19=38(н.) – если бы все были куры.

2) 46-38=8(н) — на столько ног больше.

Ответ: 4 овцы, 15 кур.

1)2 30=60(н.) – если бы все были куры.

2) 74-60=14(н) — на столько ног больше.

Ответ: 7 овец, 23 куры.

1) (г.) – приходится на сумму трёх чисел.

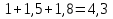
2) – число.

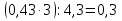
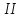
3) – число.

. Разные задачи (старинные)

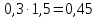
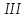
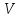
а) Лошадь вместе с седлом стоит 235 р., лошадь вместе со сбруей стоит 250 р., сбруя вместе с седлом стоит 135 р. Сколько стоит лошадь, сколько сбруя и сколько седло?

1) 250+235+135=620(р.) — стоят 2 лошади, 2 сбруи и 2 седла.

2) 620:2 =310(р.) – стоит лошадь, седло и сбруя.

3) 310-235=75(р.) – стоит сбруя.

4) 250-75=175(р.) – стоит лошадь.

5) 235-175=60(р.) – стоит седло.

Ответ: 175 р., 75.р., 60 р.

б ) Крестьянин хочет купить лошадь и для этого продаёт рожь. Если он продаст 15 ц ржи, то ему не хватит для покупки лошади 80 р., а если он продаст 20 ц ржи, то у него останется 110 р. Сколько стоит лошадь?

2) 80 +110=190(ц) стоят 5ц ржи.

3)190:5=38(р.) стоит 1ц ржи.

4) 38 20-110=650(р.) – стоит лошадь.

. Подведение итогов.

Домашнее задание.

1) На лугу паслось несколько коров. У них ног на 24 больше, чем голов. Сколько коров паслось на лугу ?

2) Старинная задача. За 1000 р. Я купил 44 коровы – по 18 р. и по 26 р. Сколько тех и других?

Шевкин А. В. Обучение решению текстовых задач в 5-6 классах. – М.: Галс плюс,1998.

Источник