Что собой представляет способ группировки

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Источник

Сводка и группировка статистических данных

3.2. Метод группировок в статистике

Под статистической группировкой понимается распределение единиц наблюдения по группам по одному или нескольким признакам. Эти признаки называются группировочными. В зависимости от задач исследования строят типологические, структурные и аналитические группировки.

Типологическая группировка представляет собой распределение единиц наблюдения качественно неоднородной совокупности по социально-экономическим типам, классам, качественно однородным группам. Например, распределение совокупности предприятий по формам собственности (табл. 3.1); отраслям экономики; размеру бизнеса — малые, средние и крупные предприятия (отнесение к ним идет сразу по нескольким критериям); банков — на государственные и коммерческие и т.д. Основная задача типологической группировки — идентификация и описание типов исследуемого явления. Число выделяемых групп определяется количеством типов, классов, однородных групп, т.д. самим характером явления.

Таблица 3.1. Распределение предприятий и организаций по формам собственности на 1 января 2006 г.

Форма собственности	Число предприятий и организаций, тыс.
Государственная	160
Муниципальная	252
Собственность общественных и религиозных объединений (организаций)	252
Частная	3 838
Прочие формы собственности, включая смешанную российскую, иностранную, совместную российскую и иностранную	265
Всего	4 767

Источник: Россия в цифрах. 2006: Крат. стат. сб. / Росстат. М., 2006. С. 167.

При структурной группировке разделение единиц однородной совокупности на группы происходит с целью выявления ее структуры по одному из признаков. Например, распределение наемных работников по полу, возрасту; распределение предприятий по численности работающих и т.д. Примером структурной группировки являются данные табл. 3.2.

Таблица 3.2. Структура работников по стажу работы на предприятии

Стаж работы, лет	Число работников	Число работников в процентах к итогу
До 2	10	5
2-4	20	10
4-6	30	15
6-8	80	40
8 и более	60	30
Итого	200	100

Важную роль в статистическом анализе играют аналитические группировки. С их помощью определяют наличие связи между признаками и ее направление. При этом один из признаков является результативным, а другой — факторным. Результативный признак меняется под воздействием факторного признака.

При построении аналитической группировки в качестве группировочного признака всегда выбирают факторный признак. В каждой выделенной группе рассчитывают среднее значение результативного признака. Например, в табл. 3.3 компании сгруппированы по величине затрат на рекламу. В каждой группе определен средний размер товарооборота. Из таблицы видно, что чем больше внимания компании уделяют рекламе, тем значительнее результаты их деятельности, выражающиеся в объеме товарооборота.

Таблица 3.3. Распределение компаний по затратам на рекламу и объему товарооборота

Затраты на рекламу в год, млн руб.	Число компаний	Объем товарооборота в среднем на одну компанию, млн руб.
До 3	5	300
3-5	20	305
5-7	15	315
7 и более	10	320
Итого	50	311

Связь между признаками называется прямой , если с ростом значений факторного признака увеличиваются значения результативного признака. Связь является обратной, если увеличение значений факторного признака приводит к уменьшению значений результативного признака. В нашем примере рост затрат на рекламу вызвал увеличение объемов товарооборота, значит между этими признаками наблюдается прямая связь .

Наряду с группировками в статистическом анализе используются классификации. Классификация — это общепринятое, традиционно применяемое, часто официально установленное разбиение совокупности на группы, являющееся определенным стандартом, при котором единицам наблюдения предъявляются строгие требования относительно их соответствия той или иной группе. В основе классификаций лежит качественный признак. К наиболее известным относятся классификации отраслей экономики, административно-территориального деления, экономических регионов, видов экономической деятельности и др. Классификации не являются чем-то стабильным, в соответствии с экономическими и политическими изменениями меняются и они.

В зависимости от количества признаков, по которым проводится группировка, различают простые и сложные группировки. Если группировка проводится по одному признаку, то она называется простой (см. табл. 3.1, 3.2). Если единицы совокупности группируются сразу по двум или более признакам, то такая группировка называется сложной. При этом внутри групп, образованных по одному признаку, единицы совокупности подразделяются на подгруппы по другому признаку. Примером сложной группировки является группировка учащихся на потоке по двум признакам — полу и возрасту. Ее результаты могут быть представлены в виде таблицы (табл. 3.4).

Таблица 3.4. Распределение учащихся на потоке по полу и возрасту

Возраст, лет	Пол	Итого
мужчины	женщины
До 14	10	8	18
15	8	9	17
16	12	13	25
17 и более	11	10	21
Итого	41	40	81

Вторичная группировка данных. На практике часто возникают ситуации, когда по имеющимся сгруппированным данным требуется построить новую группировку. При этом, как правило, массив первичных данных оказывается недоступным. Тогда прибегают к методам вторичной группировки данных.

Вторичной группировкой называется перегруппировка уже сгруппированных данных без обращения к массиву первичных данных. Для этой цели применяются два подхода: объединение первоначальных интервалов, если границы новых и старых групп совпадают, и долевая перегруппировка данных при несовпадении границ.

Метод объединения первоначальных интервалов продемонстрируем на следующем примере. Предположим, что исходные данные представляют собой ряд, приведенный в табл. 3.5.

Таблица 3.5. Распределение работников фирмы по размеру заработной платы

Номер интервала	Заработная плата, руб.	Численность работающих, чел.
1	2 000-3 000	16
2	3 000-4 000	40
3	4 000-5 000	65
4	5 000-6 000	58
5	6 000-7 000	44
6	7 000 и выше	17
Итого	—	240

Перегруппируем данные и образуем новые интервалы: «2000-4000», «4000-6000», «6000 и выше». Поскольку границы новых и старых интервалов совпадают, легко видеть, что в первый новый интервал «2000-4000» попадут работники первого и второго интервалов исходной группировки (16 + 40 = 56 чел.), во второй новый интервал — работники третьего и четвертого интервалов исходной группировки (65 + 58 = 123 чел.), в третий новый интервал — работники двух последних интервалов (44 + 17 = 61 чел.). Результаты перегруппировки представлены в табл. 3.6.

Таблица 3.6. Распределение работников фирмы по размеру заработной платы (вторичная группировка)

Номер интервала	Заработная плата, руб.	Численность работающих, чел.
1	2 000-4 000	56
2	4 000-6 000	123
3	6 000 и выше	61
Итого	—	240

Долевая перегруппировка базируется на принципе равномерности распределения единиц наблюдения внутри границ интервальных групп. В результате ее проведения рассчитывают, какая часть единиц наблюдения перейдет из старой интервальной группы в новую.

Пример 3.1. «Перегруппируем данные табл. 3.5 и образуем новые интервалы: «2000-3400»; «3400-4800»; «4800-6200»; «6200 и выше». Распределим единицы совокупности по новым интервалам.

В первый новый интервал войдут из исходной группировки все единицы первого интервала и часть единиц из второго интервала. Эту часть мы определяем следующим образом. Новая граница «3400» разбивает второй интервал на два отрезка: «3000-3400» и «3400-4000». Находим, какую долю составляет длина отрезка «3000-3400» от длины второго интервала. Она равна 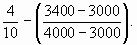Значит, от 40 единиц, находившихся во втором интервале исходной группировки, следует взять для нового первого интервала 16 единиц Тогда первый новый интервал будет содержать 32 единицы (16 + 16).

Во второй новый интервал войдут оставшиеся от второго интервала исходной группировки 24 единицы (40 — 16) и часть единиц из третьего интервала. Для этого мы находим, какую долю составляет отрезок «4000-4800» от длины третьего интервала «4000-5000». Она равна Значит, от 65 единиц следует взять для второго нового интервала 52 единицы Итак, второй интервал новой группировки будет содержать 76 единиц (24 + 52).

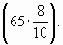
В третий интервал вторичной группировки войдут оставшиеся 13 единиц (65 — 52 = 13) третьего интервала исходной группировки, все единицы ее четвертого интервала (58 ед.) и 9 единиц пятого интервала

В последний интервал новой группировки войдут оставшиеся 35 единиц (44 — 9 = 35) пятого интервала и все 17 единиц последнего интервала, т.е. 52 единицы (35 + 17).

При проверке правильности расчетов видим, что сумма единиц совокупности осталась равной 240.

Результаты вторичной группировки приведены в следующей таблице.

Источник