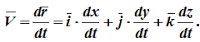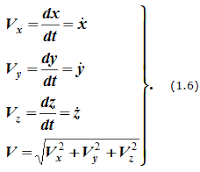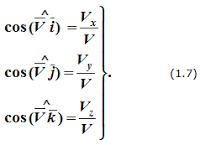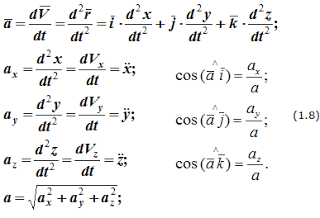Что необходимо знать при координатном способе задания движения точки тест

iSopromat.ru

При координатном способе задания движения точки в выбранной системе координат задаются координаты движущейся точки как функции от времени.

В прямоугольной декартовой системе координат это будут уравнения:

Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

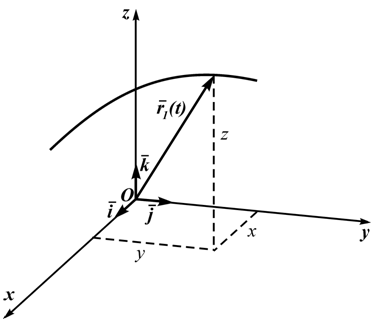
Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

Направление вектора скорости определяется с помощью направляющих косинусов:

Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

Аналогичны формулы для определения ускорения точки:

Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Координатный способ задания движения точки

Введение

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.

Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):

Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.

Определение кинематических величин

Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .

Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.

Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .

Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .

Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Пример решения задачи

Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки:
, см;
, см.

Решение

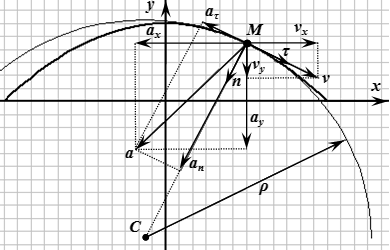
Определение вида траектории

Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.

Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .

Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;

Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .

Строим параболу по точкам.

0	6
± 3	5,625
± 6	4,5
± 9	2,625
± 12	0

Определяем положение точки в момент времени .
;
.

Определение скорости точки

Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.

Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.

Определение ускорения точки

Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.

Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.

Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .

Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.

Радиус кривизны траектории:
.

Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .

Определение остальных величин

При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .

Определим остальные величины.

Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:

.
Вектор нормального ускорения:

.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:

.

Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:

.

Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020

Источник

Контрольные тесты по теоретической механике «Раздел: кинематика».

Контрольные тесты по теоретической механике раздел «Кинематика»

Какие способы задания движения точки применяются в кинематике?

Что необходимо знать при естественном способе задания движения точки ?

1. Систему отсчета, траекторию движения, закон движения точки по траектории

2.Траекторию движения точки

3.Закон движения точки

4.Траекторию движения точки и начало отсчета

Что необходимо знать при векторном способе задания движения точки ?

2.Векторный закон движения точки

3.Траекторию, систему координат

4.Траекторию движения точки

Что необходимо знать при координатном способе задания движения точки ?

Траекторию движения точки

Траекторию, систему координат

Уравнения движения точки по траектории

Как направлен вектор скорости криволинейного движения точ ки по отношению к траектории?

1.Является касательным к траектории и напрвлен в сторону движения точки

2 .Является касательным к траектории и напрвлен в сторону противоположную движения точки

3. Является касательным к траектории

4. Напрвлен в сторону движения точки

5.Это скалярная величина

Чему равны проекции вектора скорости точки на оси декарто вых координат?

1.Первым производным от функции декартовых координат по времени

5.Производной от вектора скорости по времени

К ак направлен вектор ускорения криволинейного движения точ ки по отношению к траектории?

1.В сторону выпуклости траектории

2.В сторону вогнутости траектории

3.В сторону движения точки

4.По касательной к траектории

5.В сторону противоположную движения точки

Чему равны проекции вектора ускорения точки на оси декарто вых координат?

1.Вторым производным от функции декартовых координат по времени

2.Первым производным от функции проекций скоростей по времени

5.Проекции вектора скорости

В каких движениях касательное ускорение точки равно нулю?

1.В прямолинейном равномерном

2.В криволинейном равномерном

3. В криволинейном равноускоренном

4. В прямолинейном равнозамедленном

5. В прямолинейном равноускоренном

В каких движениях равно нулю нормальное ускорение?

В прямолинейном равномерном

В прямолинейном равноускоренном

В прямолинейном равнозамедленном

В криволинейном равноускоренном

В криволинейном равномерном

Какое движение твердого тела называется поступательным?

1.Движение по прямой

2.Движение по кривой

3.Когда любая прямая, связанная с телом, перемещается оставаясь параллельной

4.Движение по окружности

5.Когда все точки тела движутся по одинаковым траекториям

Какое движение твердого тела называется движением вокруг неподвижной оси?

Что называется угловой скоростью тела?

1. Это векторная величина, которая характеризует изменение угла поворота тела с течением времени

2. Это скалярная величина, которая характеризует изменение угла поворота тела с течением времени

3.Это скалярная величина, которая определяется первой производной от угла поворота тела по времени

4.Это вектор, направленный перпендикулярно радиусу вращения

Что называется угловым ускорением тела?

1. Это скалярная величина, которая определяется первой производной от угла поворота тела по времени

2. Это векторная величина, которая характеризует изменение угла поворота тела с течением времени

3. Это векторная величина, которая характеризует изменение угловой скорости тела с течением времени, как по величине, так и по направлению

4. Это скалярная величина, которая определяется второй производной от угла поворота тела по времен

5.Это векторная величина, которая определяется первой производной от угловой скорости тела по времени

Какое вращение твердого тела называется равномерным ?

1.Вращение с постоянной угловой скоростью

2. Вращение с постоянным угловым ускорением

3. Вращение с переменной угловой скоростью

4.Вращение с переменным угловым ускорением

Какое вращение твердого тела называется равнопеременным?

1. Вращение с переменным угловым ускорением

2. Вращение с переменной угловой скоростью

3. Вращение с постоянным угловым ускорением

4. Вращение с переменным угловым ускорением и угловой скоростью

Какая зависимость существует между угловой скоростью вра щающегося тела и числом его оборотов в минуту?

Как изображается угловая скорость тела в виде вектора?

1.Вектор направлен вдоль оси вращения, чтобы глядя с его конца был виден поворот тела против хода часовой стрелки

2. Вектор направлен вдоль оси вращения, чтобы глядя с его конца был виден поворот тела по ходу часовой стрелки

3.Вектор направлен перпендикулярно оси вращения

4.Вектор направлен параллельно оси вращения

Как выражается зависимость между угловой скоростью вращаю щегося тела и линейной скоростью какой-нибудь точки этого тела?

1.Линейная скорость точки определяется произведением угловой скорости тела на радиус вращения точки

2. Линейная скорость точки определяется произведением углового ускорения тела на радиус вращения точки

Как выража е тся касательное ускорени точки твердого тела, вращающегося вокруг неподвижной оси?

1.Определяется произведением углового ускорения тела на радиус вращения точки

2. Определяется произведением угловой скорости тела на радиус вращения точки

3. Определяется произведением квадрата угловой скорости тела на радиус вращения точки

Как выража е тся нормальное ускорения точки твердого тела, вращающегося вокруг неподвижной оси?

1.Произведением квадрата угловой скорости тела на радиус вращения точки

2. .Произведением угловой скорости тела на радиус вращения точки

3. .Произведением углового ускорения тела на радиус вращения точки

Как выражается основное свойство рядовой передачи ?

1.Угловые скорости колес в рядовой передачи обратно пропорциональны радиусам зацепления

2. Угловые скорости колес в рядовой передачи пропорциональны радиусам зацепления

3. Угловые скорости колес в рядовой передачи равны радиусам зацепления

Какое движение твердого тела называется плоским, или плоскопараллельным?

1.Когда все точки тела движутся в параллельных плоскостях относительно неподвижной плоскости

2.Это поступательное движение

3.Это вращательное движение

4.Все точки этого тела движутся по окружностям

5.Все точки этого тела двжутся по прямой

На какие два движения можно разложить плоскопараллельное движение твердого тела?

1.На прямолинейные и криволинейное

2.На прямолинейное и криволинейные

3.На поступательное и вращательное

4.На поступательное и криволинейное

Что называется мгновенным центром скоростей плоской фигу ры, движущейся в своей плоскости?

1.Это центр тяжести плоской фигуры

2.Это точка неподвижной плоскост

3.Это точка плоской фигуры скорость которой в данный момент времени равна нулю

4. Это точка плоской фигуры ускорение которой в данный момент времени равна нулю

Как можно найти положение мгновенного центра скоростей плоской фигуры, движущейся в своей плоскости?

1.Это точка пересечения перпендикуляров, восстановленных к векторам скоростей двух точек этой фигуры

2.Это точка на перпендикуляре восстановленном к вектору скорости любой точки плоской фигуры, длина которого равна отношению численного значения этой скорости к угловой скорости вращения фигуры

3. Это центр тяжести плоской фигуры

4.Это мгновенный центр вращений

Суммой каких двух составляющих скоростей является абсо лютная скорость произвольно выбранной точки плоской фигуры, дви жущейся в своей плоскости?

1.Это векторная сумма скорости полюса и вращательной скорости точки плоской фигуры вокруг полюса

2.Это сумма скоростей центра тяжести и вращательной скорости точки плоской фигуры вокруг полюса

3.Это сумма скорости и ускорения центра тяжести фигуры

4. Это алгебраическая сумма скорости полюса и вращательной скорости точки плоской фигуры вокруг полюса

Каковы будут скорости точек плоской фигуры в том случае, когда мгновенный центр скоростей этой фигуры окажется в бесконеч ности?

3.Скорость одной точки от другой будет отличаться в два раза

Как связаны скорости точек плоской фигуры ?

1.Скорости точек плоской фигуры прямо пропорциональны их расстояниям до мгновенного центра скоростей

2. Скорости всех точек плоской фигуры равны между собой

3. Скорости точек плоской фигуры обратно пропорциональны их расстояниям до мгновенного центра скоростей

4. . Скорости всех точек плоской фигуры равны нулю

Как определить угловую скорость плоской фигуры ?

1.Угловая скорость плоской фигуры всегда равна нулю

2.Равна произведению скорости любой точки на расстояние до мгновенного центра скоростей

3.Необходимо линейную скорость любой точки плоской фигуры разделить на соответствующее расстояние до мгновенного центра скоростей

4.Взять производную от скорости любой точки плоской фигуры по времени

Где будет находиться мгновенный центр скоростей у катящегося колеса по плоскости без проскальзования ?

1.В центре тяжести

4.В точке контакта колеса с плоскостью

Чему будет равна скорость точки А, если скорость центра катящегося колеса без проскальзования равна 10м/с ?

Какое движение точки называется относительным?

1.Движение точки относительно подвижной системы координат

2.Движение точки относительно движущегося тела

3.Движение тела относительно неподвижной системы координат

Какое движение точки называется переносным?

1.Движение точки вместе с телом

2.Движение точки относительно неподвижной системы координат

3. Движение точки относительно движущегося тела

4. Движение точки относительно подвижной системы координат

Какое движение точки называется абсолютным, или составным?

1.Это движение точки относительно неподвижной системы координат

2.Это сложное движение состоящее из относительного и переносного движений

3. . Движение точки относительно движущегося тела

4. Движение точки относительно подвижной системы координат

В чем состоит теорема о сложении скоростей?

1.Абсолютная скорость точки равна переносной скорости

2. Абсолютная скорость точки равна относительной скорости

3 Абсолютная скорость точки складывается из алгебраической суммы относительной и переносной скоростей

4. Абсолютная скорость точки складывается из векторной суммы относительной и переносной скоростей

В чем состоит теорема о сложении ускорений точки в том случае, когда переносное движение является поступательным ?

1 Абсолютное ускорение точки равно переносному ускорению

2. Абсолютное ускорение точки равно относительному ускорению

3. Абсолютное ускорение точки складывается из алгебраической суммы относительного и переносного ускорений

4. Абсолютное ускорение точки складывается из векторной суммы относительного и переносного ускорений

Основные единицы измерения в кинематике ?

Траекторией движущейся точки является

Окружностями будут траектории точек движущегося тела при

Положение движущейся точки можно определить, если

1 .И звестен закон

2 . И звестна траектория

3 .И звестен пройденный путь

4 .И звестно время

Физический смысл скорости

1 .П риращение пути в единицу времени

2 .П риращение пути на единицу длины

3 .П ервая производная от закона движения

4 .Т ангенс угла наклона касательной к графику пути к оси времени

Равномерное прямолинейное движение точки возможно только

1 .П ри отсутствии сил

2 .П ри действии постоянной силы

3 .П ри дейстрвии только сил трения

4 .В безвоздушном пространстве

Геометрический смысл скорости

1 .П риращение пути в единицу времени

2 .П риращение пути на единицу длины

3 .П ервая производная от скорости

4 .Т ангенс угла наклона касательной к графику пути

Равнопеременное прямолинейное движение точки происходит при

1 .П остоянной скорости

2 .П остоянном ускорении

3 .П оступательном движении тела

4 .К олебательном движении

Если движение точки задано координатным способом, то для нахождения уравнения траектории движения

1 .И сключить из уравнений движения время

2 . По теореме Пифагора

3 . Построить график движения

4 .Н айти производые по времени

Если движение точки задано координатным способом, то для нахождения проекции скорости на оси необходимо

1 . Исключить из уравнений движения время

2 . По теореме Пифагора

3 . Построить график движения

4 . Н айти производые по времени

Движение точки задано координатным способом.

1 .И сключить из уравнений движения время

2 .Н айти вторые производные по времени

3 .Н айти первые производные по времени

4 .П остроить график ускорений

Касательное ускорение меняет скорость по

4.П о величине и направлению

Нормальное ускорение меняет скорость по

3 .П о величине и направлению

Точка движется равномерно по окружности радиуса 4 м со скоростью 10 м/с. Полное ускорение при этом равно

Поступательное движение твердого тела можно рассматривать как движение

1 .Л юбой его точки

3 .П о окружности

4 .П о любой кривой

Для всех точек тела при поступательном движении равны

При вращательном движении твердого тела остаются неподвижными минимум точек

Единица измерения угловой скорости

1 .Р адиан в секунду

2 .Г радус в секунду

3 .М етр в секунду

4 .С антиметр в секунду

Точка движется вдоль иси ОХ. Скорость точки направлена:

1 .П араллельно оси Ox

2 .П араллельно оси Oy

3 .П араллельно оси Oz

4 .Н епараллельно осям Ox, Oy, Oz

При пуске паровой турбины угол поворота ее диска изме-

няется по закону

Угловая скорость диска паровой турбины при t =1 с равна :

Точка А шкива, лежащая на его ободе, движется со скоро-

стью 50 см/с, а некоторая точка В, взятая на одном радиусе с

точкой А, движется со скоростью 10 см/с. Расстояние АВ=20см.

Угловая скорость шкива равна (рад/с):

При пуске паровой турбины угол поворота ее диска изме-

няется по закону

Скорость точки диска паровой турбины на расстоянии 1м от

оси вращения при t =1 , равна (м/с):

Колесо радиуса 0,5м катится по горизонтальной прямой

без скольжения. Скорость центра колеса постоянная и равна 1м/с.

Угловая скорость колеса равна (рад/с):

Может ли быть поступательным движением у шатуна в кривошипно-ползунным механизмом ?

Какое движение совершает кривошип в кривошипно-шатунном механизме ?

Курс повышения квалификации

Охрана труда

• Сейчас обучается 94 человека из 45 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 344 человека из 67 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 175 человек из 48 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-425343

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник