- Соответствия между множествами
- Понятие соответствия между множествами
- Тема 3. Понятие соответствия Содержание
- 1. Понятие соответствия между множествами
- Рассмотрим примеры соответствий, изучаемых в начальном курсе математики.
- 2. Способы задания соответствий
- 3. Соответствие обратное данному
- §8. Понятие соответствия между множествами. Способы задания соответствий
- Лекция 8. Соответствия между элементами двух множеств. Определение соответствия между элементами двух множеств. Взаимно однозначные соответствия.
Соответствия между множествами
Изучая окружающий нас мир, математика рассматривает не только его объекты, но связи между ними. Эти связи называют зависимостями, соответствиями, отношениями, функциями. Например, при вычислении длин предметов устанавливаются соответствия между предметами и числами, которые являются значениями их длин; при решении задач на движение устанавливается зависимость между пройденным расстоянием и временем при условии, что скорость движения постоянна. Начальная частная школа помогает учащимся устанавить соответствие между заданными выражениями и их числовыми значениями, между числом, характеризующим площадь данной фигуры, и самой этой фигурой и т.п.
Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами P, S, T, R и др. Если xSy – соответствие между элементами множеств X и Y, то, соглаcно определению, S

Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами X= и Y= можно задать: 1) при помощи предложения с двумя переменными: a Просмотров 82 152 Комментариев 2
Источник
Понятие соответствия между множествами
В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике этих взаимосвязей.
Рассмотрим примеры соответствий, изучаемых в начальном курсе математики.
Пример 1. а) (17 – 1) : 4; б) (12 + 18) : (6-6); в) 2´7 + 6. Пример 2. 1) 2+х =6; 2) х-7=4; 3) 2х=8.
В первом примере мы установили соответствие между заданными выражениями и их числовыми значениями. Во втором выяснили, какое число является решением уравнения.
Все эти соответствия имеют общее – во обоих случаях мы имеем два множества: в первом – это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором – это множество из трех уравнений и множество Nнатуральных чисел.
Связь (соответствие) между этими множества можно представить наглядно, при помощи графов.
| а· б· в· |
| ·4 ·20 |
| 1· 2· 3· |
| ·4 ·11 |
N 1 N2
Полученные множества показывают, что любое соответствие между двумя множествами Х и У можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары – это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
Определение. Соответствием между множествами Х и У называется всякое подмножество декартова произведения этих множеств.Соответствия принято обозначать буквами R, P, F, T и др.
2. Способы задания соответствий
Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либоперечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества.
Пример. Соответствие между множествами Х = <1, 2, 4, 6>и У = <3, 5>можно задать: 1) при помощи предложения с двумя переменными: а -1 между множествами У и Х называется обратным данному, если у S -1 х тогда и только тогда, когда х S у. Соответствия S и S -1 называют взаимно обратными.
Выясним особенности их графиков. Построим график соответствия S =
Источник
Тема 3. Понятие соответствия Содержание
Понятие соответствия между множествами.
Способы задания соответствий.
Соответствие обратное данному.
Взаимно однозначное соответствие.
Равномощные множества. Счетные множества.
Основная литература 7, 10, 11, 16, 23, 33, 34;
Дополнительная литература 1, 10, 14, 74
1. Понятие соответствия между множествами
В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике этих взаимосвязей.
Рассмотрим примеры соответствий, изучаемых в начальном курсе математики.
Пример 1. а) (17 – 1) : 4; б) (12 + 18) : (6-6); в) 27 + 6. Пример 2. 1) 2+х =6; 2) х-7=4; 3) 2х=8.
В первом примере мы установили соответствие между заданными выражениями и их числовыми значениями. Во втором выяснили, какое число является решением уравнения.
Все эти соответствия имеют общее – во обоих случаях мы имеем два множества: в первом – это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором – это множество из трех уравнений и множество N натуральных чисел.
Связь (соответствие) между этими множества можно представить наглядно, при помощи графов.

Полученные множества показывают, что любое соответствие между двумя множествами Х и У можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары – это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
Определение. Соответствием между множествами Х и У называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами R, P, F, T и др.
2. Способы задания соответствий
Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества.
Пример. Соответствие между множествами Х = 1, 2, 4, 6 и У = 3, 5 можно задать: 1) при помощи предложения с двумя переменными: а в при условии, что а Х, в У; 2) перечислив пары чисел, принадлежащих подмножеству декартова произведения ХУ: (1,3),(1,5),(2,3),(2,5),(4,5). К этому способу задания относят также задание соответствия при помощи графа и графика.
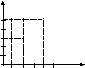
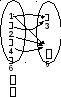
3. Соответствие обратное данному
Пример. Пусть S – соответствие «больше на 2» между множествами Х = 4, 5, 8, 10 и У = 2, 3, 6. Тогда S = (4,2), (5,3), (8,6) и его граф будет как на рисунке.
С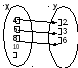
Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: х S у.
Определение. Пусть S – соответствие между множествами Х и У. Соответствие S -1 между множествами У и Х называется обратным данному, если у S -1 х тогда и только тогда, когда х S у. Соответствия S и S -1 называют взаимно обратными.
Выясним особенности их графиков. Построим график соответствия S = (4,2), (5,3), (8,6)
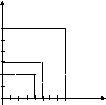
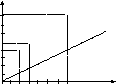
При построении графика соответствия S -1 = (2,4), (3,5), (6,8) мы должны первую компоненту выбирать из множества У = 2,3,6, а вторую – из множества Х = 4, 5, 8, 10. В результате график соответствия S -1 совпадет с графиком соответствия S. Чтобы различать графики соответствий S и S -1 , условились первую компоненту пары соответствия S -1 считать абсциссой, а вторую – ординатой. Например, если (5,3) S, то (3,5) S -1 . Точки с координатами (5,3) и (3,5), а в общем случае (х,у) и (у,х) симметричны относительно биссектрисы 1-го и 3-го координатных углов. Следовательно, графики взаимно обратных соответствий S и S -1 симметричны относительно биссектрисы 1-го и 3-го координатных углов.
Чтобы построить график соответствия S -1 , достаточно изобразить на координатной плоскости точки, симметричные точкам графика S относительно биссектрисы 1-го и 3-го координатных углов.
Источник
§8. Понятие соответствия между множествами. Способы задания соответствий
Пусть заданы два множества X и Y. Если для каждого элемента х Î Х указан элемент y Î Y, с которым сопоставляется х, то говорят, что между множествами X и Y установлено соответствие.
Иначе говоря, соответствием между элементами множеств X и Y называется любое подмножество G декартова произведения X ´ Y этих множеств. Если (х, у) Î G, то множество первых компонентов (D(G)) называется областью определения соответствия G, множество вторых компонентов (E(G)) –– областью значений этого соответствия.
Множество всех y Î Y, которые сопоставляются элементу х Î Х, называется образом х в Y. Множество же всех х Î Х, которым сопоставляют элемент y Î Y, называется прообразом y в Х.
Способы задания соответствия. Поскольку соответствие — это множество, то его можно задать теми же способами, что и любое множество: перечислением всех пар (х, у), где элементы х Î Х и y Î Y связаны данным соответствием; указанием характеристического свойства всех пар (х, у) элементов х Î Х, y Î Y, находящихся в рассматриваемом соответствии.
Когда множества X и Y конечные, то соответствие между элементами можно задать таблицей, где в левом столбце записывают элементы множества Х, а в верхней строке — элементы множества Y. Пары элементов, находящихся в соответствии G, будут находиться на пересечении соответствующих столбцов и строк.
Соответствие между двумя конечными множествами можно показать и при помощи графа. Множества X и Y показывают оваломи, элементы множеств X и Y обозначают точками, а стрелками соединяют соответствующие элементы так, что если имеет место (х, у) Î G, то стрелку проводят из точки х в точку у.
Когда множества Х и Y числовые, то можно построить график соответствия G на координатной плоскости.
Пример, график соответствия «меньше» между элементами множеств Х = <1, 3, 4, 6>и Y = <2, 5, 7>. Выпишем пары элементов, находящихся в данном соответствии: (1, 2), (1, 5), (1, 7), (3, 5), (3, 7), (4, 5), (4, 7), (6, 7). Если изобразить элементы множества Х на оси Ох, а элементы множества Y на оси Оу, а выписанные пары отметить точками на координатной плоскости, то получим график рассматриваемого соответствия между элементами множеств X и Y (рис. 13).
Источник
Лекция 8. Соответствия между элементами двух множеств. Определение соответствия между элементами двух множеств. Взаимно однозначные соответствия.
Соответствием между множествами Х и Y называется всякое подмножество произведения этих множеств.
Соответствие можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами Х = <2, 4, 6, 8>и Y = <3, 5, 7>можно задать:
1) при помощи предложения с двумя переменными: а -1 ( b ) элементов из Х таких, что ( х , b ) ∈ R: R -1 ( b ) = < х|( х , b ) ∈R >. Это множество называют полным прообразом элемента b при соответствии R.
Подмножество А⊂Х, состоящее из элементов х , имеющих образы в множестве Y, называют областью определения соответствия R. Подмножество В⊂Y, состоящее из элементов y , имеющих непустые прообразы в множестве Х, называют множеством значений соответствия R.
Пусть S – соответствие между множествами Х и Y. Соответствие S -1 между множествами Y и Х называется обратным данному, если у S -1 х тогда и только тогда, когда х S у .
Соответствия S и S -1 называют взаимно обратными . Граф соответствия S -1 получается из графа соответствия S изменением направления всех стрелок.

П р и м е р 1. Соответствие R между множествами X и Y задано при помощи графа (рис. 2). а) Укажите область отправления, область прибытия, область определения и множество значений соответствия R. б) Задайте это соответствие, перечислением пар чисел. в) Постройте график соответствия R в прямоугольной системе координат. г) Найдите соответствие R -1 , обратное данному, и постройте его график.
Р е ш е н и е. а) Из рисунка следует, что областью отправления данного соответствия R является множество Х = <1, 3, 5, 7>, а областью прибытия – множество Y = <0, 2, 4, 6>. Область определения образуют те числа из множества Х, от которых выходит хотя бы одна стрелка, т.е. А = <1, 3, 5>. В множество значений входят те элементы из множества Y, к которым идет хотя бы одна стрелка. Это множество В = <2, 4, 6>.
б) Каждая пара чисел, входящая в данное соответствие, на графе соединена стрелкой, поэтому в виде пар соответствие R можно записать так: <(1,2), (1,4), (3,2), (3,4), (3,6), (5,6)>.
в) График соответствия R в прямоугольной системе координат изображен на рис. 3.
г) Так как граф соответствия R -1 получается из графа соответствия R изменением направления стрелок, то соответствие R -1 можно получить из соответствия R, поменяв местами компоненты в парах: R -1 = <(2,1), (4,1), (2,3), (4,3), (6,3), (6,5)>. График обратного соответствия R -1 в прямоугольной системе координат изображен на рис. 4.
П р и м е р 2. Даны два множества: А = <-1, -2, -3, 1, 2, 3, 0>, N – множество натуральных чисел. Поставим в соответствие каждому числу а Î А его квадрат. Выпишите все пары, принадлежащие соответствию. Найдите образ элементов -2 и 0. Найдите полный прообраз 9.
Р е ш е н и е. Найдем множество пар, входящих в данное соответствие: <(-1, 1), (-2, 4), (-3,9), (1, 1), (2, 4), (3, 9)>. Пара (0, 0) в соответствии не присутствует, так как 0 не является натуральным числом. Образом элемента -2 будет число 4 (вторая компонента пары (-2, 4)), число 0 имеет пустой образ. Полным прообразом числа 9 будет множество <-3, 3>.
П р и м е р 3. Соответствие R задано с помощью пар (1, 2), (0, 0), (2, 4), (-1, -2), (-2, -4). Найдите область определения и множество значений этого соответствия. Какой формулой задается это соответствие?


Р е ш е н и е. В область определения Х входят первые компоненты пар соответствия, поэтому Х = <0, 1, 2, -1, -2>. Множество значений Y соответствия R составляют вторые компоненты пар соответствия, значит, Y = <0, 2, 4, -2, -4>. Замечаем, что вторая компонента в каждой паре получается из первой умножением на число 2, следовательно, данное соответствие можно задать с помощью формулы y = 2 x .
Задания для самостоятельной работы по теме 8:
1. Укажите соответствия, существующие между элементами множеств А и В, если: а) А – множество отрезков, В – множество чисел; б) А — множество треугольников, В – множество окружностей.
2. Даны два множества: А = <-1, -2, -3, 1, 2, 3, 0>, N – множество натуральных чисел. Поставим в соответствие каждому числу а∈А его квадрат. Выпишите все пары, принадлежащие соответствию. Найдите образ элементов -2 и 0. Найдите полный прообраз 9.
Источник





