Что называется картографической проекцией математический способ

Картографическая проекция

Картографи́ческая прое́кция — математически определенный способ отображения поверхности эллипсоида на плоскости.

Суть проекций связана с тем, что фигуру Земли — эллипсоид, не развертываемый в плоскость, заменяют на другую фигуру, развёртываемую на плоскость. При этом с эллипсоида на другую фигуру переносят сетку параллелей и меридианов. Вид этой сетки бывает разный в зависимости от того, какой фигурой заменяется эллипсоид.

Содержание

Искажения

В любой проекции существуют искажения, они бывают четырёх видов:

• искажения длин
• искажения углов
• искажения площадей
• искажения форм

На различных картах искажения могут быть различных размеров: на крупномасштабных они практически неощутимы, но на мелкомасштабных они бывают очень велики.

Искажения длин

Искажение длин — базовое искажение. Остальные искажения из него логически вытекают. Искажение длин означает непостоянство масштаба плоского изображения, что проявляется в изменении масштаба от точки к точке, и даже в одной и той же точке в зависимости от направления.

Это означает, что на карте присутствует 2 вида масштаба:

• Главный, он на карте подписывается, но на самом деле это масштаб исходного эллипсоида, развертыванием которого в плоскость карта и получена.

• Частный масштаб — их бесконечно много на карте, он меняется от точки к точке и даже в пределах одной точки.

Для наглядного изображения частных масштабов вводят Эллипс искажения.

Искажения площадей

Искажения площадей логически вытекают из искажения длин. За характеристику искажения площадей принимают отклонение площади эллипса искажений от исходной площади на эллипсоиде.

Искажения углов

Искажения углов логически вытекают из искажения длин. За характеристику искажений углов на карте принимают разность углов между направлениями на карте и соответствующими направлениями на поверхности эллипсоида .

Искажения формы

Искажения формы — графическое изображение вытянутости эллипсоида.

Классификация проекций по характеру искажений

Равноугольные проекции

Равноугольные проекции — проекции без искажений углов. Весьма удобны для решения навигационных задач. Масштаб зависит только от положения точки и не зависит от направления. Угол на местности всегда равен углу на карте, линия, прямая на местности — прямая на карте. Главным примером данной проекции является цилиндрическая Проекция Меркатора (1569 г.), которая и в наши дни используется для морских навигационных карт.

Равновеликие (равноплощадные) проекции

В равновеликих проекциях отсутствуют искажения площадей, но при этом сильны искажения углов и форм, (материки в высоких широтах сплющиваются). В такой проекции изображаются экономические, почвенные и другие мелкомасштабные карты.

Произвольные проекции

В произвольных проекциях имеются искажения и углов, и площадей, но в значительно меньшей степени, чем в равновеликих и равноугольных проекциях, поэтому они наиболее употребляемые.

Частным случаем произвольных проекций являются равнопромежуточные проекции, в которых сохраняются расстояния по некоторым выбранным направлениям: например, прямая азимутальная проекция, в которой правильно изображаются расстояния от полюса.

Классификация проекций по виду параллелей и меридианов нормальной сетки

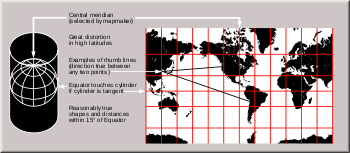
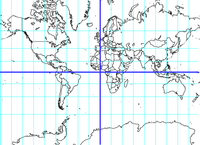
Цилиндрические проекции

В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг другу. Таким образом задается прямоугольная сетка цилиндрических проекций

Промежутки между параллелями пропорциональны разностям долгот. Промежутки между меридианами определяются принятым характером изображения или способом проектирования точек земной поверхности на боковую поверхность цилиндра. Из определения проекций следует, что их сетка меридианов и параллелей ортогональна. Цилиндрические проекции можно рассматривать как частный случай конических, когда вершина конуса в бесконечности.

По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и поперечные цилиндрические проекции в зависимости от расположения изображаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.

Существуют разные способы образования цилиндрических проекций. Наглядным представляется проектирование земной поверхности на боковую поверхность цилиндра, которая затем развертывается на плоскости. Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору, во втором — по двум стандартным параллелям, симметричным относительно экватора.

Цилиндрические проекции применяются при составлении карт мелких и крупных масштабов — от общегеографических до специальных. Так, например, аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равноугольных проекциях (на шаре).

В прямых цилиндрических проекциях одинаково изображаются одни и те же участки земной поверхности вдоль линии разреза — по восточной и западной рамкам карты (дублируемые участки карты) и обеспечивается удобство чтения по широтным поясам (например, на картах растительности, осадков) или по меридиональным зонам (например, на картах часовых поясов).

Косые цилиндрические проекции при широте полюса косой системы, близкой к полярным широтам, имеют географическую сетку, дающую представление о сферичности земного шара. С уменьшением широты полюса кривизна параллелей увеличивается, а их протяжение уменьшается, поэтому уменьшаются и искажения (эффект сферичности). В прямых проекциях полюс показывается прямой линией, по длине, равной экватору, но в некоторых из них (проекции Меркатора, Уэтча) полюс изобразить невозможно. Полюс представляется точкой в косых и поперечных проекциях. При ширине полосы до 4,5° можно использовать касательный цилиндр, при увеличении ширины полосы следует применять секущий цилиндр, то есть вводить редукционный коэффициент

Конические проекции

По характеру искажений конические проекции могут быть различными. Наибольшее распространение получили равноугольные и равнопромежуточные проекции. Образование конических проекций можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида).

В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий.

После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость. При проектировании по методу линейной перспективы получаются перспективные конические проекции, обладающие только промежуточными свойствами по характеру искажений.

В зависимости от размеров изображаемой территории в конических проекциях принимаются одна или две параллели, вдоль которых сохраняются длины без искажений. Одна параллель (касательная) принимается при небольшом протяжении по широте; две параллели (секущие) — при большом протяжении для уменьшения уклонений масштабов от единицы. В литературе их называют стандартными параллелями.

Азимутальные проекции

В азимутальных проекциях параллели изображаются концентрическими окружностями, а меридианы — пучком прямых, исходящих из центра

Углы между меридианами проекции равны соответствующим разностям долгот. Промежутки между параллелями определяются принятым характером изображения (равноугольным или другим) или способом проектирования точек земной поверхности на картинную плоскость. Нормальная сетка азимутальных проекций ортогональна. Их можно рассматривать как частный случай конических проекций.

Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.

В зависимости от искажений, азимутальные проекции подразделяются на равноугольные, равновеликие и с промежуточными свойствами. В проекции масштаб длин может сохраняться в точке или вдоль одной из параллелей (вдоль альмукантарата). В первом случае предполагается касательная картинная плоскость, во втором — секущая. В прямых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных — только для поверхности шара.

Азимутальную равновеликую проекцию называют также стереографической. Она получается проведением лучей из некоторой фиксированной точки поверхности Земли на плоскость, касательную к поверхности Земли в противолежащей точке.

Особый вид азимутальной проекции — гномоническая. Она получается проведением лучей из центра Земли к некоторой касательной к поверхности Земли плоскости. Гномоническая проекция не сохраняет ни площадей, ни углов, но зато на ней кратчайший путь между любыми двумя точками (то есть дуга большого круга) всегда изображается прямой линией; соответственно меридианы и экватор на ней изображаются прямыми линиями.

Псевдоконические проекции

В псевдоконических проекциях параллели изображаются дугами концентрических окружностей, один из меридианов, называемый средним — прямой линией, а остальные — кривыми, симметричными относительно среднего.

Примером псевдоконической проекции может служит равновеликая псевдоконическая проекция Бонна.

Псевдоцилиндрические проекции

В псевдоцилиндрических проекциях все параллели изображаются параллельными прямыми, средний меридиан — прямой линией, перпендикулярной параллелям, а остальные меридианы — кривыми. Причём средний меридиан является осью симметрии проекции.

Поликонические проекции

В поликонических проекциях экватор изображается прямой, а остальные параллели изображаются дугами эксцентрических окружностей. Меридианы изображаются кривыми, симметричными относительно центрального прямого меридиана, перпендикулярного экватору.

Кроме вышеперечисленных встречаются и другие проекции, не относящиеся к указанным видам.

Источник

Ура! География!

вторник, 9 ноября 2021 г.

8 класс
Тема: Картографические проекции. Искажения на картах.

Чтобы правильно изобразить земную поверхность на плоскости, необходимо провести математические расчёты и спроектировать геометрическую фигуру на плоскость, этот процесс называется картографической проекцией.

Картографическая проекция – математический способ перенесения земной поверхности на плоскость карты. Для построения картографической проекции используют вспомогательные геометрические фигуры: цилиндр, конус и плоскость. В зависимости от использования фигуры проекции могут быть цилиндрические, конические и азимутальные.

При составлении цилиндрической проекции используется цилиндр. Такую проекцию чаще всего используют для создания карт мира, материков и океанов, стран, находящихся в приэкваториальной зоне. При использовании такой проекции линии градусной сетки будут пересекаться под прямым углом, меридианы и параллели будут прямыми линиями.

Рис.1. Цилиндрическая проекция

При использовании конуса создается коническая проекция. В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели – дугами концентрических окружностей.

Азимутальную проекцию получают с помощью проектирования картографической сетки Земли на плоскость – касательную к полюсу Земли. Меридианы сетки на проекции имеют вид прямых, исходящих из центральной точки проекции, а параллели – концентрические окружности с центром на полюсе.

Поликоническими называют проекции, в которых проектирование сети параллелей и меридианов производится сразу на несколько конусов. Сетка: центральный меридиан и экватор – взаимно перпендикулярные прямые линии, остальные параллели – дуги эксцентрических окружностей, а меридианы – кривые линии (рис. 4). Используются при построении карт мира.

Условными называют проекции, при построении которых не прибегают к использованию вспомогательной геометрической поверхности. Сеть параллелей и меридианов строят исходя из каких-либо заданных условий. К условным проекциям принадлежат псевдоцилиндрические, псевдоконические, псевдоазимутальные и другие проекции, полученные путем преобразования исходных проекций.

Помимо упомянутых, существует много других типов и разновидностей картографических проекций. Проекцию, наиболее подходящую по характеру, величине и распределению искажений для той или иной карты, выбирают в зависимости от назначения, содержания карты, а также от размеров, конфигурации и географического положения поверхности картографируемой территории.

a — цилиндрическая, b — коническая, c — азимутальная, d — псевдоцилиндрическая,
e — псевдоконическая, f — поликоническая, g — псевдоазимутальная.

Различают проекции нормальные (ось цилиндра или конуса при проецировании совмещена с осью Земли), косые (наклон цилиндра или конуса относительно полярной оси составляет острый угол) и поперечные (угол между осью Земли и осью фигуры проекции составляет 90 градусов).

Поскольку наша планета является геоидом, ее поверхность невозможно перенести на плоскость без неточностей, поэтому все картографические проекции имеют искажения.

В зависимости от характера и размера искажений, проекции делятся на:

— равноугольные ( сохраняют углы и формы объектов, но искажают длины и площади) ;

— равновеликие ( сохраняют площади, но сильно изменяют углы и формы объектов) ;

— произвольные ( искажения длин, площадей и углов распределены на карте определенным образом ),

— равнопромежуточные (длины сохраняются либо по параллели, либо по меридиану).

Построенная на плоскости географическая сетка , изображающая меридианы и параллели, будет иметь определенные искажения, поэтому будут искажены изображения всех объектов земной поверхности. Характер и размеры искажений зависят от способа построения картографической сетки, на основе которой составляется карта.

Существуют различные виды картографических проекций. Каждому из них соответствуют определенная картографическая сетка и присущие ей искажения. В одном виде проекции искажаются размеры площадей, в другом — углы, в третьем — площади и углы. При этом во всех проекциях без исключения искажаются длины линий.

Выделяют четыре вида искажений на картах: длин, площадей, углов и форм объектов, они видны при сравнении градусной сетки на карте.

Признаки на карте

Одинаковые по длине расстояния на земной поверхности изображены на карте линиями разной длины

Длины равных по величине дуг меридианов на карте разные

Одноименные углы на земной поверхности и на карте разные

Углы между меридианами и параллелями не прямые

Форма географического объекта на земной поверхности и на карте разная

1. Отношение длины к ширине объекта на карте отличается от этого же отношения в натуре

2. Клетки сетки на одной широте разной формы

Объекты на земной поверхности с одинаковой площадью изображены на карте участками с разной площадью

Площади клеток картографической сетки на одной широте разные

Масштаб, указанный на картах, справедлив только на линиях и в точках нулевых искажений. Он называется главным. Во всех остальных частях карты масштаб отличается от главного и называется частным. Для его определения нужны специальные расчеты.

Судить о наличии на карте искажения длин удобно путем сравнения величины отрезков меридианов между соседними параллелями .

Если они повсеместно равны, то искажения длин по меридианам нет, если такого равенства нет (рис. отрезки АВ и CD ), то искажение длин линий имеется.

Если карта отображает такую большую территорию, что на ней показаны и экватор 0º и параллель 60° широты, то нетрудно по ней установить, имеется ли искажение длин вдоль параллелей. Для этого достаточно сравнить длину отрезков экватора и параллели с широтой 60° между соседними меридианами. Известно, что параллель 60° широты в два раза короче экватора. Если таково же соотношение указанных отрезков на карте, то искажения длин по параллелям нет; в противном случае оно имеется.

Искажения углов логически вытекают из искажения длин. За характеристику искажений углов на карте принимают разность углов между направлениями на карте и соответствующими направлениями на поверхности эллипсоида.
За показатель искажения углов между линиями картографической сетки принимают величину отклонения их от 90° и обозначают его греческой буквой ε (эпсилон).
ε = Ө – 90°,
где в Ө (тэта) – измеренный на карте угол между меридианом и параллелью.

На рисунке обозначено, что угол Ө равен 115°, следовательно, ε = 25°.
В точке, где угол пересечения меридиана и параллели остается на карте прямым, углы между другими направлениями могут быть измененными на карте, поскольку в каждой данной точке величина искажения углов может изменяться с переменой направления.

Простой способ выявления искаженности этого вида состоит в сравнении площадей клеток картографической сетки, ограниченных одноименными параллелями: при равенстве площадей клеток искажения нет. Это имеет место, в частности, на карте полушария, на которой заштрихованные клетки различаются по форме, но имеют одинаковую площадь.

Искажение форм состоит в том, что форма участка или занятой объектом территории на карте отлична от их формы на уровенной поверхности Земли. Наличие искажения этого вида на карте можно установить путем сопоставления формы клеток картографической сетки, расположенных на одной широте: если они одинаковы, то искажения нет.

— Проанализируйте физическую карту России, какие на ваш взгляд на ней существуют искажения?

— Сравните карту России и карту материков и океанов, найдите примеры искажения фигур и площадей.

Источник