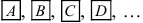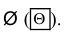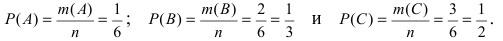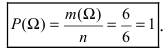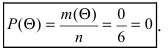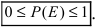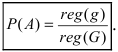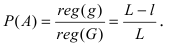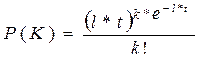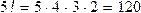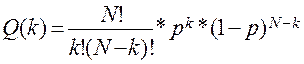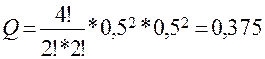Что есть способы определение вероятности

Определения вероятности событий — вычисление с примерами решения

Содержание:

Основные понятия теории вероятностей:

1. Предмет теории вероятностей.

Теория вероятностей — это математическая дисциплина, которая устанавливает взаимозависимость между случайными величинами в случайных массовых процессах. Одним из основных понятий в теории вероятностей является понятие случайного события.

Определение: Случайным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти.

Например, при подбрасывании монеты нельзя угадать заранее, что выпадет: “решка” (аверс) или “орел” (реверс). Каждое из этих событий является простым и не может быть выражено через более простые события.

Определение: Элементарным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти, а также не может быть представлено посредством более простых событий.

В теории вероятностей случайные элементарные события принято обозначать заглавными начальными буквами латинского алфавита

Определение: Сложным случайным событием называется событие, которое состоит из осуществления двух или более элементарных событий.

Определение: Эксперимент — это создание заранее заданного комплекса условий. Например, при подбрасывании монеты создают следующие условия: стол, на который падает монета, должен быть ровным, гладким, достаточно большим по площади, чтобы монета не могла скатиться.

Определение: Достоверным событием называется такое событие, которое обязательно произойдет в рамках данного опыта. Достоверное событие обозначается

Определение: Невозможным событием называется такое событие, которое ни при каких условиях не может произойти.

Невозможное событие обозначается

Например, совокупность выигрыша, проигрыша и ничья в шахматной партии образуют достоверное совокупное событие, т.е. одно из этих событий обязательно произойдет при игре в шахматы. При бросании кубика выпадение грани с 7 очками является невозможным событием.

Определение: Совместными событиями называются события, которые могут одновременно произойти в рамках данного опыта, все другие события называются несовместными.

Например, при бросании кубика выпадение грани с 4 очками (событие А) и выпадение четной грани (событие В) являются совместными событиями, а выпадение грани с 3 очками (событие А) и выпадение четной грани (событие В) являются несовместными событиями.

Определение: Полной группой случайных событий называется совокупность таких несовместных событий, что в результате проведения эксперимента хотя бы одно из них обязательно произойдет.

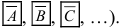
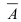
Определение: Противоположными событиями называются такие несовместные события, которые образуют полную группу (обозначаются Например, если событие А состоит в попадании снаряда в цель, то событие состоит в том, что снаряд не попадет в цель.

Замечание: Если в словесном описании случайного события присутствуют слова “хотя бы один”, то такое событие противоположно событию, содержащему в своем словесном описании слова “ни один”.

Определение: Равновозможными событиями называются такие случайные события, которые в условиях эксперимента имеют объективно равные шансы не произойти или произойти.

Например, однородность материала кости и несмещенность центра тяжести кубика являются теми условиями, при которых объективно возможно выпадение любой грани кубика.

Способы определения вероятности событий

Существуют два способа определения вероятности события

1. Теоретический способ основан на непосредственном (без проведения специального эксперимента) определении вероятности события по формуле: P(A)=m/n.
2. Статистический способ основан на предварительном прове­дении большого числа испытаний. При этом подсчитывают вероят­ность по формуле: h (A) = k / L.

Классическое определение вероятности

Определение: Вероятностью события называется численная мера степени объективной возможности случайного события.

Классическое определение вероятности применяется для нахождения вероятности конечного числа несовместных и равновозможных событии, образующих полную группу.

Пример №1

Пусть в урне находится 6 шаров: 1 белый, 2 красных и 3 синих. Опыт состоит в том, что из урны наудачу извлекают один шар. Определить полную группу случайных событий и наиболее вероятное событие.

Решение:

Для данного опыта полная группа событий состоит из 6 равновозможных исходов. Обозначим через А событие, состоящее в том, что из урны извлекают белый шар; В — красный шар; С — синий шар. Очевидно, событие С является более объективно возможным событием, чем события А и В, так как синих шаров в урне больше, чем белых и красных.

Классическое определение вероятности состоит в следующем:

Определение: Вероятностью случайного элементарного события называется отношение числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу.

В Примере число исходов, благоприятствующих извлечению белого шара, равно m(А) = 1, красного шара — m(В) = 2 и синего шара — m(С) = 3. Общее число всех равновозможных, несовместных, элементарных исходов, образующих полную группу, равно числу шаров в урне, т.е. n = 6. Таким образом, вероятности извлечь из урны тот или иной шар равны отношению числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу:

В силу того,что события А, В и С образуют достоверное совокупное событие, то 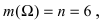следовательно, вероятность достоверного события равна:

Если в рассматриваемом Примере. обозначить через D событие, состоящее в том, что из урны извлекают черный шар, то этому событию благоприятствует нуль исходов (m(D) = 0), так как в урне нет черных шаров. Следовательно, событие D является невозможным событием О, а его вероятность равна:

Из рассмотренного Примере. видно, что вероятности всех событий есть положительные величины, которые принимают значения между вероятностью невозможного (0) и вероятностью достоверного (1) событий, т.е.

Замечание: Вероятность любого случайного события есть безразмерная и положительная величина, принимающая значения из промежутка от 0 до 1. Чем ближе вероятность события к нулю, тем меньше его возможность появления в данном опыте. Чем ближе вероятность события к единице, тем выше его возможность появления в данном эксперименте.

Геометрический способ определения вероятности

Геометрическое определение вероятности применяется для вычисления вероятности бесконечного числа несовместных и равновозможных событий, образующих полную группу.

Пусть имеется некоторая область G, которая может быть представлена в виде линии, площади или объема. Внутри области G находится другая область g, внутрь которой должна попасть точка, наудачу брошенная в область G. Пусть событие А состоит в том, что при попадании в область g включается лампочка, а при попадании в область G лампочка не загорается. Обозначим размеры областей g и G через 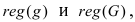соответственно. Появлению события А благоприятствует размер области g, а размер области G определяет общее число возможных исходов, следовательно, вероятность появления события А равна

Пример №2

Пусть на нити длиной L подвешен груз. Определить вероятность разрыва нити в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l.

Решение:

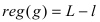
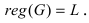
Пусть событие А состоит в том, что нить разорвется в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l. Появлению этого события благоприятствуют все точки нити длиной L-l, т.е. , а длина всей нити равна L, т.е. Согласно геометрическому определению вероятности вероятность появления события А равна

Статистический способ определения вероятности событий

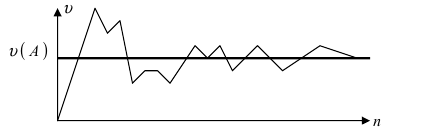
Данный способ определения вероятности событий применяется тогда, когда неприменимы два вышеприведенных способа. В основу данного способа положена устойчивость частоты появления изучаемого события при достаточно большом числе проводимых опытов, т.е. P(A) = v(A). При небольшом числе испытаний частота носит случайный характер, но при 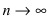она стабилизируется возле некоторого положения, характеризующего связь между комплексом условий и наблюдаемым событием (Рис. 1).

Рис. 1. Стабилизация частоты появления случайного события при

Косвенный способ определения вероятности событий

Данный способ определения вероятности событий применяется тогда, когда неприменимы три вышеприведенных способа. Он основан на теоремах теории вероятностей, которые рассматриваются ниже.

Рекомендую подробно изучить предметы:

Теория вероятностей Математическая статистика

Ещё лекции с примерами решения и объяснением:

• Предельные теоремы теории вероятностей
• Точечные оценки, свойства оценок
• Доверительный интервал для вероятности события
• Проверка гипотезы о равенстве вероятностей
• Многомерные случайные величины
• Случайные события — определение и вычисление
• Системы случайных величин
• Вероятность и риск

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Способы определения вероятностей

Существуют два способа определения вероятности события.

1. Теоретический способ основан на непосредственном (без проведения специального эксперимента) определении вероятности события по формуле:

где m — число случаев, благоприятствующих наступлению события А; n — число всех равновозможных случаев из полной группы несов­местных событий.

Например, априори известно, что при одном выстреле в мишень равновероятно можно получить 0, 1, 2. 10 очков. Какова вероят­ность того, что в результате одного выстрела будет получено 7 очков?

P(A) = m/n = 1/11= 0,091.

2. Статистический способ основан на предварительном прове­дении большого числа испытаний. При этом подсчитывают вероят­ность по формуле:

где k — число появления события А, называемое частостью А; L — общее число событий, наступивших в некоторой серии испытаний при определенном неизменном комплексе условий; h (A) — статисти­ческая вероятность события.

При большом числе испытаний значение частоты h (A) стабили­зируется и приближается к величине вероятности Р(A). Следует подчеркнуть, что статистическую вероятность события можно использовать в качестве значения вероятности только при большом числе испытаний.

В теории вероятностей существует большое количество математических соотношений, используемых на практике. Основные из них описывают сложение или умножение вероятностей.

Вероятность наступления ряда из m событий, принадлежащих к множеству несовместных N событий (N>m), равна сумме вероятностей этих событий:

Отсюда, в частности, следует, что сумма вероятностей собы­тий, образующих полную группу, равна 1; сумма вероятностей двух противоположных событий равна 0.

Например, известно, что экзаменационные оценки, полученные слушателями, распределились следующим образом: 4% слушателей по­лучили «2», 6 — «3», 60 — «4» и остальные 30% слушателей — «5». Какова вероятность, что указанный наугад слушатель этой группы получил отрицательную оценку?

Какова вероятность, что указанный наугад слушатель получил положительную оценку?

P(З,4,5) = P(3) + P(4) + P(5) =6%/100% + 60%/100% + 30%/100% = 0,06 + 0,6 + 0,3 = 0,96.

Вероятность одновременного наступления нескольких независи­мых событий равна произведению вероятностей этих событий:

P(C) = P(A1*A2*. *Ak) = P(A1)*P(A2)*. *P(Ak).

Два стрелка одновременно стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка (Р1) = 0,8, а для второго (Р2) = 0,6. Как найти вероятность того, что оба стрелка попадут в мишень?

Р = Р1* Р2 = 0,8 * 0,6 = 0,48.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности по­явления их совместного события:

P(C) = P(A+B) = P(A) + P(B) — P(A) * P(B)

Две поисковые группы участвуют в обнаружении преступника в лесном массиве. Вероятность обнаружения преступника первой груп­пой (Р1) = 0,8; второй группой (Р2) = 0,4. Какова вероятность того, что преступника обнаружит хотя бы одна группа?

Р = Р1 + Р2 — Р1 * Р2 = 0,8 + 0,4 — 0,32 = 0,88.

Математические соотношения теории вероятностей позволяют по вероятностям одних случайных событий находить вероятности других случайных событий, связанных с ними. Например, вероят­ность какого-либо события В, вычисленная в предположении, что перед этим наступило связанное с ним событие А, называется практические приложения соотношения условной вероятности можно проиллюстрировать следующими примерами.

При медицинском освидетельствовании лиц, претендующих на получение разрешения на вождение автомобиля, оказалось, что из N (общего числа претендентов) Na страдают дальтонизмом, Nb — женщины. Пусть А и В означают события, состоящие соответственно в том, что случайно выбранное лицо страдает дальтонизмом или яв­ляется женщиной. В частности, может оказаться необходимым найти вероятность того, что случайно выбранная женщина страдает даль­тонизмом, т.е. найти:

где: Р(А/В) — вероятность события А (дальтонизм) при условии, что произошло событие В (выбрана женщина); Р(AВ) — вероятность того, что женщина страдает дальтонизмом; Р(В) — вероятность то­го, что случайно выбранное лицо из N — женщина.

Так, при N = 240 и Nb = 30; Р(В) = Nb/N = 0,125. По дан­ным генетических исследований известно, что для женщин Р(АВ) = 0,0001. Таким образом, Р(А/В) = 0,0001/0,125 = 0,0008.

Следует отметить, что если Р(В/А) = Р(В) и Р(А/В) = Р(А), то события В и А взаимонезависимы.

Наряду со случайными событиями в теории вероятностей и ее применениях рассматриваются случайные величины. Представим себе, что при каждом наблюдении некоторая величина принимает какое-то значение в зависимости от случая. Например, количество звонков в дежурную часть по линии «02» за 1 час.

Случайные величины различаются как теми значениями, которые они способны принимать, так и вероятностями, с которыми эти значения принимаются. Например, вероятность того, что за промежуток времени t число вызовов патрульного наряда окажется равным k. Как показывают многочисленные наблюдения такая вероятность согласуется с формулой:

где l — некоторая положительная постоянная.

,а k! – факториал, причем n!= n(n — 1)(n — 2). ×3×2×1, пример:

Эта формула получила название формулы Пуассона. Скорость молекулы газа также случайна и может принимать любые значения. Этих значений столько же, сколько положительных чисел. Как в этом случае задавать вероятности этих значений? Математики пошли по такому пути: стали определять не вероятность каждого из возможных значений, а вероятность того, что случайная величина x примет значение меньшее, чем заданное значение.

позволяющее по функции распределения определять вероятность выполнения указанного неравенства.

К более сложным соотношениям теории вероятностей относятся формулы Бернулли и Пуассона.

Формула Бернулли, описывающая вероятность того, что в N не­зависимых испытаниях, в каждом из которых вероятность появления события p (0 £ p £ 1), событие наступит k раз (безраз­лично — в какой последовательности), равна:

Например, состязаются два равносильных самбиста. Какова ве­роятность для одного из них выиграть две схватки из четырех?

Вероятность выигрыша p = 0,5, так как соревнуются два равных самбиста, и вероятность проигрыша 1-p = 0,5, тогда

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник