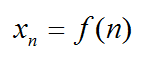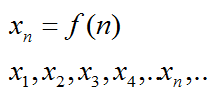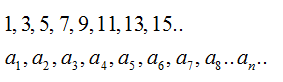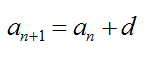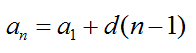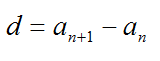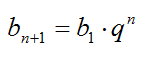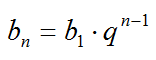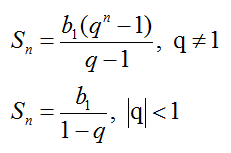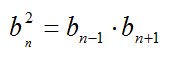Числовые последовательности способы задания числовых последовательностей предел последовательности

Числовые последовательности для чайников: определение, формулы

• 12 января 2021 г.
• 10 минут
• 78 883
• 2

По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.

Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность?

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Какие бывают последовательности

• постоянную, или монотонную последовательность: 1, 1, 1, 1, 1.
• возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
• убывающую последовательность, в которой каждый следующий элемент меньше предыдущего

Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.

Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Посмотрим на числа:

Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.

Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:

Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.

Сумма первых n членов прогрессии вычисляется по формуле:

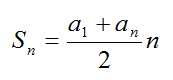
Также африфметическая прогрессия обладает характреристическим свойством:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:

Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:

Сумма первых n членов прогрессии:

Характеристическое свойство геометрической прогрессии:

Способы задания последовательностей

Последовательность можно задать несколькими способами:

1. Аналитически или, проще говоря, формулой.
2. Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
3. Описательно, простым перечислением всех элементов последовательности.

Предел последовательности

Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.

Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.

Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.

Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел.

Что нужно помнить, вычисляя пределы последовательностей

Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.

1. Последовательность может иметь только один предел.
2. Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
3. Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
4. Предел постоянной последовательности равен ее постоянному.
5. Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
6. Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
7. Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
8. Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей.
9. Постоянный множитель можно выносить за знак предела.
10. Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором.

Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.

Источник

Теоретический материал по теме: Последовательности. Способы задания и свойства числовых последовательностей. Понятие о пределе последовательности.

Тема: Последовательности. Способы задания и свойства числовых последовательностей. Понятие о пределе последовательности.

Цели: создание благоприятных условий для изучения понятия числовой последовательности; ввести определение предела последовательности и предела функции; познакомить с правилами вычисления пределов функции в точке и на бесконечности.

Определение№1: множество чисел, каждое из которых снабжено своим номером, называется числовой последовательностью.

Числовая последовательность представляет собой не что иное, как множество нумерованных чисел, упорядоченных наподобие натурального ряда, т.е. располагаемое в порядке возрастания номеров. Последовательность может содержать как конечное, так и бесконечное число членов.

Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, — бесконечной последовательностью.

Иногда бесконечную числовую последовательность вводят, используя понятие функции:

Определение №2: Функцию у = f ( x ), xN называют функцией натурального аргумента или числовой последовательностью и обозначают: у = f ( n ), или у₁, у₂, у₃. у _n или у( n ).

Последовательности можно задавать различными способами, например, словесно, когда правило задавания последовательности описано словами, без указания формулы. Так, словесно задается последовательность простых чисел:

Особенно важны аналитический и рекуррентный способы задания последовательности.

Говорят, что последовательность задана аналитически, если указана формула ее n -го члена.

Приведем три примера.

у _n = n 2 . Это аналитическое задание последовательности

Указав конкретное значение n , нетрудно найти член последовательности с соответствующим номером. Если. Например, n = 9, то у₉ = 9 2 = 81, если

у _n = С. Здесь речь идет о последовательности С, С, С, …., С, …. . Такую последовательность называют постоянной (или стационарной).

у _n = 2 n . Это аналитическое задание последовательности 2, 2 2 , 2 3 , ….,2 n , …

Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее вычислить n — й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия – это числовая последовательность (а _n ), заданная рекуррентно соотношениями:

(а и d – заданные числа, d – разность арифметической прогрессии)

Геометрическая прогрессия – это числовая последовательность ( b _n )? Заданная рекуррентно соотношениями:

( b и q – заданные числа, b ≠0, q ≠ 0; q знаменатель геометрической прогресси прогрессии).

Пример: Выписать первые пять членов последовательности, заданной рекуррентно:у₁ =1; у₂ = 1; у _n = у _{n -2} + у _{n -1}

Решение. n –й член последовательности равен сумме двух предшествующих ему членов. Значит, последовательно получаем:

Последовательность (х _n ) называется ограниченной, если существуют такие два числа m и М, что для всех n N выполняется неравенство m ≤ х _n ≤М.

Последовательность (х _n ) называется ограниченной сверху, если существует такое число М, что для всех n N выполняется неравенство х _n ≤М.

Последовательность (х _n ) называется ограниченной снизу, если существует такое число m , что для всех n N выполняется неравенство m ≤ х _n

Например: последовательность (х _n ), заданная формулой общего члена х _n = n , ограничена снизу (например, число 0) и не ограничена сверху.

Последовательность (х _n ) называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т.е. если для любого натурального n выполняется неравенство х _{n +1} > х _{n .}

Последовательность (х _n ) называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, т.е. если для любого натурального n выполняется неравенство х _{n +1} n _.

Последовательность (х _n ) называется невозрастающей, если каждый ее член, начиная со второго, не более предыдущего, т.е. если для любого натурального n выполняется неравенство х _{n +1} ≤ х _{n .}

Последовательность (х _n ) называется неубывающей, если каждый ее член, начиная со второго, не меньше предыдущего, т.е. если для любого натурального n выполняется неравенство х _{n +1} ≥ х _{n .}

Возрастающие, убывающие, невозрастающие и неубывающие последовательности образуют класс монотонных последовательностей.

Предел числовой последовательности.

Рассмотрим для числовые последовательности – (у _n ) и ( x _n ).

( x _n ): 1,

Изобразим члены этих последовательностей точками на координатной прямой.

0 1 3 5 7 9 11 у

Замечаем, что члены последовательности ( x _n ) как бы «сгущаются» около точки 0 – говорят последовательность сходятся , а у последовательности (у _n ) такой точки сгущения нет – и говорят, что последовательность расходится.

Математики не используют термин точка сгущения, а они говорят предел последовательности.

Определение: Число b называется пределом последовательности (у _n ), если в любой заранее выбранной окрестности точки b содержится все члены последовательности, начиная с некоторого номера.

Пишут так: у _n → b или читают так: предел последовательности у _n при стремлении n к бесконечности равен b .

На практике используется еще одно истолкование равенства , связанное с приближенными вычислениями: если последовательность у _n = f ( _n ) сходится к числу b , то выполняется приближенное равенство f ( _n )≈ b , причем это приближенное равенство тем точнее, чем больше n .

Необходимое условие сходимости произвольной числовой последовательности:

Для того чтобы последовательность сходилась, необходимо, чтобы она была ограниченной.

Достаточное условие сходимости последовательности.

Если последовательность монотонна и ограничена, то она сходится. (теорема К.Вейерштрасса)

Свойства сходящихся последовательностей

Если последовательность сходится, то только к одному пределу.

Если последовательность сходится, то она ограничена.

Если последовательность монотонна и ограничена, то она сходится.

Если , то последовательность у _n = q n расходится.

Теоремы о пределах последовательностей.

Если

Если , то

Для любого натурального показателя m и любого коэффициента k справедливо соотношение:

Предел суммы равен сумме пределов:

Предел произведения равен произведению пределов:

Предел частного равен частному пределов: , где с≠0.

Постоянный множитель можно выносить за знак предела:

Нахождение пределов последовательности:

Найти предел последовательности:

а) х _n = б) х _n = в)

Решение: а) применив правило «предел произведения», получим:

б) применим правило «предел суммы» и получим:

в) в подобных случаях применяют искусственный прием: делят числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n . В данном примере разделим числитель и знаменатель дроби почленно на n 2 . Имеем: (здесь мы применили правило «предел дроби»).

Пределы функций. Нахождение пределов функции в точке и на бесконечности.

Теория пределов позволяет определить характер поведения функции у = f ( x ) при заданном изменении аргумента.

Пусть функция f (х) определена в некоторой окрестности точки х =х ₀ , за исключением, быть может, самой точки х ₀ .

Число А называется пределом функции f (х) в точке х ₀ , если для любого числа >0 найдется такое положительное число , что для любого х х ₀ , удовлетворяющего неравенству | х — хо | , выполня ется соотношение | f ( x ) — А |

То, что функция f ( x ) в точке х ₀ имеет предел, равный А, обозна чают следующим образом:

Геометрически существование данного предела означает, что каково бы ни было >0, найдется такое число , что для всех х, заключенных между х ₀ + , и х ₀ — (кроме, быть может, самой точки х _с ), график функции у = f ( x ) лежит в полосе, ограниченной прямыми у = А + и у = А- (рис.1)

Таким образом, понятие предела функции дает возможность от ветить на вопрос, к чему стремятся значения функции, когда значе ния аргумента стремятся к х ₀

Число А называют пределом функции f ( x ) при х, стремящимся к х ₀ , если разность f ( x ) — А по абсолютной величине есть величина бесконечно малая.

Практическое приложение темы «Предел функции в точке».

а) б) в) г) д);

2. Вычислите пределы следующих функций:

а)

б)

в).

3. Используя разложение на множители преобразовать дроби и вычислить предел функции в точке:

а) б) в) г) д)

е) ;

ж) ;

з).

4. Найти предел функции в точке, используя способ избавления знаменателя(числителя) от иррациональности (помножить на сопряженное выражение):
а) ; б) ; в) .

Вопросы для самоконтроля .

Сформулируйте определение предела функции в точке.

Повторите основные теоремы о пределах.

Повторите способы преобразования дробных выражений, используя материалы практических занятий, справочную литературу.

Вычислите пределы функции в точке:

а) ; в) ;

б) ; г) .

а) ; б) ; в) ; г) ; д).

а);

а) .

Дайте определение числовой последовательности.

Перечислите способы задания последовательностей.

Какие последовательности называют ограниченными?

Сформулируйте определение предела числовой последовательности.

Сформулируйте необходимые условия сходимости последовательности.

Сформулируйте достаточные условия сходимости последовательности

Дайте определение предела функции в точке.

Перечислите основные теоремы о пределах функции в точке.

Источник