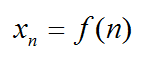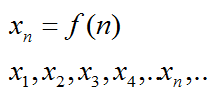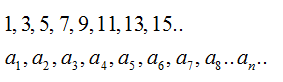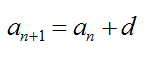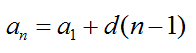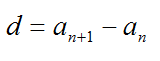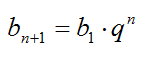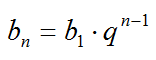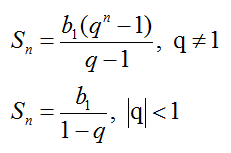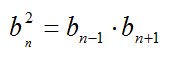Числовая последовательность понятие способы задания свойства предел числовой последовательности

Числовые последовательности для чайников: определение, формулы

• 12 января 2021 г.
• 10 минут
• 79 198
• 2

По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.

Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность?

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Какие бывают последовательности

• постоянную, или монотонную последовательность: 1, 1, 1, 1, 1.
• возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
• убывающую последовательность, в которой каждый следующий элемент меньше предыдущего

Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.

Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Посмотрим на числа:

Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.

Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:

Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.

Сумма первых n членов прогрессии вычисляется по формуле:

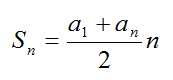
Также африфметическая прогрессия обладает характреристическим свойством:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:

Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:

Сумма первых n членов прогрессии:

Характеристическое свойство геометрической прогрессии:

Способы задания последовательностей

Последовательность можно задать несколькими способами:

1. Аналитически или, проще говоря, формулой.
2. Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
3. Описательно, простым перечислением всех элементов последовательности.

Предел последовательности

Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.

Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.

Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.

Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел.

Что нужно помнить, вычисляя пределы последовательностей

Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.

1. Последовательность может иметь только один предел.
2. Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
3. Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
4. Предел постоянной последовательности равен ее постоянному.
5. Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
6. Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
7. Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
8. Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей.
9. Постоянный множитель можно выносить за знак предела.
10. Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором.

Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.

Источник

Электронный конспект для обучающихся «Числовые последовательности. Предел числовой последовательности»

Последовательности. Способы задания и свойства числовых последовательностей. Предел последовательности.

Последовательность – ряд чисел

Каждое число имеет свой номер (первое, второе и т.д.)

218; 220; 218; 220;…..

Числовая последовательность — множество нумерованных чисел, располагаемое в порядке возрастания номеров.

Последовательность может быть конечной или бесконечной

Определение: Функцию у = f ( x ), xN называют функцией натурального аргумента или числовой последовательностью и обозначают: у = f ( n ), или у₁, у₂, у₃. у _n или у( n ) или а1 , а2,…, а n … или а( n ).

Способы задания последовательностей.

Словесно (описание словами, без указания формулы)

Аналитический способ (формулой)

Рекуррентный способ задания последовательности.

Приведем три примера.

у _n = n 2 — аналитическое задание последовательности

1,4,9,16,…, n 2 , …, где n – номер элемента последовательности

у _n = С — последовательность С, С, С, …., С, …. . Такую последовательность называют постоянной (или стационарной).

Рекуррентный способ задания последовательности — указывается правило, позволяющее вычислить последующий элемент последовательности, если известны предыдущие.

№ 1. Вычислите у1, у2, у3, у4, у5 и запишите в виде ряда чисел:

А)

Б)

В)

А)

Б)

Предел числовой последовательности

Рассмотрим числовую последовательность (у _n )

(у _n ) =

Изобразим элементы этой последовательностей точками на координатной прямой.

0 0,125 0,25 0,5 1

все числа последовательности (у _n ) «сгущаются» около точки 0

– последовательность сходится к числу 0 .

«точка сгущения» ≡ предел последовательности

Определение: Число b называется пределом последовательности (у _n ), если в любой заранее выбранной окрестности точки b содержится все элементы последовательности, начиная с некоторого номера.

у _n → b или

читают так: предел последовательности у _n при стремлении n к бесконечности равен b .

Необходимое условие сходимости произвольной числовой последовательности:

Для того чтобы последовательность сходилась, необходимо, чтобы она была ограниченной.

Достаточное условие сходимости последовательности.

Если последовательность монотонна и ограничена, то она сходится.

(0 q ≤ 1)

Если , то:

Предел суммы равен сумме пределов:

Предел произведения равен произведению пределов:

Предел частного равен частному пределов: , где с≠0.

Постоянный множитель можно выносить за знак предела:

Найти предел последовательности:

а) х _n =

б) х _n =

Решение: применим правило «предел суммы»:

0 – 0 + 3 = 3

в)

в подобных случаях применяется искусственный прием:

Деление числителя и знаменателя дроби (каждого слагаемого ) на наивысшую из имеющихся степень переменной n .

В данном примере разделим числитель и знаменатель дроби на n 2 (каждое слагаемое):

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 801 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 283 человека из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-400096

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В российских школах оборудуют кабинеты для сообщества «Большой перемены»

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Минпросвещения работает над единым подходом к профилактике девиантного поведения детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник