Числовая функция способы задания график функции свойства функций

Источник

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Лекция по математике «Числовая функция, ее свойства и графики».

Тема: Числовые функции, их свойства и графики

Тип урока: урок-лекция.

Целевая аудитория : обучающиеся 1 курса специальностей СПО 151031, 190631.

образовательные : систематизировать имеющиеся знания в области числовых функций и их свойств, научиться исследовать графики функций по их свойствам.

развивающие : формировать умения анализировать свойства функций на основе имеющихся знаний, формировать аналитическое мышление, развивать навыки по применению знаний в различных ситуациях.

воспитательные : формировать культуру умственного труда, создавать для каждого ученика ситуацию успеха, развивать коммуникативные умения; формировать положительную мотивацию к учению; развивать умение говорить и слушать других.

Метод обучения : объяснительно-иллюстративный.

Формы обучения : фронтальная, индивидуальная.

Оборудование : доска, проектор, экран. (Лекция построена исходя из реальных возможностей учебного кабинета. При наличии интерактивной доски необходимо работу с графиками проводить с ее помощью).

Приложение: презентация «Свойства числовой функции».

1. Организационный этап.

Приветствие, проверка присутствия на уроке, целеполагание.

2. Изложение теоретического материала

Определение : Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.

Обозначение: y = f(x),

где x – независимая переменная (аргумент), y – зависимая переменная (функция). Множество значений x называется областью определения функции (обозначается D(f)). Множество значений y называется областью значений функции (обозначается E(f)). Графиком функции называется множество точек плоскости с координатами (x, f(x))

Способы задания функции.

аналитический способ (с помощью математической формулы);

табличный способ (с помощью таблицы);

описательный способ (с помощью словесного описания);

графический способ (с помощью графика).

Основные свойства функции.

1. Четность и нечетность

Функция называется четной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = f(x)

График четной функции симметричен относительно оси 0y

Функция называется нечетной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = –f(x)

График нечетной функции симметричен относительно начала координат.

Функция f(x) называется периодической с периодом , если для любого х из области определения f(x) = f(x+Т) = f(x-Т) .

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x ₁ и x ₂ из этого множества, таких, что x _{1 2} выполнено неравенство f(x ₁ ) ₂ ).

Функция f(x) убывает на множестве Р , если для любых x ₁ и x ₂ из этого множества, таких, что x _{1 2} выполнено неравенство f(x ₁ ) > f(x ₂ ).

функция возрастает, если большему значению аргумента соответствует большее значение функции;

функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Точка Х _max называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Х _max , выполнено неравенство f(х) f(X _max ).

Значение Y _max =f(X _max ) называется максимумом этой функции.

Х _max – точка максимума

Точка Х _min называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Х _min , выполнено неравенство f(х) f(X _min ).

Значение Y _min =f(X _min ) называется минимумом этой функции.

X _min – точка минимума

X _min , Х _max – точки экстремума

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

Нулём функции y=f(x) называется такое значение аргумента x ₀ , при котором функция обращается в нуль.

Линейная функция y=kx+m

Графиком функции y=kx+m является прямая .

Свойства функции y=kx+m

2) возрастает, если k>0, убывает, если k

3) не ограничена ни снизу, ни сверху;

4) нет ни наибольшего, ни наименьшего значений;

5) функция непрерывна

Функция y=kx 2 ,k≠0

Графиком функции y=kx 2 ,k≠0 является парабола с вершиной в начале координат и с ветвями, направленными вверх, если k>0, и вниз, если k

Свойства функции y=kx 2 ,k≠0

2) убывает на луче (−∞;0], возрастает на луче [0;+∞);

3) ограничена снизу, не ограничена сверху;

4) y _наим =0, наибольшего не существует;

5) функция непрерывна;

Свойства функции y=kx 2 ,k≠0

2) возрастает на луче (−∞;0], убывает на луче [0;+∞);

3) не ограничена снизу, ограничена сверху;

4) наименьшего значения не существует, y _наиб =0;

5) функция непрерывна;

7) выпукла вверх.

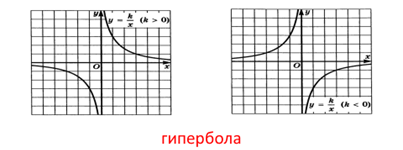
Графиком функции является гипербола .

Свойства функции y=k/x

2) если k>0, то функция убывает на открытом луче (−∞;0) и на открытом луче (0;+∞); если k

3) не ограничена ни снизу, ни сверху;

4) нет ни наибольшего, ни наименьшего значений;

5) функция непрерывна на открытом луче (−∞;0) и на открытом луче (0;+∞);

Графиком функции y=√x является ветвь параболы .

Свойства функции y=√x

3) ограничена снизу, не ограничена сверху;

4)y наим =0, наибольшего не существует;

5) функция непрерывна;

7) выпукла вверх.

Графиком функции является объединение двух лучей : y=x,x≥0 и y= −x, x≤0.

Свойства функции y=|x|

2) убывает на луче (−∞;0], возрастает на луче [0;+∞);

3) ограничена снизу, не ограничена сверху;

4) y _наим =0, наибольшего не существует;

5) функция непрерывна;

Функция y=ax 2 +bx+c

Графиком функции y=ax 2 +bx+c является парабола с вершиной в точке (x ₀ ;y ₀ ), где x ₀ =−b/2a,y ₀ =f(x ₀ )=ax ₀ 2 +bx ₀ +c, и с ветвями направленными вверх, если a>0, и вниз, если a

Свойства функции y=ax 2 +bx+c

2) убывает на луче (−∞;−b/2a], возрастает на луче [−b/2a;+∞);

3) ограничена снизу, не ограничена сверху;

4) y _наим =y0, наибольшего не существует;

5) функция непрерывна;

2) возрастает на луче (−∞;−b/2a], убывает на луче [−b/2a;+∞);

3) не ограничена снизу, ограничена сверху;

4) наименьшего значения не существует, y наиб =y0;

5) функция непрерывна;

7) выпукла вверх.

3. Подведение итогов учебного занятия.

1. Что такое числовая функция?

2. Назовите способы ее задания.

3. Назовите основные свойства числовой функции.

4. Перечислите элементарные функции, изученные на уроке.

4. Домашнее задание.

Пользуясь теоретическим материалом лекции (основными свойствами функции), выполнить следующее:

1) построить графики функций: а) y =3 x 2 б) y =-5/ x

2) Записать их свойства, используя построенные графики.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 832 человека из 77 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 298 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 609 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

Разработка урока-лекции по теме «Числовые функции их свойства и графики» с презентацией. Урок проводится на первом курсе технических специальностей среднего профессионального образования.

· образовательные : систематизировать имеющиеся знания в области числовых функций и их свойств, научиться исследовать графики функций по их свойствам.

· развивающие : формировать умения анализировать свойства функций на основе имеющихся знаний, формировать аналитическое мышление, развивать навыки по применению знаний в различных ситуациях.

· воспитательные : формировать культуру умственного труда, создавать для каждого ученика ситуацию успеха, развивать коммуникативные умения; формировать положительную мотивацию к учению; развивать умение говорить и слушать других.

Метод обучения : объяснительно-иллюстративный.

Формы обучения : фронтальная, индивидуальная.

Оборудование : доска, проектор, экран. (Лекция построена исходя из реальных возможностей учебного кабинета. При наличии интерактивной доски необходимо работу с графиками проводить с ее помощью).

Номер материала: 317617

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Пензенские родители смогут попасть в школы и детсады только по QR-коду

Время чтения: 1 минута

Студентам вузов могут разрешить проходить практику у ИП

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник