Сколькими способами можна распределить 12 классных комнат под 12 учебных кабинетов? С подробным описанием.
Задача о покрытии конечного множества системой его подмножеств (12 из 12)
Пусть имеем некоторое множество и систему его подмножеств. Требуется найти минимальное количество подмножеств, покрывающих исходное множество. Задачу можно представить с помощью двудольного графа: к первой доле относятся элементы первого множества, ко второму — подмножества (одно подмножество — одна вершина) . Вершины первой и второй долей соединяются ребром, если множество вершины второй доли содержит элемент вершины первого множества. Требуется удалить как можно больше вершин из второй доли с инцидентными ей ребрами, но чтобы каждой вершине первой доли осталось хотя бы одно инцидентное ребро.
Пусть, например, исходное множество содержит 12 элементов <1,2. 12>, а система подмножеств следующая: <2, 3>, <4, 8, 10>, <1, 6>, <6, 9>, <2, 11>, <5, 7>, <4, 5, 12>, <8, 11>, <3, 9>, <11>. Тогда в алгебраической форме (на NP-языке) эта задача выглядит следующим образом
Project Cover2
Module Main2
Var x1 As Boolean
Var x2 As Boolean
Var x3 As Boolean
Var x4 As Boolean
Var x5 As Boolean
Var x6 As Boolean
Var x7 As Boolean
Var x8 As Boolean
Var x9 As Boolean
Var x10 As Boolean
Var x11 As Boolean
Var x12 As Boolean
Con c1 As x2+x3>=1
Con c2 As x4+x8+x10>=1
Con c3 As x1+x6>=1
Con c4 As x6+x9>=1
Con c5 As x2+x11>=1
Con c6 As x5+x7>=1
Con c7 As x4+x5+x12>=1
Con c8 As x8+x11>=1
Con c9 As x3+x9>=1
Con c10 As x11>=1
Con e1 As
Minimize(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12)
Источник
сколькими способами можно распределить 12 комнат под 12 учебных кабинетов
Ответы
Пусть имеем некоторое множество и систему его подмножеств. Требуется найти минимальное количество подмножеств, покрывающих исходное множество. Задачу можно представить с помощью двудольного графа: к первой доле относятся элементы первого множества, ко второму — подмножества (одно подмножество — одна вершина). Вершины первой и второй долей соединяются ребром, если множество вершины второй доли содержит элемент вершины первого множества. Требуется удалить как можно больше вершин из второй доли с инцидентными ей ребрами, но чтобы каждой вершине первой доли осталось хотя бы одно инцидентное ребро.
Пусть, например, исходное множество содержит 12 элементов <1,2. 12>, а система подмножеств следующая: <2, 3>, <4, 8, 10>, <1, 6>, <6, 9>, <2, 11>, <5, 7>, <4, 5, 12>, <8, 11>, <3, 9>, <11>. Тогда в алгебраической форме (на NP-языке) эта задача выглядит следующим образом
Project Cover2
Module Main2
Var x1 As Boolean
Var x2 As Boolean
Var x3 As Boolean
Var x4 As Boolean
Var x5 As Boolean
Var x6 As Boolean
Var x7 As Boolean
Var x8 As Boolean
Var x9 As Boolean
Var x10 As Boolean
Var x11 As Boolean
Var x12 As Boolean
Con c1 As x2+x3>=1
Con c2 As x4+x8+x10>=1
Con c3 As x1+x6>=1
Con c4 As x6+x9>=1
Con c5 As x2+x11>=1
Con c6 As x5+x7>=1
Con c7 As x4+x5+x12>=1
Con c8 As x8+x11>=1
Con c9 As x3+x9>=1
Con c10 As x11>=1
Con e1 As
Minimize(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12)
или
12*12= 144 варианта.
Источник
Теорема сложения вероятности
Теорема сложения вероятностей несовместных событий.Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Теорема сложения вероятностей совместных событий.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Для трех совместных событий имеет место формула
Событие, противоположное событию А (т.е. не наступление события А), обозначают 
. Сумма вероятностей двух противоположных событий равна единице:
Вероятность наступления события А, вычисленная в предположении, что событие В уже произошло, называется условной вероятностью события А при условии В и обозначается 
или 
.
Если А и В 
независимые события, то
Событие А,В,С,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением других событий по отдельности или в любой их комбинации.
Теорема умножения вероятностей
Теорема умножения вероятностей независимых событий.Вероятность совместного появления двух независимых событий равна произведению вероятностей
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле
Теорема умножения вероятностей зависимых событий.Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
Формула полной вероятности. Формула Байеса
Пусть событие (гипотезы) 
образуют полную группу событий и при наступлении каждого из них, например 
, событие А может наступить с некоторой условной вероятностью 
Тогда вероятность наступления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
где 
Формула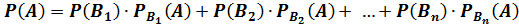 
называется формулой полной вероятности.
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) , которые образуют полную группу событий. Если событие А уже произошло, то вероятность гипотез могут быть переоценены по формуле Байеса(формуле вероятности гипотез):
,
где 
вероятность каждой из гипотез после испытания, в результате которого наступило событие, А; 
условная вероятность события А после наступления события 
а 
находится по формуле полной вероятности
Повторение испытаний. Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимы относительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равна p(где 0 
событие А наступит ровно k раз (безразлично, какой последовательности), находится по формуле Бернулли:
где 
Тема 5.1 Основы теории вероятностей
Исследовательская работа. Решение задач
Упражнения
1.Найдите число размещений: 
2.Вычислите: 
3. 30 учащихся обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?
4.Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
5.Решите уравнения: 
6. Сколькими способами можно составить список из 10 человек?
7.Сколькими способами можно распределить 12 классных комнат под 12 учебных кабинетов?
8. В ящике с деталями оказалось 300 деталей I сорта, 200 деталей II сорта и 50 деталей III сорта. Наудачу вынимают одну из деталей. Чему равна вероятность вынуть деталь I, II или III сорта?
9.В урне находится 20 белых и 15 черных шаров. Наудачу вынимают один шар, который оказался белым, и откладывают его в сторону. После этого берут еще один шар. Найдите вероятность того, что это шар также окажется белым.
10.В ящике в случайном порядке положены 10 деталей, из которых 4 стандартных. Контролер взял наудачу 3 детали. Найдите вероятность того, что хотя бы одна из взятых деталей оказалась стандартной.
11.В урне находится 10 белых, 15 черных, 20 синих и 25 красных шаров. Найдите вероятность того, что вынутый шар окажется: 1) белым; 2) черным или красным.
12.Рабочий обслуживает два автомата, работающих независимо друг от друга. Вероятность того, что в течении часа первый автомат не потребует внимание рабочего, равна 0,8, а для второго автомата эта вероятность равна 0,7. Найдите вероятность того, что в течение часа ни один из автоматов не потребует внимание рабочего.
13.В урне находится 6 шаров, из которых 3 белых. Наудачу вынут один за другим два шара. Вычислите вероятность того, что оба шара окажутся белыми.
14.В урну, содержащую три шара, положили белый шар, после чего из нее наугад вынули один шар. Найдите вероятность того, что извлеченный шар окажется белым, если все возможные предположения о первоначальном составе шаров (по цвету) равновозможные.
15.В ящике сложены детали: 16 деталей с первого участка, 24-со второго и 20-с третьего. Вероятность того, что деталь, изготовленная на втором участке, отличного качества, равна 0,6, а для деталей, изготовленных на первом и третьем участках, вероятности равна 0,8. Найдите вероятность того, что наудачу извлеченная деталь окажется отличного качества.
Источник
Теорема сложения вероятности
Теорема сложения вероятностей несовместных событий.Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Теорема сложения вероятностей совместных событий.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Для трех совместных событий имеет место формула
Событие, противоположное событию А (т.е. не наступление события А), обозначают . Сумма вероятностей двух противоположных событий равна единице:
Вероятность наступления события А, вычисленная в предположении, что событие В уже произошло, называется условной вероятностью события А при условии В и обозначается или .
Если А и В независимые события, то
Событие А,В,С,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением других событий по отдельности или в любой их комбинации.
Теорема умножения вероятностей
Теорема умножения вероятностей независимых событий.Вероятность совместного появления двух независимых событий равна произведению вероятностей
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле
Теорема умножения вероятностей зависимых событий.Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
Формула полной вероятности. Формула Байеса
Пусть событие (гипотезы) образуют полную группу событий и при наступлении каждого из них, например , событие А может наступить с некоторой условной вероятностью Тогда вероятность наступления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
где
Формула 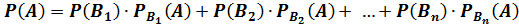называется формулой полной вероятности.
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) , которые образуют полную группу событий. Если событие А уже произошло, то вероятность гипотез могут быть переоценены по формуле Байеса(формуле вероятности гипотез):
,
где вероятность каждой из гипотез после испытания, в результате которого наступило событие, А; условная вероятность события А после наступления события а находится по формуле полной вероятности
Повторение испытаний. Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимы относительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равна p(где 0 событие А наступит ровно k раз (безразлично, какой последовательности), находится по формуле Бернулли:
где
Тема 5.1 Основы теории вероятностей
Исследовательская работа. Решение задач
Упражнения
1.Найдите число размещений:
2.Вычислите:
3. 30 учащихся обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?
4.Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
5.Решите уравнения:
6. Сколькими способами можно составить список из 10 человек?
7.Сколькими способами можно распределить 12 классных комнат под 12 учебных кабинетов?
8. В ящике с деталями оказалось 300 деталей I сорта, 200 деталей II сорта и 50 деталей III сорта. Наудачу вынимают одну из деталей. Чему равна вероятность вынуть деталь I, II или III сорта?
9.В урне находится 20 белых и 15 черных шаров. Наудачу вынимают один шар, который оказался белым, и откладывают его в сторону. После этого берут еще один шар. Найдите вероятность того, что это шар также окажется белым.
10.В ящике в случайном порядке положены 10 деталей, из которых 4 стандартных. Контролер взял наудачу 3 детали. Найдите вероятность того, что хотя бы одна из взятых деталей оказалась стандартной.
11.В урне находится 10 белых, 15 черных, 20 синих и 25 красных шаров. Найдите вероятность того, что вынутый шар окажется: 1) белым; 2) черным или красным.
12.Рабочий обслуживает два автомата, работающих независимо друг от друга. Вероятность того, что в течении часа первый автомат не потребует внимание рабочего, равна 0,8, а для второго автомата эта вероятность равна 0,7. Найдите вероятность того, что в течение часа ни один из автоматов не потребует внимание рабочего.
13.В урне находится 6 шаров, из которых 3 белых. Наудачу вынут один за другим два шара. Вычислите вероятность того, что оба шара окажутся белыми.
14.В урну, содержащую три шара, положили белый шар, после чего из нее наугад вынули один шар. Найдите вероятность того, что извлеченный шар окажется белым, если все возможные предположения о первоначальном составе шаров (по цвету) равновозможные.
15.В ящике сложены детали: 16 деталей с первого участка, 24-со второго и 20-с третьего. Вероятность того, что деталь, изготовленная на втором участке, отличного качества, равна 0,6, а для деталей, изготовленных на первом и третьем участках, вероятности равна 0,8. Найдите вероятность того, что наудачу извлеченная деталь окажется отличного качества.
Источник
