Число написать разными способами

Содержание

Способы записи чисел
Сумма разрядных слагаемых
Сумма разрядных слагаемых
Разряды и классы чисел
Примеры
Развитие речи на уроках математики
Скачать:
Предварительный просмотр:

Способы записи чисел

Человеку необходимо уметь правильно называть и записывать числа, уметь правильно выполнять действия над ними. Для решения этой проблемы люди разных стран изобретали различные системы счисления.

Система счисления – язык для наименования, записи чисел и выполнения действий над ними.

Самой старой системой счисления считается двоичная. Человек вел счет не при помощи пальцев, а при помощи рук. Следы этой системы сохранились и сегодня в стремлении считать парами. В компьютерной технике также используется двоичная система счисления.

Переход к пальцевому счету привел к созданию пятеричной системы, десятеричной и др.

В Древнем Вавилоне считали группам и по 60, система счисления была шестидесятеричная.

Сейчас наиболее широкое применение получила десятичная система счисления, хотя используются и другие:

шестидесятеричная – при измерении времени,

двенадцатеричная – при счете дюжинами,

двоичная – при счете парами и др.

Различают позиционные и непозиционные системы счисления.

Примером непозиционной системы может быть римская нумерация. В ней 7 знаков:

I – один, V – пять, X – десять, L – пятьдесят, С – сто, D – пятьсот, М – тысяча.

Все другие числа получаются из этих семи при помощи двух арифметических действий: сложения и вычитания. Например, IV – четыре

(5 – 1 = 4), VI – шесть (5 + 1 = 6). Записи IV и VI показывают, что римская система счисления непозиционная – где бы не стоял знак V или I – он всегда имеет одно и то же значение.

Примером позиционной системы счисления является используемая повсеместно десятичная система. В ней для записи чисел используется 10 цифр, и значение каждой цифры зависит от места (позиции), которое она занимает в записи числа. Например, в записи 253 цифра 2 обозначает сотни, в записи 325 – цифра 2 обозначает десятки, а в записи 532 – цифра 2 обозначает единицы.

Примечание: Заслушиваются сообщения студентов, предварительно подготовленные на темы:

1) Возникновение и развитие способов записи чисел.

2) Системы счисления разных народов.

Источник

Сумма разрядных слагаемых

О чем эта статья:

Сумма разрядных слагаемых

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:

Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.

30 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.

300, 50, 6 — разрядные слагаемые.

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

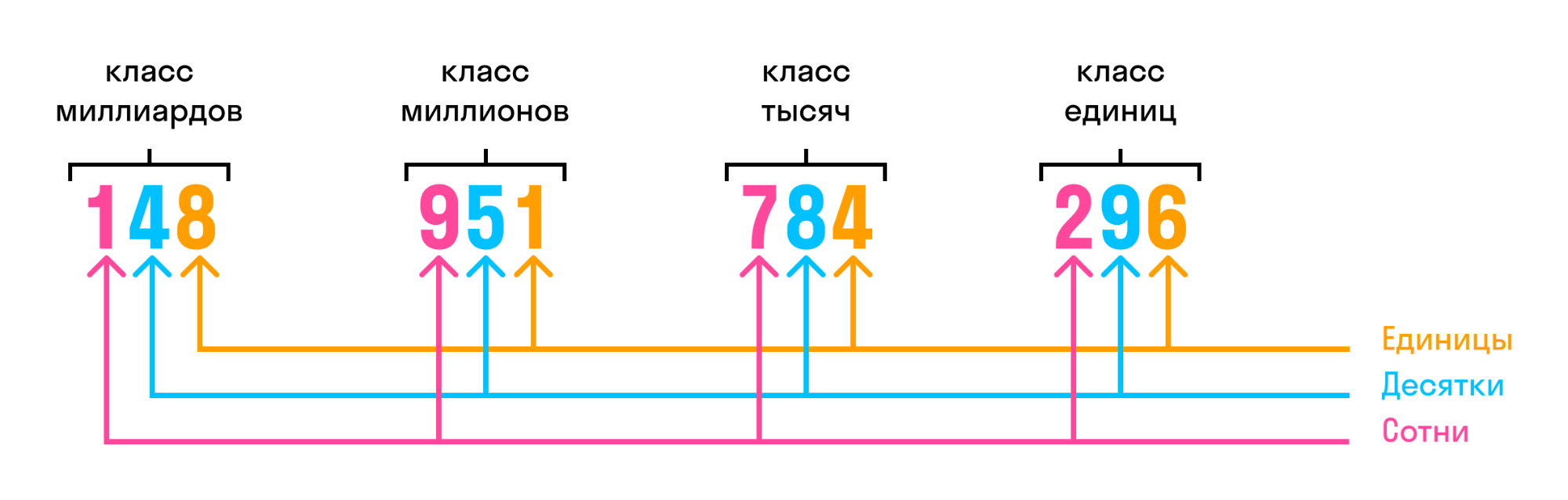
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

Названия классов многозначных чисел:

первый — класс единиц,
второй — класс тысяч,
третий — класс миллионов,
четвёртый — класс миллиардов,
пятый — класс триллионов,
шестой — класс квадриллионов,
седьмой — класс квинтиллионов,
восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

10 единиц = 1 десяток;
10 десятков = 1 сотня;
10 сотен = 1 тысяча;
10 тысяч = 1 десяток тысяч;
10 десятков тысяч = 1 сотня тысяч;
10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.

Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

шести единиц миллионов (6 * 1 000 000);
пяти десятков тысяч (5 * 10 000);
семи единиц тысяч (7 * 1000);
трех сотен (3 * 100);
восьми десятков (8 * 10);
шести единиц (6).

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.

7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

84 610
84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
84 610 = 80 000 + 4 000 + 600 + 10.
45 317
45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
45 317 = 40 000 + 5 000 + 300 + 17.
56 789
56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
56 789 = 50 000 + 6 000 + 700 + 80 + 9.
345 677
345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
687 543
687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
877 589
877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.

4 895 634
4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
8 675 349
8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
77 897 125
77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
656 734 212
656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.

Источник

Развитие речи на уроках математики

Развитие речи на уроках математики

учитель высшей категории, ГБОУ СОШ №390 Санкт-Петербурга

Развитие речи для учащихся начальной школы, а особенно для детей речевых классов, является решающим фактором успешного усвоения программного материала по всем предметам, так как наряду с развитием речи развиваются образное и логическое мышление, память, внимание.

Хочу поделиться опытом работы по развитию речи детей на уроках математики. Наиболее значимая и трудоемкая работа в этом направлении проводится при чтении примеров разными способами, объяснении решения задач и уравнений, разборе многозначных чисел. Для этого учащиеся должны знать наизусть все правила, которые напечатаны в учебнике, названия и обозначения арифметических действий, названия компонентов и результата каждого действия, связь между компонентами и результатом каждого действия; названия и последовательность чисел в натуральном ряду (с какого числа начинается этот ряд и как образуется каждое следующее число в этом ряду); как образуется каждая следующая счетная единица (сколько единиц в одном десятке, сколько десятков в одной сотне и т. д., сколько разрядов содержится в каждом классе), названия и последовательность классов.

Приведу примеры такого вида работ.

Составление рассказа про число по плану (например, число 748):

Прочитай число (семьсот сорок восемь).
Какое оно по количеству знаков, по четности (это трехзначное число, четное).
Какое место занимает в числовом ряду (в числовом ряду стоит после числа 746 и перед числом 749).
Сколько единиц каждого разряда в нем содержится (в этом числе 8 единиц I разряда, 4 единицы II разряда и 7 единиц III разряда).
Сколько в нем содержится отдельных единиц, десятков, сотен и т. д. (в нем содержится отдельных 8 единиц, 4 десятка, 7 сотен).
Сколько в нем содержится всего единиц, десятков, сотен и т. д. (в нем содержится всего 748 единиц, 74 десятка, 7 сотен).
Представить число в виде суммы разрядных слагаемых (число можно представить в виде суммы разрядных слагаемых 700+40+8).

Таким образом, зная план, дети составляют рассказ о любом числе.

Решение уравнений с объяснением.

Вспомнить название чисел при сложении. Прочитать уравнение (первое слагаемое неизвестно, второе слагаемое 23, сумма равна 70).
Рассказать правило нахождения неизвестного числа (чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое или, чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое).
Решаем уравнение

Х-15=30 (уменьшаемое неизвестно, вычитаемое 15, разность равна 30; чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое, решаем уравнение).

50-Х=12 (уменьшаемое 50, вычитаемое неизвестно, разность равна 12; чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность, решаем уравнение).

Х·4=60 (первый множитель неизвестен, второй множитель 4, произведение равно 60; чтобы найти первый множитель, надо произведение разделить на второй множитель или, чтобы найти неизвестный множитель, надо произведение разделить на известный множитель, решаем уравнение).

Х:10=8 (делимое неизвестно, делитель 10, частное равно 8; чтобы найти делимое, надо частное умножить на делитель, решаем уравнение).

72:Х=6 (делимое 72, делитель неизвестен, частное равно 6; чтобы найти делитель, надо делимое разделить на частное, решаем уравнение).

Решение задач с объяснением.

При решении задач используются методы синтеза (разбор задачи от условия к главному вопросу) и анализа (разбор задачи от главного вопроса к условию). Наиболее эффективно идет работа над разбором задачи, когда применяются оба метода.

На школьной фотовыставке было представлено 35 цветных фотографий, а черно-белых на 25 фотографий больше. Сколько всего фотографий было на выставке?

Чтобы узнать, сколько всего фотографий было на выставке, мы должны знать, сколько было цветных фотографий и черно-белых. Сколько было цветных, мы знаем, а сколько черно-белых нет, но можем узнать. Зная, что цветных фотографий было 35, а черно-белых на 25 фотографий больше, мы можем узнать, сколько черно-белых фотографий было на выставке действием сложения (записываем 1.) 35+25=60(ф.)-черно-белых). Зная, что цветных фотографий было 35, а черно-белых 60, мы можем узнать, сколько всего фотографий было на выставке действием сложения (записываем

2.) 60+35=95(ф.). Мы ответили на главный вопрос задачи. Ответ: всего 95 фотографий было на выставке.

Чтение примеров разными способами.

20+6

— к 20 прибавить 6;

— 20 увеличить на 6;

— найти сумму чисел 20 и 6 (если не говорить слово чисел, то числительные склоняются – найти сумму двадцати и шести);

— первое слагаемое 20, второе слагаемое 6, найти сумму.

20-6

— из 20 вычесть 6;

— 20 уменьшить на 6;

— найти разность чисел 20 и 6 (если не говорить слово чисел, то числительные склоняются – найти разность двадцати и шести);

— уменьшаемое 20, вычитаемое 6, найти разность;

— на сколько 20 больше 6 или на сколько 6 меньше 20.

Подобным образом читаются примеры на умножение и деление.

70-30·5

— из числа 70 (из семидесяти) вычесть произведение чисел 30 и 5 (тридцати и пяти);

— уменьшаемое 70, вычитаемое выражено произведением чисел 30 и 5 (тридцати и пяти);

(50+30):5

— сумму чисел 50 и 30 (пятидесяти и тридцати) разделить на 5;

— сумму чисел 50 и 30 (пятидесяти и тридцати) уменьшить в 5 раз;

— делимое выражено суммой чисел 50 и 30, делитель 5.

52:3+45·2

— к частному чисел 52 и 3(пятидесяти двух и трех) прибавить произведение чисел 45 и 2 (сорока пяти и двух);

— первое слагаемое выражено частным чисел 52 и 3, второе слагаемое выражено произведением чисел 45 и 2.

Скачать:

Вложение	Размер
razvitie_rechi_na_urokakh_matematiki.docx	23.38 КБ

Предварительный просмотр:

Развитие речи на уроках математики

учитель высшей категории, ГБОУ СОШ №390 Санкт-Петербурга

Приведу примеры такого вида работ.

Составление рассказа про число по плану (например, число 748):

Прочитай число ( семьсот сорок восемь ).
Какое оно по количеству знаков, по четности ( это трехзначное число, четное ).
Какое место занимает в числовом ряду ( в числовом ряду стоит после числа 746 и перед числом 749).
Сколько единиц каждого разряда в нем содержится ( в этом числе 8 единиц I разряда, 4 единицы II разряда и 7 единиц III разряда ).
Сколько в нем содержится отдельных единиц, десятков, сотен и т. д. ( в нем содержится отдельных 8 единиц, 4 десятка, 7 сотен ).
Сколько в нем содержится всего единиц, десятков, сотен и т. д. ( в нем содержится всего 748 единиц, 74 десятка, 7 сотен ).
Представить число в виде суммы разрядных слагаемых ( число можно представить в виде суммы разрядных слагаемых 700+40+8 ).

Таким образом, зная план, дети составляют рассказ о любом числе.

Решение уравнений с объяснением.

Вспомнить название чисел при сложении. Прочитать уравнение ( первое слагаемое неизвестно, второе слагаемое 23, сумма равна 70 ).
Рассказать правило нахождения неизвестного числа ( чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое или, чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое ).
Решаем уравнение

Х-15=30 ( уменьшаемое неизвестно, вычитаемое 15, разность равна 30; чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое, решаем уравнение ).

50-Х=12 ( уменьшаемое 50, вычитаемое неизвестно, разность равна 12; чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность, решаем уравнение ).

Х·4=60 ( первый множитель неизвестен, второй множитель 4, произведение равно 60; чтобы найти первый множитель, надо произведение разделить на второй множитель или, чтобы найти неизвестный множитель, надо произведение разделить на известный множитель, решаем уравнение ).

Х:10=8 ( делимое неизвестно, делитель 10, частное равно 8; чтобы найти делимое, надо частное умножить на делитель, решаем уравнение ).

72:Х=6 ( делимое 72, делитель неизвестен, частное равно 6; чтобы найти делитель, надо делимое разделить на частное, решаем уравнение).

Решение задач с объяснением.

Чтобы узнать, сколько всего фотографий было на выставке, мы должны знать, сколько было цветных фотографий и черно-белых. Сколько было цветных, мы знаем, а сколько черно-белых нет, но можем узнать. Зная, что цветных фотографий было 35, а черно-белых на 25 фотографий больше, мы можем узнать, сколько черно-белых фотографий было на выставке действием сложения (записываем 1.) 35+25=60(ф.)-черно-белых). Зная, что цветных фотографий было 35, а черно-белых 60, мы можем узнать, сколько всего фотографий было на выставке действием сложения (записываем

2.) 60+35=95(ф.). Мы ответили на главный вопрос задачи. Ответ: всего 95 фотографий было на выставке.

Чтение примеров разными способами.

— к 20 прибавить 6;

— 20 увеличить на 6;

— найти сумму чисел 20 и 6 (если не говорить слово чисел , то числительные склоняются – найти сумму двадцати и шести );

— первое слагаемое 20, второе слагаемое 6, найти сумму.

— из 20 вычесть 6;

— 20 уменьшить на 6;

— найти разность чисел 20 и 6 ( если не говорить слово чисел , то числительные склоняются – найти разность двадцати и шести );

— уменьшаемое 20, вычитаемое 6, найти разность;

— на сколько 20 больше 6 или на сколько 6 меньше 20.

Подобным образом читаются примеры на умножение и деление.

— из числа 70 (из семидесяти) вычесть произведение чисел 30 и 5 (тридцати и пяти);

— уменьшаемое 70, вычитаемое выражено произведением чисел 30 и 5 (тридцати и пяти);

— сумму чисел 50 и 30 (пятидесяти и тридцати) разделить на 5;

— сумму чисел 50 и 30 (пятидесяти и тридцати) уменьшить в 5 раз;

— делимое выражено суммой чисел 50 и 30, делитель 5.

— к частному чисел 52 и 3(пятидесяти двух и трех) прибавить произведение чисел 45 и 2 (сорока пяти и двух);

— первое слагаемое выражено частным чисел 52 и 3, второе слагаемое выражено произведением чисел 45 и 2.

Источник