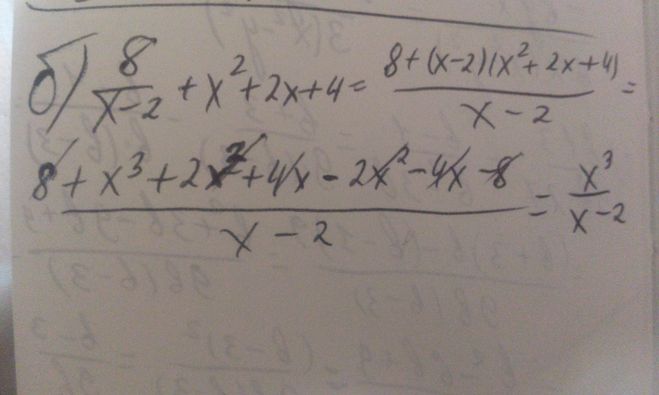Чем отличается арифметический способ от алгебраического

В чем отличие арифметического от алгебраического способа решения задач?

Арифметический — это по сути способ рассуждений. А алгебраический — это составление уравнений.

Вот возьмем для примера знаменитую задачу из рассказа Чехова «Репетитор».

Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?

Алгебраический способ такой:

Пусть купец купил x аршин синего и y аршин черного сукна.

Решаем систему и получаем

А арифметический способ такой. Представим себе, что он купил только черное сукно, все 138 аршин по 3 руб.

Тогда он заплатил бы 138*3 = 414 руб. А он заплатил 540 руб. Значит, остальные 540-414=126 руб. он заплатил за синее сукно.

Синее стоит дороже на 2 руб за каждый аршин. А он заплатил лишних 126 руб.

Значит, он купил 126/2 = 63 аршина синего сукна. Тогда черного он купил 138 — 63 = 75 аршин.

И очень жаль, что в школе постепенно отказываются от арифметического способа и всё решают уравнениями.

Кстати, в рассказе репетитор — сам ученик 7 класса — как раз не знал арифметического способа и не смог решить эту задачу, хотя она для 3 класса. А иксов ученик в 3 классе еще не проходил.

В арифметике с применением конкретных чисел записанных только цыфрами. А в алгебре вы решаете задачи с неизвестными числами, обобщённые значения которых выражены символами в виде латинских букв.

Затем уже в решение из символов (букв) вы можете подставить конкретные числа выраженные цыфрами и решить уже ставшую конкретной арифметическую задачу.

Проще сказать отличие в следующем:

В арифметической задаче вы ищите конкретный числовой ответ, а в алгебраической задаче вы ищите обобщённый ответ для всех возможных числовых значений выраженный в алгебраических символах.

Часто родители,а иногда и ученики,задают «хитрые» задачки для 2-3 класса,все начинают помогать через х и у ,а родители говорят:»ну как ребёнку объяснить эти иксы.А задача решается просто арифметическим способом.Простой пример:На почте приняли 7 больших посылок, каждая массой 9 кг, и 5 маленьких. Какова масса маленькой посылки, если масса всех посылок получилась 78 кг?Арифметический способ:7*9=63кг,2)78-63=15 кг 3)15\5=3(кг)-масса маленькой посылки.Алгебраический способ:х-вес маленькой посылки.уравнение:5х+7*9=78,х=3,но чаще бывают более сложные задачи,эта наипростейшая.Но смысл тот же.

Это уравнение является линейным, поэтому для его решения необходимо:

1) Раскрыть скобки в левой и в правой части.

2) Привести подобные слагаемые.

3) Слагаемые с x перенести в левую часть, числовые слагаемые перенести в правую часть.

Итак, решим уравнение 0,4 (3x — 0,5) = 1,5x + 0,2 (x + 1).

0,4 * 3x — 0,4 * 0,5 = 1,5x + 0,2x + 0,2.

1,2x — 0,2 = 1,7x + 0,2.

Значит, корень уравнения x = -0,8.

0,4 * (3 * (-0,8) — 0,5) = 1,5 * (-0,8) + 0,2 (-0,8 + 1).

0,4 * (-2,9) = -1,2 + 0,04.

Верно. Значит, корень данного уравнения был найден правильно.

Вас нужно лишь применить правила приведения дробей, раскрытие скобок и сумма квадратов.

1) Умножаем правую часть, чтобы получить дробь. Раскрываем скобки и приводим подоные члены.

2) Действуем аналогично, обращая внимания на знаки. Заметим, что (x-y)*(x+y)=x^2-y^2

3) Можем вынести 9 за скобки, а во второй дроби b. Тогда будет легче привести к общему знаменателю.

Пусть V — скорость автобуса, t — время в часах, за который автобус догнал первого велосипедиста.

Автобус проехал за t часов столько же, сколько велосипедист за t+1 час, расстояние равно скорость умножить на время, считаем и приравниваем расстояния, которые проехали автобус и первый велосипедист, получаем

Второго велосипедиста автобус догнал через 10 минут = 1/6 часа после того, как первого, то есть через t+1/6 часов после начала своего движения, второй велосипедист к тому времени ехал 1+t+1/6 часов, делаем то же самое, что для первого велосипедиста, получаем

Итак, у нас есть система из двух уравнений с двумя неизвестными

Вычтем из второго первое, получим

1/6V=5(1+t)+20/6, домножим обе части на 6, получим V=30(1+t)+20, упростим, получим V=30t+50, подставим в первое уравнение:

30t^2+50t=15+15t, где t^2 — это t в квадрате. Перенесём всё в одну часть и сократим на 5, получим

Это квадратное уравнение имеет два корня, положительный и отрицательный, время отрицательным быть не может, значит, нужно найти положительный корень.

По формуле это t=(корень<7*7+3*4*6>-7)/(2*6)=(11-7)/12=1/3

Подставим значение t в полученное ранее V=30t+50, получим V=10+50=60, то есть скорость автобуса — 60 км/ч.

Для решения этого уравнения достаточно 204 умножить на 59.

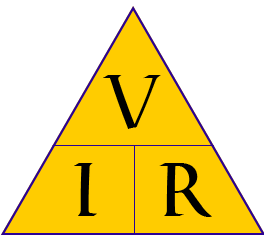
Вообще, любой подобное уравнение решается достаточно просто, методом треугольника: представьте себе в виде треугольника три цифры: одна цифра в верхнем углу треугольника и две цифры расположены по нижним углам. В верхнем углу — результат произведения умножаемого и множителя, расположенных в двух нижних углах. Закрыв рукой неизвестное — у нас на картинке сразу появится необходимое действие, для нахождения неизвестного.

На картинке отображен треугольник в виде закона Ома.

Чтобы найти V нам необходимо перемножить I и R. Чтобы найти R нам необходимо разделить V на I.

Общий ход графического решения задач. Сначала, при необходимости, как в обычных алгебраических уравнениях, можете переносить любые члены из левой части в правую или наоборот, не забыв при этом поменять знак, добиваясь, чтобы в каждой части уравнения были удобные для Вас выражения. Затем пишете функции у(л)=(левая часть уравнения) и у(п)=(правая часть уравнения). Строите графики функций у(л) и у(п). Абсциссы точек пересечения графиков (если таковые есть), дают Вам решения Вашего уравнения.

В Ваших уравнениях левая и правая части уравнений приведены к оптимальному виду.

Значит, для решения уравнения (2) Вам нужно построить графики функций y=√(x) и у=2, для решения уравнения (4) — графики функций y=√(x) и у=-х.

Берете отдельный листок в клетку. Чертите на ней оси координат с пересечением осей в центре листочка. Как можно аккуратнее и точнее чертите на нем параболу y=X^2, и обязательно прочерчиваете ось Y. Аккуратно наклеиваете листочек на картон или тонкий пластик. Аккуратно ножницами вырезаете эту параболу. Теперь у вас готов шаблон для построения графиков любых парабол.

Построение графика функции y=√(x). На странице тетради в клетку чертите оси координат. Берете изготовленный шаблон, и накладываете его горизонтально на страницу так, чтобы начала координат шаблона и в тетради совпали, о ось Y шаблона совпала с осью Х в тетради. Обводите карандашом верхнюю половину шаблона. На листочке получится половинка параболы, расположенная горизонтально. Это и есть график функции y=√(x).

Решение задачи (2). Через точку (0,5) проводите прямую, параллельную оси Х. Точка пересечения этой прямой с параболой (25,5) даст решение примера. Х=25.

Решение задачи (4). Через центр координат проводите диагональ второй и четвертой четвертей. Это будет график функции y=-x. У этой прямой и параболы имеется только одна общая точка (0;0), т.е. начало координат. Значит решением является х=0,

Источник

Решение задач алгебраическим и арифметическим способом

Описание презентации по отдельным слайдам:

Описание слайда:

Урок математики в 4 классе
«Решение задач алгебраическим и арифметическим способом»
Учитель начальных классов МОУ СОШ №5 г.о. Кохма Ивановской обл.
Щапова Наталия Станиславовна

Описание слайда:

«Всякая хорошо решённая задача доставляет умственное наслаждение».
Г.Гессе

Описание слайда:

Вперёд! В «Мир математических задач».

Описание слайда:

Описание слайда:

На палубе сидят Иванов, Петров, Марков и Карпов. Их имена: Андрей, Сергей, Тимофей и Алексей. Известно:
а) что Иванов не Алексей и не Андрей;
б) Сергей сидит между Марковым и Тимофеем;
в) Карпов не Сергей и не Алексей;
г) Петров сидит между Карповым и Андреем.
Как зовут Иванова, Петрова, Маркова и Карпова?

Описание слайда:

Иванов Сергей
Петров Алексей
Марков Андрей
Карпов Тимофей

Описание слайда:

Корабельный кок принял на борт 7 больших коробок, каждая массой 9 кг, и 5 маленьких. Какова масса маленькой коробки, если масса всех коробок составила 78 кг?
(х × 5) (кг)
(9 × 7) (кг)
(х × 5 + 9 × 7) (кг)

Описание слайда:

На путешествие в шторм уходит времени в 3 раза больше, чем в хорошую погоду. Сколько времени займет наше путешествие в хорошую и штормовую погоду, если разница во времени составляет 12 часов?
12 ч.

Описание слайда:

Описание слайда:

Масса двух рыб составляла 11 кг. Найдите массу каждой рыбы, если одна из них легче другой на 3 кг.

Описание слайда:

На борт корабля было поднято две бочки с пресной водой одинаковой емкости. Когда из первой было израсходовано 28 л, а из второй – 45 л, то в ней осталось вдвое меньше воды, чем в первой. Сколько было взято воды на борт корабля?

Описание слайда:

Какие способы решения задач мы повторили?
Арифметический и алгебраический способы решения задач.
Объясните, в чем отличие арифметического способа решения задач от алгебраического?
Решая задачу алгебраическим способом, обозначают неизвестную величину буквой, составляют уравнение по условию задачи и решают его. Когда задача решается арифметическим способом, уравнение не составляют.
Арифметический способ мы фактически применяли один – способ уравнивания. Подумайте, почему он получил такое название?
Способ уравнивания заключается в том, что первым шагом во всех случаях было уравнивание двух величин. Это хорошо видно, если представить условие задачи в виде схемы.

Описание слайда:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Охрана труда

• Сейчас обучается 95 человек из 44 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 334 человека из 66 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 171 человек из 47 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Международная дистанционная олимпиада Осень 2021

Похожие материалы

Палитра

Знакомство. Введение знака «Поднятая рука»

Слова с сочетаниями ЖИ-ШИ

Картины Ивана Ивановича Шишкина 1832-1898

Речевые таблицы

Спорт

Немного об этикете

Решение уравнений

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5311227 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В проекте КоАП отказались от штрафов для школ

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

ЕСПЧ запретил учителям оскорблять учеников

Время чтения: 3 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник