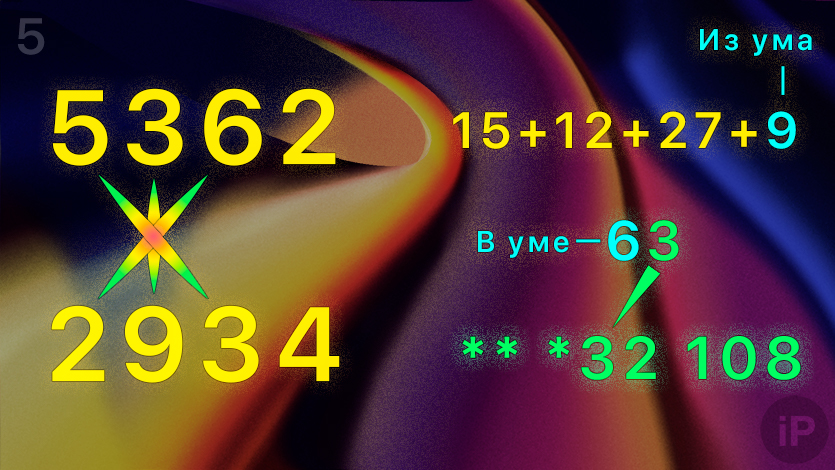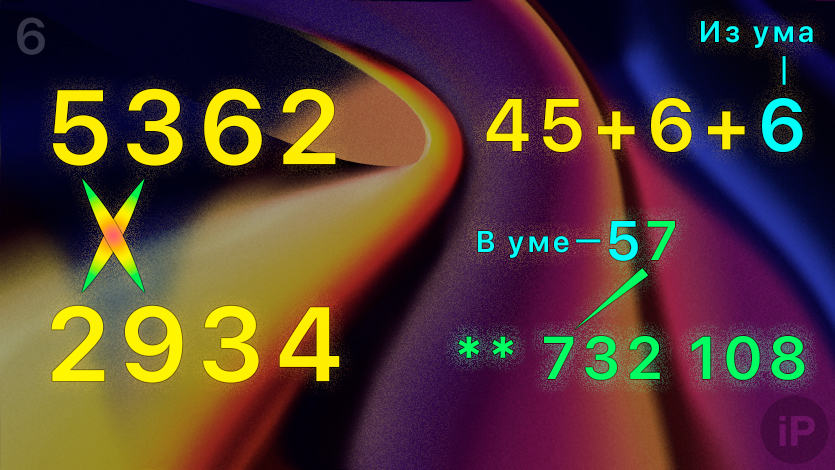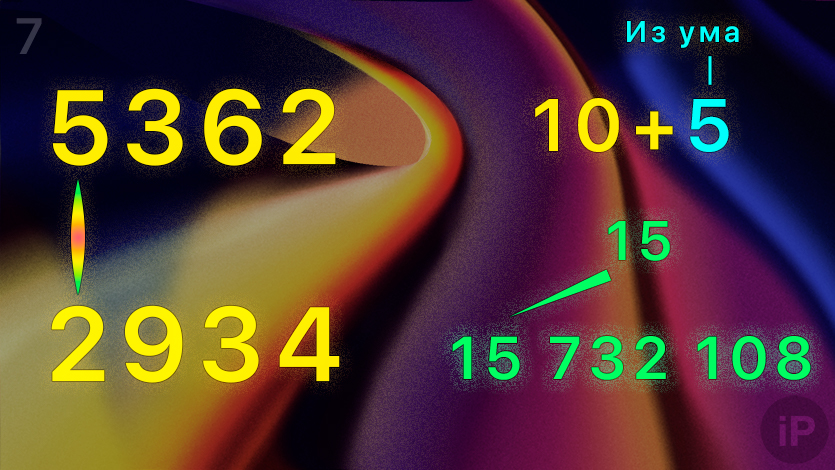Быстрые способы перемножения чисел

Математики обнаружили идеальный способ перемножения чисел

Разбивая крупные числа на мелкие, исследователи превысили фундаментальное математическое ограничение скорости

Четыре тысячи лет назад жители Вавилонии изобрели умножение. А в марте этого года математики усовершенствовали его.

18 марта 2019 два исследователя описали самый быстрый из известных методов перемножения двух очень больших чисел. Работа отмечает кульминацию давнишнего поиска наиболее эффективной процедуры выполнения одной из базовых операций математики.

«Все думают, что метод умножения, который они учили в школе, наилучший, но на самом деле в этой области идут активные исследования», — говорит Йорис ван дер Хувен, математик из Французского национального центра научных исследований, один из соавторов работы.

Сложность множества вычислительных задач, от подсчёта новых цифр числа π до обнаружения крупных простых чисел сводится к скорости перемножения. Ван дер Хувен описывает их результат как назначение своего рода математического ограничения скорости решения множества других задач.

«В физике есть важные константы типа скорости света, позволяющие вам описывать всякие явления, — сказал ван дер Хувен. – Если вы хотите знать, насколько быстро компьютеры могут решать определённые математические задачи, тогда перемножение целых чисел возникает в виде некоего базового строительного блока, по отношению к которому можно выразить такую скорость».

Почти все учатся перемножать числа одинаково. Записываем числа в столбик, перемножаем верхнее число на каждую цифру нижнего (с учётом разрядов) и складываем результат. При перемножении двух двузначных чисел приходится проделать четыре более мелких перемножения для получения итогового результата.

Школьный метод «переноса» требует выполнения n 2 шагов, где n – количество цифр в каждом из перемножаемых чисел. Вычисления с трёхзначными числами требуют девяти перемножений, а со стозначными – 10 000.

Метод переноса нормально работает с числами, состоящими из нескольких цифр, однако начинает буксовать при перемножении чисел, состоящих из миллионов или миллиардов цифр (чем и занимаются компьютеры при точном подсчёте π или при всемирном поиске больших простых чисел). Чтобы перемножить два числа с миллиардом цифр, нужно будет произвести миллиард в квадрате, или 10 18 , умножений, – на это у современного компьютера уйдёт порядка 30 лет.

Несколько тысячелетий считалось, что быстрее перемножать числа нельзя. Затем в 1960 году 23-летний советский и российский математик Анатолий Алексеевич Карацуба посетил семинар, который вёл Андрей Николаевич Колмогоров, советский математик, один из крупнейших математиков XX века. Колмогоров заявил, что не существует обобщённого способа умножения, требующего меньше, чем n 2 операций. Карацуба решил, что такой способ есть – и после недели поисков он его обнаружил.

Анатолий Алексеевич Карацуба

Умножение Карацубы заключается в разбиении цифр числа и повторной их комбинации новым способом, который позволяет вместо большого количества умножений провести меньшее количество сложений и вычитаний. Метод экономит время, поскольку на сложения уходит всего 2n шагов вместо n 2 .

Традиционный метод умножения 25х63 требует четыре умножения на однозначное число и несколько сложений

Умножение Карацубы 25х63 требует трёх умножений на однозначное число и несколько сложений и вычитаний.
a) разбиваем числа
b) перемножаем десятки
c) перемножаем единицы
d) складываем цифры
e) перемножаем эти суммы
f) считаем e – b – c
g) собираем итоговую сумму из b, c и f

При росте количества знаков в числах метод Карацубы можно использовать рекурсивно.

Традиционный метод умножения 2531х1467 требует 16 умножений на однозначное число.

Умножение Карацубы 2531х1467 требует 9 умножений.

«Сложение в школе проходят на год раньше, потому что это гораздо проще, оно выполняется за линейное время, со скоростью чтения цифр слева направо», — сказал Мартин Фюрер, математик из Пенсильванского государственного университета, создавший в 2007 быстрейший на то время алгоритм умножения.

Имея дело с крупными числами, умножение Карацубы можно повторять рекурсивно, разбивая изначальные числа почти на столько частей, сколько в них знаков. И с каждым разбиением вы меняете умножение, требующее выполнения многих шагов, на сложение и вычитание, требующие куда как меньше шагов.

«Несколько умножений можно превратить в сложения, учитывая, что с этим компьютеры будут справляться быстрее», — сказал Дэвид Харви, математик из Университета Нового Южного Уэльса и соавтор новой работы.

Метод Карацубы сделал возможным умножать числа с использованием лишь n 1,58 умножений на однозначное число. Затем в 1971 году Арнольд Шёнхаге и Фолькер Штрассен опубликовали метод, позволяющий умножать большие числа за n × log n × log(log n) небольших умножений. Для умножения двух чисел из миллиарда знаков каждое метод Карацубы потребует 165 трлн шагов.

Йорис ван дер Хувен, математик из Французского национального центра научных исследований

Метод Шёнхаге-Штрассена используется компьютерами для умножения больших чисел, и привёл к двум другим важным последствиям. Во-первых, он ввёл в использование технику из области обработки сигналов под названием быстрое преобразование Фурье. С тех пор эта техника была основой всех быстрых алгоритмов умножения.

Во-вторых, в той же работе Шёнхаге и Штрассен предположили возможность существования ещё более быстрого алгоритма – метода, требующего всего n × log n умножений на один знак – и что такой алгоритм будет наибыстрейшим из возможных. Это предположение было основано на ощущении, что у такой фундаментальной операции, как умножение, ограничение операций должно записываться как-то более элегантно, чем n × log n × log(log n).

«Большинство в общем-то сошлось на том, что умножение – это такая важная базовая операция, что с чисто эстетической точки зрения ей требуется красивое ограничение по сложности, — сказал Фюрер. – По опыту мы знаем, что математика базовых вещей в итоге всегда оказывается элегантной».

Нескладное ограничение Шёнхаге и Штрассена, n × log n × log(log n), держалось 36 лет. В 2007 году Фюрер побил этот рекорд, и всё завертелось. За последнее десятилетие математики находили всё более быстрые алгоритмы умножения, каждый из которых постепенно подползал к отметке в n × log n, не совсем достигая её. Затем в марте этого года Харви и ван дер Хувен достигли её.

Их метод является улучшением большой работы, проделанной до них. Он разбивает числа на знаки, использует улучшенную версию быстрого преобразования Фурье и пользуется другими прорывами, сделанными за последние 40 лет. «Мы используем быстрое преобразование Фурье гораздо более грубо, используем его несколько раз, а не один, и заменяем ещё больше умножений сложением и вычитанием», — сказал ван дер Хувен.

Алгоритм Харви и ван дер Хувена доказывает, что умножение можно провести за n × log n шагов. Однако он не доказывает отсутствия более быстрого метода. Гораздо сложнее будет установить, что их подход максимально быстрый. В конце февраля команда специалистов по информатике из Орхусского университета опубликовала работу, где утверждает, что если одна из недоказанных теорем окажется верной, то этот метод и вправду будет скорейшим из способов умножения.

И хотя в теории этот новый алгоритм весьма важен, на практике он мало что поменяет, поскольку лишь немного выигрывает у уже используемых алгоритмов. «Всё, на что мы можем надеяться, это на трёхкратное ускорение, — сказал ван дер Хувен. – Ничего запредельного».

Кроме того, поменялись схемы компьютерного оборудования. Двадцать лет назад компьютеры выполняли сложение гораздо быстрее умножения. Разрыв в скоростях умножения и сложения с тех пор серьёзно уменьшился, в результате чего на некоторых чипах умножение может даже обгонять сложение. Используя определённые виды оборудования, «можно ускорить сложение, заставляя компьютер умножать числа, и это какое-то безумие», — сказал Харви.

Оборудование меняется со временем, но лучшие алгоритмы своего класса вечны. Вне зависимости от того, как компьютеры будут выглядеть в будущем, алгоритм Харви и ван дер Хувена всё ещё будет самым эффективным способом умножать числа.

Источник

Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?

В школе всё время слышал «где мне пригодится эта математика?».

И сам задавался таким вопросом. А сейчас вот не хватает учебника для «раскачки» извилин. Например, было бы заметно удобнее считать утерянные цены на Apple или выравнивать пиксельную сетку для иллюстраций.

Но не всё потеряно. Умножать числа в любом возрасте считают проверенным способом подточить ум и даже улучшить психическое здоровье.

Ниже расскажу, где оно ещё может пригодиться и что за секретный способ умножения прокачает ваше знание цифр до уровня интуиции.

Крупный счёт прокачает решение бытовых вопросов

Как любому компьютеру нужно расширять оперативную память, так и нашему мозгу нужен отсек для быстрых операций.

Тренировки с умножением укрепят краткосрочную память. Вы перестанете забывать, закрыли ли дверь на ключ, сколько яиц лежало в холодильнике перед походом в магазин и о чём вели речь после того, как отвлеклись.

Не говоря о том, что будете мгновенно считать, во сколько обойдётся вон тот сочный кусок мяса на шашлык или заправка автомобиля, чтобы доехать до соседнего города.

Вам нужна только математика начальной школы

Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:

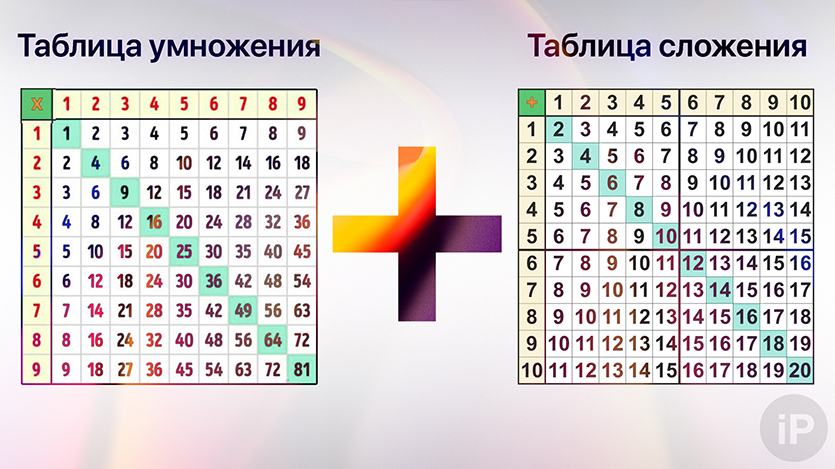
I. Знать таблицу умножения
II. Складывать числа

Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.

Отточить умножение поможет приложение УмноЖатель

Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.

Быстро складывать получится точно таким же постоянным запоминанием.

Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.

На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.

Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:

8+5 = 8+2+3 = 10+3 = 13

В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.

Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.

Операции с умножением тысячей в уме можно разделить на два типа: умножение на однозначные и многозначные числа.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

3864 = 3000 + 800 + 60 + 4

2. Умножаем каждый кусочек на второе число.

3000∙7 = 21000 | 800∙7 = 5600 | 60∙7 = 420 | 4∙7 = 28

3. Разбиваем результаты на простые группы одного размера.

21000 = 20000+1000 | 5600=5000+600 | 420 = 400+20 | 28 = 20+8

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 1000+5000 + 600+400 + 20+20 + 8

20000 + 6000 + 1000 + 40 + 8

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел . Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

0. Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

Источник