Булевы функции

Содержание

1 Понятие булевой функции

В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п. Так или иначе область определения – непрерывное множество. В курсе дискретной математики изучаться должны функции, область определения которых – дискретное множество * . Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов. * Так мы и приходим к понятию булевой функции.

Определение 1 (Булева функция). Булевой функцией от n аргументов называется функция f из n -ой степени множества < 0, 1 >в множество < 0, 1 >.

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству < 0, 1 >. Множество < 0, 1 >мы будем в дальнейшем обозначать через B .

Булеву функцию от n аргументов можно рассматривать как n -местную алгебраическую операцию на множестве B . При этом алгебра W >, где W – множество всевозможных булевых функций, называется алгеброй логики .

Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 n наборов. Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:

x 1	x 2	.	x n- 1	x n	f
0	0	.	0	0	f(0,0. 0,0)
0	0	.	0	1	f(0,0. 0,1)
0	0	.	1	0	f(0,0. 1,0)
0	0	.	1	1	f(0,0. 1,1)
.	.	.	.	.	.
1	1	.	0	0	f(1,1. 0,0)
1	1	.	0	1	f(1,1. 0,1)
1	1	.	1	0	f(1,1. 1,0)
1	1	.	1	1	f(1,1. 1,1)

Раз у нас есть стандартный порядок записывания наборов, то для того, чтобы задать функцию, нам достаточно выписать значения f (0,0. 0,0) , f (0,0. 0,1) , f (0,0. 1,0) , f (0,0. 1,1). f (1,1. 0,0) , f (1,1. 0,1) , f (1,1. 1,0) , f (1,1. 1,1). Этот набор называют вектором значений функции .

Таким образом, различных функций n переменных столько, сколько различных двоичных наборов длины 2 n * . А их 2 в степени 2 n .

Множество B содержит два элемента – их можно рассматривать как булевы функции от нуля (пустого множества) переменных – константу 0 и константу 1 .

Функций от одной переменной четыре: это константа 0, константа 1, тождественная функция , т.е. функция, значение которой совпадает с аргументом и так называемая функция « отрицание ». Отрицание будем обозначать символом ¬ как унарную операцию. Приведём таблицы этих четырёх функций:

x	0	x	¬ x	1
0	0	0	1	1
1	0	1	0	1

Как видим, функции от некоторого числа переменных можно рассматривать как функции от большего числа переменных. При этом значения функции не меняется при изменении этих «добавочных» переменных. Такие переменные называются фиктивными , в отличие от остальных – существенных .

Определение 2 (Фиктивные и существенные переменные). Переменная x i называется фиктивной (несущественной) переменной функции f ( x 1 ,···,x n ), если f ( x 1 ,···,x i- 1 ,0 ,x i+ 1 ,···,x n ) = f ( x 1 ,···,x i- 1 ,1 ,x i+ 1 ,···,x n ) для любых значений x 1 ,···,x i- 1 ,x i+ 1 ,···,x n . Иначе переменная x i называется существенной .

Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций (только те, которые существенно зависят от обеих переменных) мы приводим в следующей таблице:

x 1	x 2	x 1 & x 2	x 1 Ъ x 2	x 1 Й x 2	x 1 Е x 2	x 1 є x 2	x 1 | x 2
0	0	0	0	1	0	1	0
0	1	0	1	1	1	0	1
1	0	0	1	0	1	0	1
1	1	1	1	1	0	1	1

Эти функции записываются как бинарные операции в инфиксной нотации. x 1 & x 2 называется конъюнкцией , x 1 Ъ x 2 – дизъюнкцией , x 1 Й x 2 – импликацией , x 1 є x 2 – эквивалентностью , x 1 Е x 2 – суммой по модулю 2 , x 1 | x 2 – штрихом Шеффера .

Значения 0 и 1 часто интерпретируют как «ложь» и «истину». Тогда понятным становится название функции «отрицание» – она меняет «ложь» на «истину», а «истину» на «ложь». Отрицание читается как «не». Конъюнкция читается обычно как «и» – действительно, конъюнкция равна 1 тогда и только тогда, когда равны 1 и первая и вторая переменная. * Кроме x 1 & x 2 часто используют обозначение x 1 Щ x 2 или x 1 · x 2 или x 1 x 2 или min( x 1 ,x 2 ). Дизъюнкция читается «или» – дизъюнкция равна 1 тогда и только тогда, когда равны 1 первая или вторая переменная. * Импликация выражает факт, что из x 1 следует x 2 . * Импликацию часто также обозначают x 1 ® x 2 .

2 Суперпозиция функций

Определение 3 (Суперпозиция функций). Суперпозицией булевых функций f 0 и f 1 . f n называется функция f ( x 1 . x m ) = f 0 ( g 1 ( x 1 . x m ) . g k ( x 1 . x m )), где каждая из функций g i ( x 1 , . x m ) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f 1 . f n .

Пример 1 (суперпозиция функций).

Функция f ( x,y ) = ¬ ( x & y ) является суперпозицией функций ¬ и &. Функция g ( x,y ) = x Е ( x Ъ y ) является суперпозицией функций Е и Ъ . Функция h ( x,y,z ) = ( x & y ) Е z является суперпозицией функций Е и &. Построим таблицы этих функций.

Суперпозицию ( x & y ) Е ( ¬x Ъ ¬y ) можно прочитать как « x и y плюс не x или не y ».

Следующие соотношения могут быть проверены прямым сравнением значений функций в левой и правой части соотношения на всевозможных наборах аргументов.

1. x & y = y & x
2. x Ъ y = y Ъ x
3. x Е y = y Е x
4. x & ( y & z ) = ( x & y ) & z
5. x Ъ ( y Ъ z ) = ( x Ъ y ) Ъ z
6. x Е ( y Е z ) = ( x Е y ) Е z
7. x Ъ ( y & z ) = ( x Ъ y ) & ( x Ъ z )
8. x & ( y Ъ z ) = ( x & y ) Ъ ( x & z )
9. ¬¬x = x
10. ¬ ( x & y ) = ¬x Ъ ¬y
11. ¬ ( x Ъ y ) = ¬x & ¬y
12. x & x = x
13. x & ¬x = 0
14. x & 0 = 0
15. x & 1 = x
16. x Ъ x = x
17. x Ъ ¬x = 1
18. x Ъ 0 = x
19. x Ъ 1 = 1
20. x Е y = ( x & ¬y ) Ъ ( ¬x & y )
21. x Й y = ¬x Ъ y
22. x є y = ( x & y ) Ъ ( ¬x & ¬y )

3 Двойственные функции

Определение 4 (Двойственная функция). Функция g ( x 1 . x n ) = ¬f ( ¬x 1 . ¬x n ) называется двойственной функцией к функции f и обозначается f * .

Пример 2 (двойственные функции).

( x & y ) * = ¬ ( ¬x & ¬y ) = x Ъ y .

Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f * ( x 1 . x n ) * = ( ¬f ( ¬x 1 . ¬x n )) * = *
= ¬¬f ( ¬¬x 1 . ¬¬x n ) = *
= f ( x 1 . x n ) *

Рассмотрим, что происходит с таблицей двойственной функции. Замена набора ( x 1 . x n ) на ( ¬x 1 . ¬x n ) соответствует «переворачиванию» таблицы. Действительно, наборы ( x 1 . x n ) и ( ¬x 1 . ¬x n ) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию ¬ к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Пример 3 (вектор двойственной функции).

Функции x & y и x Ъ y , задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являются x Е y и x є y , задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функций x и ¬x (векторы (0,1) и (1,0) соответственно) двойственна сама себе.

Теорема 1 (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее: f 0 ( f 1 . f m ) * = f 0 * ( f 1 * . f m * )

Доказательство. f 0 ( f 1 ( x 1 . x n ) . f m ( x 1 . x n )) * =

= ¬f 0 ( f 1 ( ¬x 1 . ¬x n ) . f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬¬f 1 ( ¬x 1 . ¬x n ) . ¬¬f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬f 1 * ( x 1 . x n ) . ¬f m * ( x 1 . x n )) =	*
= f 0 * ( f 1 * ( x 1 . x n ) . f m * ( x 1 . x n ))	*

4 Разложение функции по переменным

x s =

м ¬x, если s =0 н о x, если s =1

.

Теорема 2 (Разложение в дизъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m )

Доказательство. Покажем, что для любого набора значений переменных ( x 1 . x n ,x n+ 1 . x m ) значения левой и правой частей совпадают. Возьмём фиксированный набор ( x 1 . x n ,x n+ 1 . x m ). Рассмотрим выражение x 1 s 1 & . & x n s n . Если одно из значений x i s i равно 0, то и всё выражение равно 0. Тогда и выражение x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m ) равно 0. Единице же выражение x 1 s 1 & . & x n s n равно только в том случае, если s 1 = x 1 , . s n = x n . При этом f ( s 1 . s n ,x n+ 1 . x m ) = f ( x 1 . x n ,x n+ 1 . x m ) Таким образом, значение правой части всегда равно равно f ( x 1 . x m ), то есть значению левой части.

Теорема 3 (Разложение в конъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x n ¬ s n Ъ f ( s 1 . s n ,x n+ 1 . x m )

Разложения по всем переменным дают суперпозицию конъюнкции, дизъюнкции и отрицания.

Следствие 1 (Совершенная дизъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: *

f ( x 1 . x m ) = x 1 s 1 & . & x m s m & f ( s 1 . s m ) = *

= x 1 s 1 & . & x m s m

Следствие 2 (Совершенная конъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: * f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x m ¬ s m

Таким образом, любая булева функция может быть представлена суперпозицией конъюнкции, дизъюнкции и отрицания. Разложение по всем переменным в дизъюнкцию называется совершенной дизъюнктивной нормальной формой функции, а в конъюнкцию – совершенной конъюнктивной нормальной формой . *

Совершенная дизъюнктивная и конъюнктивная нормальная формы дают способ представления булевой функции через суперпозицию конъюнкции, дизъюнкции и отрицания если у нас есть таблица значений функции.

Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.

Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.

Пример 4 (совершенная дизъюнктивная нормальная форма).

Построим совершенную дизъюнктивную нормальную форму функции, заданной следующей таблицей.

x	y	z	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Наборы, на которых функция равна 1 – это (0,1,1), (1,0,1), (1,1,0), (1,1,1). Первый набор даёт конъюнкцию ¬x & y & z , второй – x & ¬y & z , третий – x & y & ¬z , четвёртый – x & y & z . В результате получаем ( ¬x & y & z ) Ъ ( x & ¬y & z ) Ъ ( x & y & ¬z ) Ъ ( x & y & z ).

Источник

Определение булевой функции

Определение:

Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики, англ. Boolean function) от [math]n[/math] переменных — отображение [math]B^n\rightarrow B[/math] , где [math]B = \<0, 1\>[/math] — булево множество.

Элементы булева множества [math]1[/math] и [math]0[/math] обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Элементы декартова произведения [math]B^n[/math] называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается [math]P_2[/math] , а от n переменных — [math]P_2(n)[/math] . Булевы функции названы так по фамилии математика Джорджа Буля.

Содержание

Основные сведения [ править ]

Определение:

А́рность (англ. arity) функции — количество ее аргументов.

Каждая булева функция арности [math]n[/math] полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины [math]n[/math] . Число таких векторов равно [math]2^n[/math] . Поскольку на каждом векторе булева функция может принимать значение либо [math]0[/math] , либо [math]1[/math] , то количество всех n-арных булевых функций равно [math]<2^2>^n[/math] . То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:

Таблица истинности
[math]x_1[/math]	[math]x_2[/math]	[math]\ldots[/math]	[math]x_n[/math]	[math]f(x_1,x_2,\ldots,x_n)[/math]
[math]0[/math]	[math]0[/math]	[math]\ldots[/math]	[math]0[/math]	[math]f(0,0,\ldots,0)[/math]
[math]1[/math]	[math]0[/math]	[math]\ldots[/math]	[math]0[/math]	[math]f(1,0,\ldots,0)[/math]
[math]0[/math]	[math]1[/math]	[math]\ldots[/math]	[math]0[/math]	[math]f(0,1,\ldots,0)[/math]
[math]1[/math]	[math]1[/math]	[math]\ldots[/math]	[math]0[/math]	[math]f(1,1,\ldots,0)[/math]
[math]\vdots[/math]	[math]\vdots[/math]	[math]\vdots[/math]	[math]\vdots[/math]	[math]\vdots[/math]
[math]0[/math]	[math]1[/math]	[math]\ldots[/math]	[math]1[/math]	[math]f(0,1,\ldots,1)[/math]
[math]1[/math]	[math]1[/math]	[math]\ldots[/math]	[math]1[/math]	[math]f(1,1,\ldots,1)[/math]

Практически все булевы функции малых арностей ( [math]0, 1, 2[/math] и [math]3[/math] ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable).

Нульарные функции [ править ]

При [math]n = 0[/math] количество булевых функций равно [math]<2^2>^0 = 2^1 = 2[/math] , первая из них тождественно равна [math]0[/math] , а вторая [math]1[/math] . Их называют булевыми константами — тождественный нуль и тождественная единица.

Унарные функции [ править ]

При [math]n = 1[/math] число булевых функций равно [math]<2^2>^1 = 2^2 = 4[/math] .

Таблица значений булевых функций от одной переменной:

Функции от одной переменной
[math]0[/math]	[math]x[/math]	[math]\neg x[/math]	[math]1[/math]
0	[math]0[/math]	[math]0[/math]	[math]1[/math]	[math]1[/math]
1	[math]0[/math]	[math]1[/math]	[math]0[/math]	[math]1[/math]
Сохраняет 0	✓	✓
Сохраняет 1	✓	✓
Самодвойственная	✓	✓
Монотонная	✓	✓	✓
Линейная	✓	✓	✓	✓

Названия булевых функций от одной переменной:

Обозначение	Название
[math]0[/math]	тождественный ноль, тождественная ложь, тождественное «НЕТ»
[math]x[/math]	тождественная функция, логическое «ДА», «YES»(англ.)
[math]\bar x,\ \neg x,\ x'[/math]	отрицание, логическое «НЕТ», «НЕ», «НИ», «NOT»(англ.), «NO»(англ.)
[math]1[/math]	тождественная единица, тождественная истина, тождественное «ДА», тавтология

Бинарные функции [ править ]

При [math]n = 2[/math] число булевых функций равно [math]<2^2>^2 = 2^4 = 16[/math] .

Таблица значений булевых функций от двух переменных:

Функции от двух переменных:
x	y	[math]0[/math]	[math]x \land y[/math]	[math]x \nrightarrow y[/math]	[math]x[/math]	[math]x \nleftarrow y[/math]	[math]y[/math]	[math]x \oplus y[/math]	[math]x \lor y[/math]	[math]x \downarrow y[/math]	[math]x = y[/math]	[math]\neg y[/math]	[math]x \leftarrow y[/math]	[math]\neg x[/math]	[math]x \rightarrow y[/math]	[math]x \triangledown y[/math]	[math]1[/math]
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Сохраняет 0		✓	✓	✓	✓	✓	✓	✓	✓
Сохраняет 1		✓	✓	✓	✓	✓	✓	✓	✓
Самодвойственная		✓	✓	✓	✓
Монотонная		✓	✓	✓	✓	✓	✓
Линейная		✓	✓	✓	✓	✓	✓	✓	✓

Названия булевых функций от двух переменных:

Обозначение	Другие обозначения	Название
[math]0[/math]	тождественный ноль, тождественная ложь, тождественное «НЕТ»
[math]x \land y[/math]	[math]x \cdot y,\ xy,\ x \And y,\ x\ AND\ y,\ AND(x, y),\ min(x, y), x [/math] И [math]y,[/math] И [math](x, y)[/math]	2И, конъюнкция
[math]x \nrightarrow y[/math]	[math]x \gt y,\ \neg(x \rightarrow y),\ x\ GT\ y,\ GT(x,\ y)[/math]	больше, инверсия прямой импликации
[math]x[/math]	[math]YES1(x,y),[/math] ДА1 [math](x, y)[/math]	первый операнд
[math]x \nleftarrow y[/math]	[math]x \lt y,\ \neg(x \leftarrow y),\ x\ LT\ y,\ LT(x, y)[/math]	меньше, инверсия обратной импликации
[math]y[/math]	[math]YES2(x, y),[/math] ДА2 [math](x, y)[/math]	второй операнд
[math]x \oplus y[/math]	[math]x + _2 y,\ x \not = y,\ x \gt \lt y,\ x \lt \gt y,\ x\ XOR\ y,\ XOR(x,y)[/math]	сложение по модулю 2, не равно, ксор, исключающее «или»
[math]x \lor y[/math]	[math]x + y,\ x\ OR\ y,\ OR(x,y),\ max(x,y),[/math] [math]x [/math] ИЛИ [math]y,[/math] ИЛИ [math](x, y)[/math]	2ИЛИ, дизъюнкция
[math]x \downarrow y[/math]	[math]x\ NOR\ y,\ NOR(x,y)[/math] [math]x [/math] ИЛИ-НЕ [math]y,[/math] ИЛИ-НЕ [math](x, y)[/math]	НЕ-2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса
[math]x = y[/math]	[math]x \equiv y, x EQV y, EQV(x,y), x \sim y, x \leftrightarrow y[/math]	равенство, эквивалентность
[math]\neg y[/math]	[math]NOT2(x, y),\ y’,\ \bar,[/math] НЕ2 [math](x, y)[/math]	отрицание (негация, инверсия) второго операнда
[math]x \leftarrow y[/math]	[math]x \geq y,\ x \subset y,\ x\ GE\ y,\ GE(x, y)[/math]	больше или равно, обратная импликация (от второго аргумента к первому)
[math]\neg x[/math]	[math]NOT1(x,y),\ x’,\ \bar,[/math] НЕ1 [math](x, y)[/math]	отрицание (негация, инверсия) первого операнда
[math]x \rightarrow y[/math]	[math]x \leq y,\ x \supset y,\ x\ LE\ y,\ LE(x,y)[/math]	меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму)
[math]x \triangledown y[/math]	[math]x \mid y,\ x\ NAND\ y,\ NAND(x,y),[/math] [math]x [/math] И-НЕ [math]y,[/math] И-НЕ [math](x, y)[/math]	НЕ-2И, 2И-НЕ, антиконъюнкция, Штрих Шеффера
[math]1[/math]	тождественная единица, тождественная истина, тождественное «ДА», тавтология

Тернарные функции [ править ]

При [math]n = 3[/math] число булевых функций равно [math]<2^2>^3 = 2^8 = 256[/math] . Некоторые из них определены в следующей таблице:

Таблица истинности некоторых тернарных функций
[math]x[/math]	[math]y[/math]	[math]z[/math]	[math]x \downarrow y \downarrow z[/math]	[math]\neg (\geq 2(x,y,z))[/math]	[math]x \not = y \not = z[/math]	[math]x \mid y \mid z[/math]	[math]min(x,y,z)[/math]	[math]x=y=z[/math]	[math]x \oplus y \oplus z[/math]	[math]\geq 2(x,y,z)[/math]	[math]f_1[/math]	[math]f_2[/math]	[math]max(x,y,z)[/math]
0	0	0	1	1	0	1	0	1	0	0	0	0	0
0	0	1	0	1	1	1	0	0	1	0	0	0	1
0	1	0	0	1	1	1	0	0	1	0	0	0	1
0	1	1	0	0	1	1	0	0	0	1	1	1	1
1	0	0	0	1	1	1	0	0	1	0	1	0	1
1	0	1	0	0	1	1	0	0	0	1	0	1	1
1	1	0	0	0	1	1	0	0	0	1	1	1	1
1	1	1	0	0	0	0	1	1	1	1	1	1	1

Названия булевых функций трех переменных:

Обозначения	Другие обозначения	Названия
[math]x \downarrow y \downarrow z[/math]	[math]\downarrow (x,y,z) = Webb_2 (x,y,z)[/math]	3-ИЛИ-НЕ, функция Вебба, функция Даггера, стрелка Пирса
[math]\neg (\geq 2(x,y,z))[/math]	Переключатель по большинству с инверсией, 3-ППБ-НЕ, мажоритарный клапан с инверсией
[math]x \not = y \not = z[/math]	[math][\not =(x,y,z)] = NE(x,y,z)[/math]	Неравенство
[math]x \mid y \mid z[/math]	[math]\mid(x,y,z)[/math]	3-И-НЕ, штрих Шеффера
[math]x \land y \land z[/math]	[math]\land (x,y,z) = (x\ AND\ y\ AND\ z) = AND(x,y,z) = min(x,y,z) = \lt br/\gt (x[/math] И [math] y[/math] И [math] z) = [/math] И [math](x,y,z)[/math]	3-И, минимум
[math]x=y=z[/math]	[math][=(x,y,z)] = EQV(x,y,z)[/math]	Равенство
[math]x \oplus y \oplus z[/math]	[math]x +_2 y +_2 z = \oplus (x,y,z) = +_2 (x,y,z)[/math]	Тернарное сложение по модулю 2
[math]\geq 2(x,y,z)[/math]	[math](x [/math] И [math]y) [/math] ИЛИ [math](y[/math] И [math] z)[/math] ИЛИ [math](z [/math] И [math] x)[/math]	переключатель по большинству, 3-ППБ, мажоритарный клапан
[math]f_1[/math]	Разряд займа при тернарном вычитании
[math]f_2[/math]	Разряд переноса при тернарном сложении
[math]x+y+z[/math]	[math]+(x,y,z) = max(x,y,z) = (x\ OR\ y\ OR\ z) = OR(x,y,z) = (x [/math] ИЛИ [math] y [/math] ИЛИ [math] z) = [/math] ИЛИ [math](x,y,z)[/math]	3-ИЛИ, максимум

Представление функции формулой [ править ]

Определение:

Если выбрать некоторый набор булевых функций [math]A[/math] , то с использованием выбранных функций можно записать некоторые другие булевы функции. Такая запись булевой функции называется формулой (англ. formula).

Например, если [math]A = \left\<\land,\neg\right\>[/math] , то функция [math]a \lor b[/math] представляется в виде [math]\neg(\neg a \land \neg b)[/math]

Тождественность и двойственность [ править ]

Определение:

Две булевы функции тождественны (англ. identical) друг другу, если на любых одинаковых наборах аргументов они принимают равные значения.

Тождественность функций f и g можно записать, например, так:
[math]f(x_1, x_2, \dots, x_n)=g(x_1, x_2, \dots, x_n)[/math]

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:

[math]\overline<0>=1[/math]	[math]\overline<1>=0[/math]	[math]\overline<\overline>=x[/math]	[math]x \land y=y \land x\![/math]	[math]x\lor y=y \lor x[/math]
[math]0 \land x=0\![/math]	[math]1 \land x=x\![/math]	[math]0 \lor x=x[/math]	[math]1\lor x=1[/math]	[math]x \land x=x \lor x=x[/math]

А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

[math]x \land \overline=0[/math]

[math]x \lor \overline=1[/math]

[math]\overline=\overline\lor\overline[/math]

[math]\overline\land\overline=\overline[/math]

(законы де Моргана)

[math]x \land (y\lor z)=(x \land y)\lor (x \land z)[/math]
[math]x \lor (y \land z)=(x\lor y) \land (x\lor z)[/math] (дистрибутивность конъюнкции и дизъюнкции)

Определение:

Функция [math]g(x_1,x_2,\dots,x_n)[/math] называется двойственной (англ. duality) функции [math]f(x_1,x_2,\dots,x_n)[/math] , если [math]f(\overline,\overline,\dots,\overline)=\overline[/math] .

Легко показать, что в этом равенстве [math]f[/math] и [math]g[/math] можно поменять местами, то есть функции [math]f[/math] и [math]g[/math] двойственны друг другу. Из простейших функций двойственны друг другу константы [math]0[/math] и [math]1[/math] , а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.

Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.

Суперпозиции [ править ]

Определение:

Суперпозиция функций, композиция функций (англ. function composition) — функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных.

Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.

Пусть нам дан некоторый набор булевых функций [math]K[/math] . Получить новую функцию, являющеюся композицией функций из [math]K[/math] , мы можем следующими способами:

• Подстановкой одной функции в качестве некоторого аргумента для другой;
• Отождествлением аргументов функций.

Полнота системы, критерий Поста [ править ]

Определение:

Замыкание множества функций (англ. сlosure) — подмножество всех булевых функций, что любую из этих функций можно выразить через функции исходного множества.

Определение:

Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций.

Американский математик Эмиль Пост [1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:

• функции, сохраняющие константу [math]T_0[/math] и [math]T_1[/math] ,
• самодвойственныые функции [math]S[/math] ,
• монотонные функции [math]M[/math] ,
• линейные функции [math]L[/math] .

Набор булевых функций [math]K[/math] является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов [math] S,M,L,T_0,T_1 [/math] , иными словами, когда в нем имеется хотя бы одна функция, не сохраняющая ноль, хотя бы одна функция, не сохраняющая один, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.

Представление булевых функций [ править ]

Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций [math]\Sigma = \[/math] . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре [math]\Sigma[/math] , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?
• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
  • В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Дизъюнктивная нормальная форма (ДНФ) [ править ]

Определение:

Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов.

Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.

[math]f(x,y,z) = (x \land y) \lor (y \land \neg )[/math] .

[math]f(x,y,z,t,m) = (x \land z) \lor (y \land x \land \neg) \lor (x \land \neg ) [/math] .

Конъюнктивная нормальная форма (КНФ) [ править ]

Определение:

Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.

[math]f(x,y,z) = (x \lor y) \land (y \lor \neg)[/math]

[math]f(x,y,z,t) = (x \lor t) \land (y \lor \neg) \land (\neg \lor \neg) \land (\neg \lor \neg \lor z)[/math]

[math]f(x,y,z,t,m) = (x \lor m \lor \neg) \land (y \lor \neg) \land (y \lor t \lor \neg)[/math]

Полином Жегалкина [ править ]

Определение:

Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида [math]0[/math] и [math]1[/math] , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или.

Полином Жегалкина имеет следующий вид:

[math]P = a_ <000\ldots000>\oplus a_ <100\ldots0>x_1 \oplus a_ <010\ldots0>x_2 \oplus \ldots \oplus a_ <00\ldots01>x_n \oplus a_ <110\ldots0>x_1 x_2 \oplus \ldots \oplus a_ <00\ldots011>x_ x_n \oplus \ldots \oplus a_ <11\ldots1>x_1 x_2 \ldots x_n [/math]

С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: [math]\bigl\langle \wedge, \oplus, 1 \bigr\rangle[/math] , который, в свою очередь, по теореме Поста является полным.

[math]f(x_1,x_2) = 1 \oplus x_1 \oplus x_1 x_2 [/math]

[math]f(x_1,x_2,x_3) = x_1 \oplus x_1 x_2 \oplus x_2 x_3 [/math]

[math]f(x_1,x_2,x_3,x_4) = 1 \oplus x_1 \oplus x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 x_2 x_4 [/math]

Тождественные функции. Выражение функций друг через друга [ править ]

Определение:

Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения.

Приведение тождественной функции есть выражение булевой функции через другие.

Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.

Пример:

Выразим следующие функции через систему функций [math]\ <\land, \lor, \lnot \>[/math] . [math] x \oplus y = \left ( x \land \lnot y \right ) \lor \left ( \lnot x \land y \right ) = \left ( x \lor \lnot y \right ) \land \left ( \lnot x \lor y \right )[/math] [math] x \downarrow y = \lnot \left ( x \lor y \right) = \lnot x \land \lnot y[/math] [math]\langle x, y, z \rangle = \left ( x \land y \right ) \lor \left ( y \land z \right ) \lor \left ( x \land z \right ) = \left ( x \lor y \right ) \land \left ( y \lor z \right ) \land \left ( x \lor z \right )[/math]

Подстановка одной функции в другую [ править ]

Определение:

Подстановкой (англ. substitution) функции [math]g[/math] в функцию [math]f[/math] называется замена [math]i[/math] -того аргумента функции [math]f[/math] значением функции [math]g[/math] : [math]h(x_<1>, \ldots, x_) = f(x_<1>, \ldots, x_, g(x_, \ldots, x_), x_, \ldots, x_)[/math]

Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.

При подстановке функции [math]g[/math] вместо [math]i[/math] -того аргумента функции [math]f[/math] , результирующая функция [math]h[/math] будет принимать аргументы, которые можно разделить на следующие блоки:

1. [math] x_<1>, \ldots, x_[/math]	— аргументы функции [math]f[/math] до подставленного значения функции [math]g[/math]
2. [math] x_, \ldots, x_ [/math]	— используются как аргументы для вычисления значения функции [math]g(y_<1>, \ldots, y_)[/math]
3. [math] x_, \ldots, x_ [/math]	— аргументы функции [math]f[/math] после подставленного значения функции [math]g[/math]

Пример:

Исходные функции: [math] f(a,b) = a \vee b [/math] [math] g(a) = \neg a [/math] [math] h(a,b) = f(a,g(b)) = a \vee \neg b [/math] — подстановка функции [math]g[/math] вместо второго аргумента функции [math]f[/math] . В данном примере при помощи подстановки мы получили функцию [math]h(a,b)=a \leftarrow b[/math] .

Отождествление переменных [ править ]

Определение:

Отождествлением переменных (англ. identification of variables) называется подстановка [math]i[/math] -того аргумента функции [math]f[/math] вместо [math]j[/math] -того аргумента: [math]h(x_<1>, \ldots, x_, x_, \ldots, x_) = f(x_<1>, \ldots, x_, \ldots, x_, x_, x_, \ldots, x_)[/math]

Таким образом, при отождествлении [math]c[/math] переменных мы получаем функцию [math]h[/math] с количеством аргументов [math]n-c+1[/math] .

Пример:

[math] f(a,b) = a \vee b [/math] — исходная функция [math] h(a) = a \vee a [/math] — функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию [math]P_<1>[/math] — проектор единственного аргумента.

Схемы из функциональных элементов [ править ]

Определение:

Схема из функциональных элементов, логическая схема (англ. logic diagram) — размеченный ориентированный граф без циклов, в некотором базисе [math]B[/math] , в котором:

1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);

2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса [math]B[/math] ). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса [math]B[/math] .

Отождествление переменных осуществляется при помощи ветвления проводников.

Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.

Некоторые логические элементы:

И	ИЛИ	НЕ	Штрих Шеффера	Стрелка Пирса

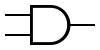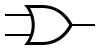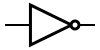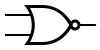Стандартный базис [ править ]

Определение:

Стандартный базис — система булевых функций: [math]\ <\land, \lor, \lnot \>[/math]

Если рассматривать множество бинарных булевых функций [math]P_2(2)[/math] , то для выражения любой булевой функции данного множества (кроме стрелки Пирса и штриха Шеффера) через стандартный базис достаточно выразить тождественные функции для эквиваленции, импликации и константы [math] 0 [/math] с использованием функций, принадлежащих стандартному базису, т. к. все остальные операции можно выразить через данные 3 функции с помощью отрицания:

[math] x \leftrightarrow y = \left ( x \rightarrow y \right ) \land \left ( y \rightarrow x \right ) [/math]

[math] x \rightarrow y = \lnot x \lor y [/math]

[math] 0 = x \land \lnot x [/math]

Функции [math] \mid \ и \downarrow[/math] являются отрицаниями функций [math] \land \ и \ \lor[/math] соответственно.

[math] x \mid y = \lnot \left ( x \land y \right )[/math]

[math] x \downarrow y = \lnot \left ( x \lor y \right )[/math]

Тождественность функций можно доказать с помощью таблицы истинности.

Выразим через стандартный базис обратную импликацию [math] \left (x \leftarrow y \right ) [/math] .

[math]x \leftarrow y = \lnot x \rightarrow \lnot y = x \lor \lnot y [/math]

Полнота стандартного базиса [ править ]

[math]\triangleright[/math] Данное утверждение — следствие теоремы об СДНФ. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. Способ выражения тождественного нуля через функции стандартного базиса уже был описан выше. [math]\triangleleft[/math]

[math] x \land y = \lnot \left (\lnot x \lor \lnot y \right ) [/math]

[math] x \lor y = \lnot \left (\lnot x \land \lnot y \right ) [/math]

Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:

[math] \ < \land , \lnot \>[/math] (конъюнктивный базис Буля)

[math] \ < \lor , \lnot \>[/math] (дизъюнктивный базис Буля)

Теоремы о числе функций в базисе [ править ]

Доказательство: [math]\triangleright[/math]

Рассмотрим произвольный безызбыточный базис [math] X[/math] . Тогда по теореме Поста [math]X[/math] содержит следующие функции (не обязательно различные):

[math]f_0 \notin T_0, f_1 \notin T_1, f_s \notin S, f_m \notin M, f_l \notin L[/math] , где [math] T_0, T_1, S, M, L[/math] — классы Поста.

Значит, так как [math]X[/math] — безызбыточный базис, а система [math]\[/math] — полная, то [math]\left | X \right | \le 5[/math]

Рассмотрим [math]f_0[/math] . Возможны два случая:

1. [math] f_0(1, 1, \ldots, 1) = 0 [/math] , тогда [math]f_0[/math] также не сохраняет единицу и немонотонная, т.е.

[math] f_0 = f_1 = f_m [/math] . Значит, [math]\left | X \right | \le 3[/math] .

2. [math] f_0(1, 1, \ldots, 1) = 1 [/math] , тогда [math]f_0[/math] несамодвойственная, т.е.

[math] f_0 = f_s [/math] . Значит, [math]\left | X \right | \le 4[/math] . [math]\triangleleft[/math]

Теорема:

Доказательство:

[math]\triangleright[/math]

Приведём примеры базисов для каждого [math]k[/math] : [math]k = 1 \Rightarrow X = \< \downarrow \>[/math] ; [math]k = 2 \Rightarrow X = \< \lnot, \land \>[/math] ; Докажем, что последняя система является базисом: Источник Читайте также:  Способы защиты головного мозга от ишемии при аневризме дуги аорты Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты