Баллистический способ измерения силы тяжести

Баллистический способ измерения силы тяжести

Среди динамических методов наиболее важными являются:

1. измерение периода колебаний маятника
2. измерение периода колебаний маятника под действием силы тяжести и силы, ей противодействующей
3. измерение времени свободного падения тел
4. измерение частоты колебаний струны, которая натянута подвешенной на ней массой.

Измерения силы тяжести бывают абсолютными и относительными.

При абсолютных измерениях определяют полную величину силы тяжести. При относительных – определяют не полное значение, а приращение в данном пункте относительно некоторого другого, исходного, поле в котором обычно известно.

Динамические методы могут быть как абсолютными, так и относительными. Статические – только относительными. Приборы, предназначенные для относительных определений силы тяжести, называют гравиметрами.

В настоящее время статические гравиметры являются основными приборами для относительных определений силы тяжести.

Математический маятник

Среди динамических методов измерения силы тяжести долгое время главенствовал маятниковый метод, доведенный до высокой степени совершенства.

Маятником называется любое твердое тело, способное совершать колебания около горизонтальной оси.

В теории колебаний важную роль играет модель математического маятника. Это идеальная модель, то есть модель, которую можно реализовать лишь в некотором приближении.

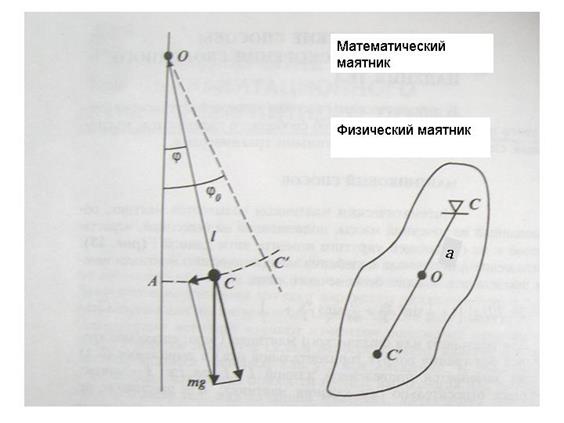
Математический маятник представляет собой материальную точку, с массой m, подвешенную на нерастяжимой и невесомой нити длиной l (рис18.1).

Дифференциальное уравнение движения имеет вид:

если задать начальные условия , , то его решением является гармоническая функция с периодом колебаний

Интеграл в этом выражении относится к классу эллиптических первого рода и не приводится к элементарным функциям. Обычно чтобы получить решение в явном виде, подынтегральную функцию разлагают в ряд (по φ), а затем почленно интегрируют. В нашем случае такая процедура приводит к выражению

Решение получается сложным, потому, что уравнение (18.1) является нелинейным. Однако при малых начальных отклонениях угла φ можно положить . Тогда уравнение (18.1) примет линейный вид:

Для него период колебаний равен

Как следует из этой формулы, при малых амплитудах период колебаний не зависит от амплитуды. Это свойство маятника называется изохронностью.

Поскольку математический маятник является идеальной моделью, ее, как правило, невозможно реализовать с необходимой степенью точности. Поэтому на практике при определениях силы тяжести используют физический маятник.

Физический маятник

Под физическим маятником понимают любое тяжелое твердое тело, свободно вращающееся вокруг горизонтальной оси.

Обозначим ось вращения как ось x (рис. 18.2).

Уравнение движения имеет вид:

здесь I_x– момент инерции, M_x – сумма моментов сил, ω – угловая скорость вращения.

Пусть центр тяжести маятника находится в точке C на расстоянии a от оси вращения O. Тогда сумма моментов действующих сил равна:

где M – масса тела. Тогда уравнение движения примет вид:

Если ввести новую переменную , то мы получим уравнение, аналогичное уравнению движения математического маятника (18.1):

Иными словами, физический маятник движется по тем же законам, что и математический. Только роль длины маятника играет величина .

Если эту величину отложить на рисунке, вдоль линии, соединяющей точку O и центр тяжести C, получим точку O’, которая называется центром качания, а длина l отрезка OO’ называется приведенной длиной физического маятника. Особенность положения центра качания в том, что физический маятник, подвешенный к нему будет качаться с тем же периодом.

Маятниковые приборы позволяют выполнять как абсолютные, так и относительные определения силы тяжести. При абсолютных определениях измеряют период колебания и приведенную длину маятника. При относительных определениях силы тяжести достаточно измерить только период колебания маятника в двух пунктах.

Действительно, пусть
тогда выражая значение силы тяжести на втором пункте, получим:

Маятниковые позволяют определить период колебаний с точностью , что обеспечивает точность измерения силы тяжести до 0.1 мГал. При этом время наблюдения на одном пункте составляет около 15 минут.

Баллистический метод

В настоящее время измерения малых интервалов и времени падения тел достиг очень высокой точности, поэтому появилась возможность высокоточных абсолютных измерений силы тяжести способом падающего груза, или баллистическим способом.

В вертикальной вакуумной камере высотой примерно 50 см в качестве падающего груза используется стеклянная призма (рис 18.3).

Путь падения призмы измеряют с помощью лазерного интерферометра, а время падения – с помощью атомных часов. Пучок когерентного света от лазера полупрозрачным стеклом разделяется на два пучка. Пучки света проходят разные пути, а затем сводятся вместе. В результате будет наблюдаться интерференционная картина в виде чередования темных и светлы полос (интерференционных полос), ширина и число которых зависят от спектрального состава источника света и разности оптических путей световых пучков.

Число полос N связано с разностью хода лучей Δ и длиной волны света λ соотношением

время и путь свободно падающего тела связаны соотношением

Однако на практике пользуются более сложной формулой

Это связано с тем, что в начале пути призма может получить небольшое дополнительное ускорение. Чтобы избавиться в выражении (18.12) от априорно неизвестной начальной скорости v₀ , измерения проводят дважды. Тогда из системы двух уравнений получим:

Точность абсолютных измерений баллистическим методом на сегодняшний день чрезвычайно высока – порядка одного микрогала (0.001 мГал) при времени одного измерения около 10 с. Для повышения точности выполняются многократные измерения, которые потом статически обрабатываются.

Источник

VIII Международная студенческая научная конференция Студенческий научный форум — 2016

МАЯТНИКОВЫЕ ПРИБОРЫ, БАЛЛИСТИЧЕСКИЕ И СТАТИЧЕСКИЕ ГРАВИМЕТРЫ

— динамические – тут наблюдают за движением тела в реальном гравитационном поле;

— статические — тут наблюдают за состоянием равновесия тела в реальном гравитационном поле под действием силы тяжести и некоторой компенсирующей силы.

К динамическим методам относятся:

— маятниковый основан на формуле Гюйгенса ( ),

где Т – период колебаний, g – ускорение силы тяжести, l – приведенная длина.

Маятниковый метод позволяет получить абсолютные значения ускорения силы тяжести с точностью порядка 0,1-0,3 мГал. Маятниковый метод в настоящее время, в основном, применяется для относительных измерений ускорения силы тяжести.

— баллистический основан на уравнении свободно падающего тела ( ),

где S – путь, пройденный свободно падающим телом, S_о – начальный путь, начальная скорость, t – время падения тела).

Баллистический метод – основной метод абсолютных измерений ускорения силы тяжести. Современные баллистические гравиметры являются стационарными и транспортабельными и представляют собой вакуумную установку, где свободно падает некоторое тело и с высокой точностью фиксируется путь, пройденный телом и время. Точность 0,01-0,02 мГал. Приборы – ГАБЛ ИАЭ, стационарная баллистическая установка в Севре .

По видам измерения ускорения силы тяжести делятся на: абсолютные (определяется полное значение силы тяжести), относительные (определяется приращение силы тяжести между двумя точками).

В зависимости от метода измерения гравиметры разделяются на статические и динамические. К статическим гравиметрам относится обширный класс приборов, основанных на принципе уравновешивания силы тяжести (или момента силы тяжести) упругой силой (или упругим моментом) чувствительного элемента.

Статические гравиметры используются только для относительных определений и являются основными приборами для измерения . Основной частью статического гравиметра является упругая система. Применяются системы типа пружинных весов, в которых мерой служат дополнительное растяжение пружины и линейное перемещение груза. Чаще используются крутильные системы, в которых маятник, подвешенный на горизонтальной упругой нити или пружине, поддерживается её упругой силой в положении, близком к горизонтальному. Мерой служит дополнительный поворот маятника или дополнительное усилие, необходимое для возвращения его в исходное (нулевое) положение. Системы такого типа в принципе нелинейны. При приближении маятника к положению неустойчивости резко возрастает чувствительность. Такая система называется астазированной.

Статические гравиметры применяются также для измерения в море на кораблях. При этом гравиметр помещается на гиростабилизированную платформу. В наблюдения вводятся поправки за вертикальные и горизонтальные возмущающие ускорения (измеряются специальными акселерографами) и за наклоны. Точность измерения на море на два порядка ниже, чем на суше. При помощи статического гравиметра проводятся опытные наблюдения на самолётах. Статические гравиметры широко применяются в гравиразведке.

К динамическим гравиметрам относятся струнные гравиметры и баллистические гравиметры. Струнные гравиметры применяются для относительных измерений. определяется по изменению частоты колебаний нагруженной струны. Баллистические гравиметры используются для абсолютных измерений измерений. Принцип действия баллистического гравиметра основан на измерении времени прохождения пробного (свободно падающего) тела через несколько точек, расстояния между которыми также измеряются. Высокая точность измерения достигается использованием кварцевых и атомных стандартов частоты и лазеров.

Источник

Динамические методы измерений силы тяжести

1. Маятниковый метод получил наиболее широкое распространение среди других динамических методов, применялся на практике в течение почти двух столетий и был доведен до высокой степени совершенства.

Маятником можно считать любое твердое тело, совершающее свободные колебания относительно горизонтальной оси. В теории метода рассматривают математический и физический маятники. Математический маятник представляет собой материальную точку с массой m, подвешенную на абсолютно нерастяжимой и невесомой нити длиной ℓ(рис. 2.10). Угол φ_о соответствует максимальному отклонению маятника от положения равновесия и называется амплитудой колебаний. Время, необходимое маятнику для прохождения от одного крайнего положения +φ_о до другого крайнего положения -φ_о, называется периодом колебаний Т маятника. Дифференциальное уравнение движения математического маятника имеет вид:

d 2 φ/dt 2 = — (g/ℓ) sin φ (2.36)

Рис. 2.10. Математический и физический маятники.

Решение этого уравнения дается в виде:

(2.37)

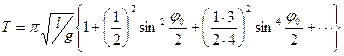
Как видно из последнего равенства, период зависит от амплитуды. При малых амплитудах, когда можно считать sin φ = φ, период колебаний маятника не зависит от амплитуды (это свойство маятника называется изохронностью) и равенство (2.37) приобретает вид формулы Гюйгенса:

, (2.38)

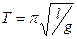
Обычно при гравиметрических измерениях амплитуда колебаний маятника не превышает 1 о , поэтому условие sin φ = φ практически выполняется и из формулы (2.38) получим:

.(2.39)

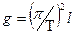
На практике осуществить математический маятник с необходимой степенью точности невозможно. Поэтому при измерениях силы тяжести используют физический маятник, который, имея определенные размеры, не является точечным и нить подвеса не является абсолютно нерастяжимой и невесомой. Уравнение движения физического маятника можно записать так:

, (2.40)

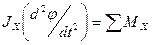
где J_X и M_X – соответственно момент инерции и момент сил относительно оси вращения Х.

Поскольку сумма моментов действующих сил:

, где М – масса тела, то уравнение движения принимает вид:

(2.41)

, (2.42)

(2.43)

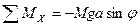
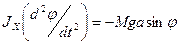
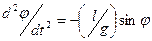
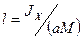
Выражение (2.42) совпадает с дифференциальным уравнением колебания математического маятника, т. е. физический маятник колеблется по тем же законам, что и математический, но роль длины l для него играет величина J_X/(aM), называемая приведенной длиной физического маятника.

Обычно приведенную длину физического маятника трудно определить с достаточной точностью, например, для маятника с приведенной длиной l = 100 см (Т ≈ 1с) при заданной погрешности измерения ускорения силы тяжести 0,1 мГл период колебаний и длину надо измерять с допустимыми погрешностями соответственно 3,5 10 -8 с и 0,07 мкм (Огородова, Шимбирев, Юзефович, 1978). Поэтому для определения абсолютных значений g использовали специальные оборотные маятники. Абсолютное значение силы тяжести необходимо знать хотя бы в одной точке. В настоящее время таким пунктом является Потсдамский геодезический институт, к которому отнесены все гравиметрические съемки мира. Здесь определение абсолютного значения силы тяжести было проведено под руководством Гельмерта в 1898 -1904 г.г. На основании 192 определений получено абсолютное значение силы тяжести 981 274 ±3 мГл.

При современном состоянии техники точность этого метода не может быть повышена из-за ряда трудно учитываемых факторов: удлинения маятника под действием собственного веса, деформации опор, неточности измерения приведенной длины и др.

Маятниковым методом проводили и относительные измерения (если в одном из пунктов известно полное значение силы тяжести g₁). В последнем случае, если измерить периоды качания маятника в двух пунктах Т₁ и Т₂ , то, учитывая формулу (2.38):

, откуда следует (2.44)

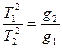
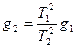
Гравиметры для относительных измерений силы тяжести применялись для создания опорных гравиметрических сетей и обеспечивали погрешности определения относительных значений силы тяжести около 0,1 мГл при весе порядка 90 кг и цикле одного измерения 15 – 20 мин. Однако в последнее время они были вытеснены приборами, основанными на баллистическом способе измерений.

2. Баллистический метод основан на зависимости времени падения тел в вакууме (t) от значения силы тяжести (g):

, откуда , (2.45)

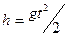
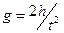
где h — высота, с которой падает объект при нулевой начальной скорости.

Из-за требований высокой точности определения величин h и t , только в 60-х годах 20 века, с применением лазерной техники, появилась возможность конструировать приборы для измерения силы тяжести этим методом. Кроме того, как было установлено, величины h и t нельзя отсчитывать от начала падения, так как при освобождении тело может получить дополнительное ускорение. Наиболее приемлемым оказалось бросать тело вверх и измерять время, за которое тело проходит определенный участок пути при подъеме и падении.

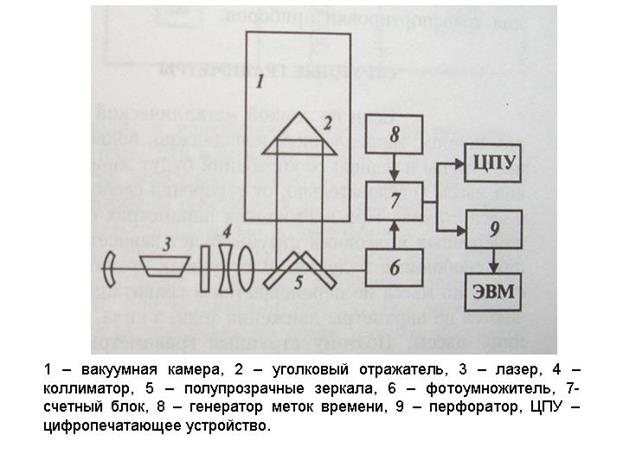
Рис. 2.11. Схема баллистического интерферометра для определения

абсолютных значений силы тяжести.

В этом случае формула для расчета значения g достаточно проста:

, (2.46)

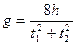
где t₁ и t_{2 —} промежутки времени между пересечениями телом специальных щелей при движении его вверх и вниз.

В различных странах за рубежом разработаны и применяются несколько типов баллистических гравиметров. Почти все они представляют собой экспериментальные образцы. В Сибирском отделении АН РФ разработан баллистический гравиметр, в котором применяется интерферометр Майкельсона с газовым лазером (рис. 2.11). В вакуумной камере 1 падает уголковый отражатель 2, ориентируемый по вертикали в крайнем верхнем положении при помощи агатовой опоры. Оптическая система интерферометра содержит стабилизированный лазер 3, коллиматор 4. полупрозрачные зеркала 5, делящие луч на две части, и фотоумножитель 6. В счетном блоке осуществляется измерение пути и времени. Величина h определяется по числу интерференционных полос, образованных при наложении прямого и обратного луча лазера от падающего уголкового отражателя. Для обработки результатов используется компьютер.

Один цикл измерения – подъем и падение уголкового отражателя, а также обработка результата – занимает около 12 с. За один час, включая паузы, можно сделать около 200 циклов. За несколько часов может быть достигнута точность в несколько сотых мГл. Для достижения точности выше 0,01 мГл наблюдения ведутся сутками (Огородова, Шимбирев, Юзефович, 1978). Полный комплект установки имеет массу в несколько сотен килограммов, но разделяется на отдельные транспортабельные части. Баллистические гравиметры-интерферометры используются сейчас для геодезических измерений и для создания опорных гравиметрических сетей.

3. Струнный метод основан на измерениях собственных поперечных колебаний струны, натянутой грузом. Если подвесить массу на тонкой металлической нити (струне), то натяжение струны и соответственно период колебаний будут зависеть от веса массы, длины и веса струны. При постоянных параметрах струны и груза изменения силы тяжести проявляются в изменении частоты колебаний струны.

Частота колебаний (f) идеально гибкой струны определяется:

, (2.47)

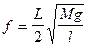
где L — длина струны, M — масса груза, подвешенного на струне, — линейная плотность струны (г/см). Отсюда:

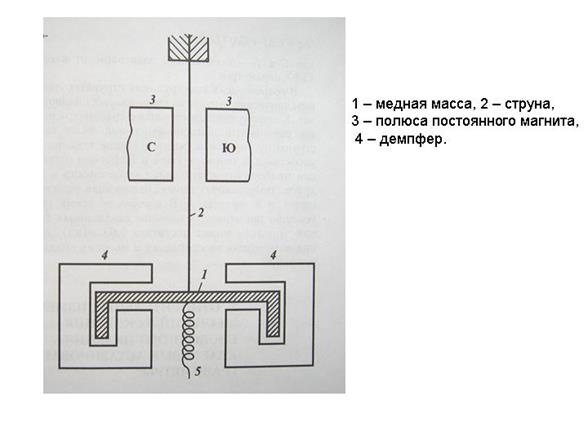
Рис. 2.12. Общая схема устройства струнного гравиметра

.(2.48)

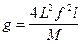
Этот принцип в абсолютных измерениях не используется из-за сложностей определения эффективной длины реальной струны.

Для относительных измерений используется схема, приведенная на рис. 2.12. Груз 1 подвешен на струне 2, проходящей между полюсами постоянного магнита 3, поэтому колебания струны приводят к возникновению в ней переменного тока. Чтобы ток не затухал, струна включена в контур с положительной обратной связью, образуя струнный генератор.

Частота струнного генератора умножается и сравнивается с частотой эталонного генератора. Для устранения продольных колебаний струны применяется электромагнитное демпфирование при помощи постоянных магнитов 4, возможность маятниковых колебаний ограничивают плоские горизонтальные пружины.

Изменение напряженности поля Δg связано с изменением частоты колебаний струны Δf квадратичной зависимостью:

, (2.49)

, (2.50)

, (2.51)

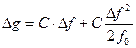
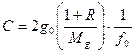
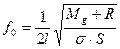
M — масса груза, l – длина струны, σ – плотность материала струны, S – площадь поперечного сечения струны, R – величина, зависящая от параметров вспомогательных пружин.

Поскольку точное измерение величин, определяющих коэффициент С, является сложной задачей, здесь применяют способы градуирования, которые используются в статических гравиметрах (см. ниже).

Достоинства струнного гравиметра – практически неограниченный диапазон измерения и малая зависимость частоты колебаний струны от температуры, а также простота измерений и цифровой регистрации. Недостатки струнного гравиметра – слабая устойчивость к влиянию вибраций и других инерционных помех, а также нелинейная зависимость между Δg и f.

Струнные гравиметры применяют для измерений в скважинах и иногда – на самолетах и морских судах.

Источник