Атд словарь способы реализации словаря

§14. Реализация атд «Словарь». Хеширование.

Применение множеств при разработке алгоритмов не всегда требует таких мощных операторов, как операторы объединения и пересечения. Часто достаточно только хранить в множестве «текущие» объекты с периодической вставкой или удалением некоторых из них. Время от времени также возникает необходимость узнать, присутствует ли конкретный элемент в данном множестве.

Абстрактный тип множеств с операторами , и называется 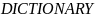(Словарь).

Также, стоит включить оператор 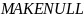в набор операторов словаря — он потребуется при реализации АТД для инициализации структур данных. Рассмотрим реализации, наиболее подходящие для представления таких словарей.

Словари можно представить посредством сортированных или несортированных связанных списков, двоичных векторов или массивов фиксированной длины с указателем на последнюю заполненную ячейку этого массива. Эти реализации уже были рассмотрены в §13.

Существует еще один полезный и широко используемый метод реализации словарей, который называется хешированием. Этот метод требует фиксированного времени (в среднем) на выполнение операторов и снимает ограничение, что множества должны быть подмножествами некоторого конечного универсального множества. В самом худшем случае этот метод для выполнения операторов требует времени, пропорционального размеру множества, так же, как и в случаях реализаций, посредством массивов и списков. Но при тщательной разработке алгоритмов можно добиться, что вероятность выполнения операторов за время, большее фиксированного, будет как угодно малой.

Рассмотрим две различные формы хеширования. Одна из них называется открытым, или внешним хешированием и позволяет хранить множества в потенциально бесконечном пространстве, снимая тем самым ограничения на размер множеств. Другая называется закрытым, или внутренним хешированием и использует ограниченное пространство для хранения данных, ограничивая, таким образом, размер множеств.

1. Открытое хеширование

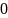
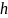
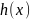
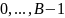
На рис. 14.1 показана базовая структура данных при открытом хешировании. Основная идея заключается в том, что потенциальное множество (возможно, бесконечное) разбивается на конечное число классов. Для классов, пронумерованных от до , строится хеш-функция такая, что для любого элемента х исходного множества функция принимает целочисленное значение из интервала , которое, естественно, соответствует классу, которому принадлежит элемент .

Элемент называют ключом, — хеш-значением , а «классы» — сегментами. Будем говорить, что элемент принадлежит сегменту .

Рис. 14.1 Организация данных при открытом хешировании

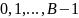
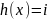
Массив, называемый таблицей сегментов и проиндексированный номерами сегментов , содержит заголовки для списков. Элемент -ro списка — это элемент исходного множества, для которого .

Если сегменты примерно одинаковы по размеру, то в этом случае списки всех сегментов должны быть наиболее короткими при данном числе сегментов. Если исходное множество состоит из элементов, тогда средняя длина списков будет 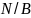элементов. Если можно оценить величину и выбрать как можно ближе к этой величине, то в каждом списке будет один-два элемента. Тогда время выполнения операторов словарей будет малой постоянной величиной, не зависящей от (или, что эквивалентно, от ).

Не всегда ясно, как выбрать хеш-функцию так, чтобы она примерно поровну распределяла элементы исходного множества по всем сегментам. Далее будет показан простой способ построения функции , причем будет «случайным» значением, почти независящим от .

Пример 1. Введем хеш-функцию (которая будет «хорошей», но не «отличной»), определенную на символьных строках. Идея построения этой функции заключается в том, чтобы представить символы в виде целых чисел, используя для этого машинные коды символов.

Пусть каждый ключ x является строкой, состоящей не более, чем из 10 символов. А – множество всех ключей. Тип ключа в Pascal можно определить так

nametype=array [1..10] of char

Встроенная функция ord(c) в языке Pascal возвращает целочисленный код символа с. Для любого х∈А зададим хеш-функцию так, что

mod B

– остаток от деления на B суммы целочисленных кодов всех символов строки x.

Например, если x=abc, то h(x)=(ord(a)+ord(b)+ord(c))mod B.

Источник

Словарь на упорядоченном массиве

Словарь на массиве

П усть перед нами стала задача хранить пары . Такая задача встречается очень часто. Например, нужно хранить информацию о продукте по его id, медиа-данные по их метаданным, изображение по его имени, информацию о человеке по его имени и фамилии и т.д.

Такой контейнер должен, по крайней мере, реализовывать операции

• PUT(ключ, значение) – для вставки новой пары в контейнер. При этом поведение в случае вставки значения, которое уже есть в коллекции, не определено. Можно подменять старое значение, либо выбрасывать ошибку, либо ничего не делать.
• GET(ключ) – для получения значение по ключу. Здесь не определено, что будет возвращаться в случае, если такого значения в коллекции нет. Например, если мы храним указатель, то можно возвращать NULL. Но вполне возможно, что NULL – это приемлемое значение для указателя. Также NULL, если ключ целочисленный, может трактоваться, как число 0.
• REMOVE(ключ) – для удаления пары из контейнера. Во время удаления объект изымается из контейнера, но дальнейшее поведение опять не определено. Удалять пару может как функция REMOVE, так и внешняя функция, получившая результат.

Кроме того, хотелось бы иметь возможность перебрать все значения из коллекции, а также находить максимальное и минимальное значения.

Самое простое решение использовать неупорядоченный массив структур. Очевидно, что в таком случае вставка будет иметь сложность порядка 1, поиск порядка n, так как придётся перебрать все элементы, удаление также потребует n шагов, потому что перед удалением нужно найти пару в массиве (само удаление будет иметь сложность 1).

Коллекция «словарь» использует для хранения упорядоченный по ключу массив пар. Соответственно, поиск всегда будет иметь сложность log(n), так как в упорядоченном массиве можно использовать двоичный поиск. Удаление и вставка будет иметь сложность порядка n, так как придётся сдвигать элементы массива (делать это, конечно, будем не в цикле, а функцией memcpy).

Очевидно, что такая структура может быть использована в том случае, когда вставки и удаления производятся нечасто. Например, мы выгружаем данные в контейнер, а затем работаем с ним, как с локальным хранилищем.

В то же время, поиск максимального и минимального по ключу значений будет иметь сложность 1, так как это будут крайние элементы массива.

Так как массив структур упорядочен, то необходимо, чтобы для ключей были реализованы, как минимум, две функции – сравнения на равенство и сравнения на больше (или меньше).

Реализация

К ак обычно, массив структур будет иметь некоторый начальный размер, чтобы не утруждаться частым изменением размера. Сделаем значение по умолчанию равным 100.

Для начала определим новые типы данных. Первый для ключа, он будет называться K, второй для значения V (Key и Value). В нашем примере ключом и значением будет строка.

Далее, необходимо определить функции для работы с нашими ключами. Первым делом – сравнение на равенство и меньше

Так как у нас уже имеются меньше и равно, то больше может быть через них выражено.

Функция freeEntry будет использоваться для освобождения памяти из-под пары. Так как ключом и значением могу являться, в принципе, любые объекты, для которых определены операции сравнения, то и их удаление может происходить разными способами.

Мы уже говорили о том, что словарь будет иметь какой-то начальный размер. В том случае, если число элементов превысит размер, то необходимо будет изменять размер массива. Новый размер предлагается вычислять как старый, умноженный на некоторое число multiplier. Поэтому введём две константы – начальный размер и множитель.

Сама структура словарь

Здесь data – массив указателей на пары. Изначально у нас будет только массив указателей на пары. При вставке новой пары элемент массива будет хранить адрес новой пары.

size – количество элементов в словаре. multiplier – множитель, во сколько раз изменится размер массива при превышении размера.

limit – размер массива.

Функция, создающая новый пустой словарь

Самая важная функция – поиск элемента. В двоичном поиске мы находим элемент в упорядоченном массиве. Если его нет, то возвращаем, например, указатель на NULL, если нашёлся, то указатель на элемент. Наша функция должна определять, есть ли элемент в массиве. Если он есть, то возвращать его индекс, а также указывать, что элемент был найден. Если элемента нет, то указать, что элемент не найден, и вернуть индекс элемента, после которого нужно производить вставку (или до какого элемента производить вставку). Поиск осложняется ещё и тем, что индекс имеет тип size_t, то есть не может стать отрицательным. При вычитании из size_t единицы получим большое целое число.

Наша функция будет возвращать 0, если элемент не найден и 1, если найден. Также она будет присваивать переданному через указатель параметру индекс найденного элемента, либо индекс, после которого нужно производить вставку. В идеале.

• 1. Представим, что мы ищем элемент, который меньше самого маленького элемента массива. Тогда функция возвратит 0, а значение index будет равно 0. По идее, оно должно быть отрицательным, так как мы хотим позицию, после которой нужно вставлять элементы. Таким образом, эту проблему мы перекладываем на вызывающую функцию, которая должна с ней как-то рабираться.
• 2. Мы ищем элемент в массиве длиной 0. Тогда j-1 приведёт к тому, что j станет очень большим, попытается провести поиск в пустом массиве и наткнётся на access violation. Опять же, перекладываем проблему на вызывающую функцию.
• 3. Мы ищем последний элемент. Если он есть, то будет возвращена единица и индекс, указывающий на него. Но тот же самый индекс будет возвращён и в случае, ели такого элемента нет. Снова этот случай пусть рассматривает вызывающая функция.

Наша функция вставки пары. put_raw возвращает 0, если элемент уже содержится, и 1, если произошла вставка.

Рассмотри подробнее. Первый блок.

Ситуация, когда элемента нет. Обрабатываем её отдельно. Далее ищем элемент.

Если такой элемент уже содержится, то выходим из функции и возвращаем ноль. Далее необходимо проверить размер массива. Если он превышен, то нужно изменить его размер.

А вот теперь рассматриваем оставшиеся исключительные ситуации. Получили индекс последнего элемента массива.

Или индекс, равный 0.

Оканчивается всё одинаково

Теперь нужна обёртка, чтобы можно было вставить ключ и значение.

Здесь создаётся новая пара. Заметьте, что если вставку не удалось произвести, то нужно будет удалить переданную пару, иначе будет утечка памяти.

Здесь также есть особая ситуация, когда размер словаря равен нулю. Обратите внимание на memcpy: необходимо проверять, чтобы мы не скопировали 0 байт. Такая ситуация произойдёт в том случае, если index равен размеру, то есть когда удаляем последний элемент. В этом случае index+1 выйдет за пределы массива, и даже не смотря на то, что размер копируемой области равен 0, вылетит ошибка.

Функция получения значения пары по ключу

Здесь мы решаем проблему возвращаемого значения следующим образом. Если элемент найден, то wasFound будет равняться 0, даже если значения элемента равно NULL.

Последняя из основных функция – удаление словаря.

Поиск максимального и минимального элементов

Обратите внимание, что поиск минимального и максимального элементов производится по ключам! Для поиска экстремального значения нужно будет пройти по всем элементам.

Источник

Способы представления словарей для автоматической обработки текстов

Автоматический анализ текстов практически всегда связан с работой со словарями. Они используются для морфологического анализа, выделения персон (нужны словари личных имен и фамилий) и организаций, а также других объектов.

В общем виде словарь — множество записей вида <строка, данные ассоциированные с этой строкой>.

Например, для морфологического анализа словарь состоит из троек <словоформа, нормальная форма, морфологические характеристики>. При анализе слова «мыла» из предложения «мама мыла раму» надо уметь получать следующие варианты анализа:

Нормальная форма	Характеристики
МЫЛО	S (существительное), РОД (родительный падеж), ЕД (единственное число), СРЕД (средний род), НЕОД (неодушевленность)
МЫЛО	S (существительное), ИМ (именительный падеж), МН (множественное число), СРЕД (средний род), НЕОД (неодушевленность)
МЫЛО	S (существительное), ВИН (винительный падеж), МН (множественное число), СРЕД (средний род), НЕОД (неодушевленность)
МЫТЬ	V (глагол), ПРОШ (прошедшее время), ЕД (единственное число), ИЗЪЯВ (изъявительное наклонение), ЖЕН (женский род), НЕСОВ (несовершенный вид)

Хеш-таблицы

На первый взгляд все просто. Надо использовать хеш-таблицу и дело с концом. Когда словарь маленький это решение очень просто и эффективно.

Однако, например, морфологический словарь русского языка содержит около 5 млн. словоформ. Получается, что:

• Надо хранить эти 5 млн. словоформ
• Для каждой словоформы должна быть ссылка на множество наборов морфологических характеристик
• Для каждой словоформы хранить ее начальную форму

Такой способ организации данных является неэкономным, поскольку, во-первых, слова склоняются в основном регулярно, и, во-вторых, в случае русского языка в рамках одного словарной статьи можно выделить подгруппы словоформ, в которых сама форма изменяется незначительно, или не изменяется совсем.

Например, слово «стена»:

• ед. ч: «стена»[им], «стены»[род], «стене»[дат], «стену»[вин], «стеной»[твор], «стеною»[твор], «стене»[предл];
• мн. ч: «стены»[им], «стен»[род], «стенам»[дат], «стены»[вин], «стенами»[твор], «стенах»[предл].

Видно, что изменяется только окончание, но в хеш-таблице надо хранить слово целиком.

Можно раздельно храненить основы (неизменяемых частей) и окончания, но в этом случае усложняется проверка слова.

От префиксного дерева к конечным автоматам

Для ясности примеров будем рассматривать более простую задачу, когда для каждой словоформы при анализе надо получать только ее морфологические признаки. Как хранить нормальную форму будет описано в конце.

По сравнению с хеш-таблицами, более компактным представлением является префиксное дерево (trie):

Важное замечание — на рисунках не будут показываться наборы признаков, ассоциированные с каждым конечным узлом дерева (или состоянием конечного автомата). Например, на рисунке узел 6, куда мы попадем по строке «стены» на самом деле будут 3 разбора:

• единственное число, родительный падеж;
• множественное число, именительный падеж.;
• множественное число, винительный падеж.

Префиксное дерево можно рассматривать как конечный автомат.

В автомате есть три вида состояний:

• Начальные — те, с которых начинается работа с автоматом. В детерминированном автомате такое состояние одно, но в недетерминированном их может быть несколько. На рисунках это крайнее левое состояние с номером 0.
• Финальные — такие состояния, достижение которых означает, что такое слово в словаре есть. Они обозначаются двойным кругом
• Простые состояния, которые не являются ни начальными, ни финальными

В дальнейшем будут использоваться обозначения:

• строка обозначается как w
• w[i] — i-тый символ данного слова (начиная с 0).
• s[i] — i-тый узел дерева (или состояние автомата), состояния нумеруются неотрицательными целыми числами, так же будем считать, что s[0] — начальное состояние.
• s[i][j] — переход из состояния s[i] по символу j. Считаем, что если переход есть, то такое выражение вернет номер состояния, если нет — то вернет -1.

Приведу базовые алгоритмы для префиксного дерева/конечного автомата.:

Представление префиксного дерева как конечного автомата обладает важными свойствами:

• такой автомат детерминирован — из каждого состояния возможно не более одного перехода по некоторому символу
• в нем нет циклов — при любом способе обхода автомата никакое состояния не посещается более одного раза.

Такой специальный автомат называется DAFSA (deterministic acyclic finite state automaton).

Надо сделать еще одно важное замечание. Для удобства представления и для практического использования будем считать, что состояние описывается не только таблицей переходов, но и данными о финальности состояния. И будем считать, что состояние финально, если в нем такие данные есть, и нет — если они отсутствуют.

Минимальные конечные автоматы

Использование префиксных деревьев позволяет избавиться от избыточности префиксов. Фактически это означает, что сокращается объем для хранения неизменяемой части слова. Однако, например, в русском языке окончания слова изменяются в основном регулярно.

Например, слова «стрела» и «стена» изменяются одинаково:

СТЕНА: ед. ч: «стена»[им], «стены»[род], «стене»[дат], «стену»[вин], «стеной»[твор], «стеною»[твор], «стене»[предл]; мн. ч: «стены»[им], «стен»[род], «стенам»[дат], «стены»[вин], «стенами»[твор], «стенах»[предл].

СТРЕЛА: ед. ч: «стрела»[им], «стрелы»[род], «стреле»[дат], «стрелу»[вин], «стрелой»[твор], «стрелою»[твор], «стреле»[предл]; мн. ч: «стрелы»[им], «стрел»[род], «стрелам»[дат], «стрелы»[вин], «стрелами»[твор], «стрелах»[предл].

Видно, что состояния 4 и 17, с которых начинаются окончания, у обоих слов эквивалентны. Очевидно, что слов с одинаковыми правилами словоизменения в словаре будет много. А значит можно существенно сократить число состояний.

Собственно, в теории автоматов есть понятие о минимальном автомате – таком автомате, который содержит минимально возможное число состояний, но был бы эквивалентен данному.

Например, для приведенного выше автомата, минимальный выглядит вот так:

Существуют и алгоритмы минимизации конечных автоматов, но все они обладают существенным недостатком — для их работы необходимо построить сначала неминимизированный автомат.

Другим, менее очевидным недостатком, является то, что построенный минимальный автомат не так просто изменять. К нему не подходит простая процедура добавления нового слова, которая используется для префиксного дерева.

Например, мы построили автомат для слов «fox» и «box», а потом минимизировали его.

Если в этот автомат добавить без полного перестроения слово «foxes», то получится следующая картина:

Получается, что в месте с «foxes» добавилось и «boxes», которое мы не добавляли.

В результате схема использования классических алгоритмов минимизации следующая: при любом изменении словаря необходимо:

• Построить префиксное дерево (или дополнительно хранить)
• Минимизировать автомат

Если словарь большой, то эти процедуры могут занимать значительное время и объем памяти.

Инкрементальная минимизация детерминированных ацикличных конечных автоматов

Решение трудностей с минимизацией автоматов представлено в работе: Jan Daciuk; Bruce W. Watson; Stoyan Mihov; Richard E. Watson. «Incremental Construction of Minimal Acyclic Finite-State Automata». В ней представлен алгоритм инкрементальной минимизации детерминированных ацикличных конечных автоматов. Он позволяет изменять уже построенный минимальный автомат. В результате не надо строить полный автомат, а затем его минимизировать.

Опять рассмотрим наш автомат СТЕНА+СТРЕЛА:

Важным понятием алгоритма является «состояния строки» — это последовательность состояний, которая получается при обходе автомата по заданной строке.

Например, при обходе строки «стрелой» получим следующую последовательность состояний [0, 1, 2, 14, 15, 4, 9, 10].

Другим важным понятием этого алгоритма является число переходов в заданное состояние (confluence). Если число переходов более одного, то изменять такое состояние небезопасно. На рисунке это состояние 4: у него 2 входящие стрелки.

Кроме того, алгоритм предполагает, что существует реестр состояний, который позволяет быстро получить состояние, равное данному.

В результате алгоритм добавления слова w выглядит так:

Иллюстрация работы алгоритма

Рассмотрим простой случай, когда финальность состояние — бинарный признак. Состояние или финально, или нет.

Автомат для строки «fox».

Видно, что автомат минимальный, в реестре находятся все состояния [0,1,2,3]

Добавим к нему слово «box». Поскольку у них нет общего префикса, то добавляем всю строку как суффикс. В результате получим:

Можно заметить что состояния 3 и 6 равны. Заменим 6 на 3:

Теперь видно, что равны 2 и 5. Заменим 5 на 2:

А теперь видно, что равны 1 и 4. Заменим 4 на 1:

Добавим строку «foxes». При вычислении префикса нашли, что состояния [0, 1, 2, 3] — путь префикса.
Кроме того, обнаружили, что в состояние 1 входит более одного перехода. Как результат — надо клонировать состояния 1, 2 и 3 по пути обхода слова «fox», поскольку если просто добавить «foxes» к предыдущему автомату, то будет распознаваться строка «boxes», которую мы не задавали.

Теперь добавим «boxes»:

При добавлении «boxes» автомат стал меньше. Это на первый взгляд неожиданное поведение, когда при добавлении новых строк автомат в действительности уменьшается. Есть и обратное поведение — когда при удалении строки автомат увеличивается.

Для правильной работы алгоритма важно корректно реализовать работу с реестром. Состояние удаляется из реестра при любом его изменении таблицы переходов состояния и признака финальности.

Кроме того, в отличие от обычного множества или таблицы, в добавление/удаление из реестра оперирует точно этим состоянием, а запрос делается на равное.

Практические использование

Представленный алгоритм используется в проекте АОТ и в системе ЭТАП-3 для организации быстрого морфологического анализа. При использовании конечных автоматов достигается скорость анализа порядка 1-1.5 млн. слов в секунду. При этом размер автомата без особых ухищрений умещается в 8 Мб.

Ранее описывалось хранение данных строки как признак финальности. Рассмотрим этот подход более подробно.

Хранение данных в состоянии автомата

Подход предполагает, что данные строки рассматриваются как некий атомарный объект. Это в свою очередь накладывает ограничения на эффективность минимизации автомата.

Например, процедура построения минимального автомата бессмысленна для идеального хеширования, когда со строкой ассоциировано уникальное число. Потому что в этом случае каждый суффикс будет уникальным, и соответственно, минимизации не будет, поскольку каждое финальное состояние уникально.

Для морфологического анализа в качестве ассоциированных данных можно использовать наборы морфологических характеристик. Это хорошо работает, поскольку таких наборов мало относительно общего количества словоформ. Например в русском языке в зависимости от принятой модели число таких наборов 500-900. А словоформ 4-5 млн.

Однако, эффективность минимизации сходит на нет, если в добавок к характеристикам сохранять и полную нормальную форму. Это происходит потому, что пара <нормальная форма, морфологические характеристики>практически уникальна.

В системе ЭТАП-3 используется именно такой подход для хранения морфологической информации. В самом автомате хранятся только наборы морфологических признаков. А для хранения нормальной формы используется следующий трюк. На этапе построения автомата в качестве входного символа используется не один знак, а два. Например, при добавлении словоформы «стеной» (СТЕНА в творительном падеже) будет добавлена следующая последовательность пар знаков: «с: С», «т: Т», «е: Е», «н: Н», «о: А», «й:_».

Все словоформы слов «стена» и «стрела» в таком автомате будут выглядеть так:

Такой подход к записи нормальной формы обладает важным достоинством. Он позволяет работать с морфологией в двух направлениях. Можно по словоформе получить ее разбор — анализ. А можно по нормальной форме получить все ее словоформы — синтез.

Недостатком такого подхода является то, что несмотря на то, что для пары знаков автомат является детерминированным, то для входного он уже не является таковым и надо перебирать все переходы из данного состояния. Например состояние m, на рисунке выше. В нем имеется несколько переходов по знаку словоформы «а».

Хранение данных в переходах. Использование аннотаций

Другой способ для хранения дополнительных данных был описан в оригинальной работе. Он предполагает изменение самих строк, которые хранятся в автомате.

Предлагается сделующая схема. Вместо целевой строки в автомат записывается расширенная строка, которая состоит из целевой строки, символа начала данных (аннотирующего символа) и самих данных.

Например, в этом случае морфологические характеристики могут быть записаны следующим образом: «стена|+сущ+жен+им, . », где ‘|’ — аннотирующий символ, а «+cущ», «+жен», «+им» — специальные символы данных.

Этот подход используется в системе АОТ. В ней в качестве данных хранится фактически две ссылки: на морфологические характеристики и на номер правила словоизменения. В результате при анализе можно по словоформе получить как ее морфологические признаки, так и начальную форму.

Особенностью этого подхода является то, что несколько усложняется модель автомата. Символ перехода интерпретируется по-разному в зависимости от того был он до аннотирующего символа или после.

Другой особенностью является то, что для обход по строке несколько усложняется. Во-первых, строка присутствует в автомате, если после ее обхода мы оказываемся в состоянии, из которого есть переход по аннотирующему символу. Во-вторых, необходима процедура сбора всех аннотаций после аннотирующего символа. В третьих, необходима процедура декодирования аннотации.

Оптимизация объема памяти

Для оптимизации объема памяти используется два представления конечных автоматов: один для построения минимального автомата, а другой — для анализа. Разница между ними в том, что автомат для анализа не предполагает изменений и поэтому может быть более эффективно размещен в памяти.

Автомат для анализа состоит из трех структур:

1. таблица переходов — пары целых
2. индексы начала и конца диапазона переходов состояния
3. таблица данных финальных состояний

Автоматы получаются достаточно компактными. Например, словарь АОТ без особых ухищрений занимает около 8Мб. Полные данные системы морфологического анализа, которые включают в себя не только анализ по словарю, но и предиктивный анализ слова умещаются в 16Мб.

Источник