- Асимптоты графика функции
- Вертикальные асимптоты
- Горизонтальные асимптоты
- Наклонные асимптоты
- Примеры решений
- Асимптоты графика функции
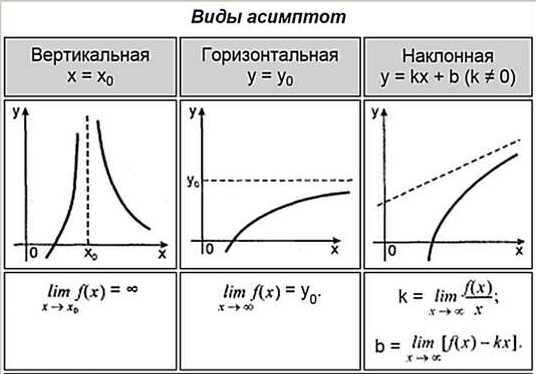
- Виды асимптот
- Нахождение наклонной асимптоты
- Асимптоты
- п.1. Понятие асимптоты
- п.2. Вертикальная асимптота
- п.3. Горизонтальная асимптота
- п.4. Наклонная асимптота
- п.5. Алгоритм исследования асимптотического поведения функции
- п.6. Примеры
Асимптоты графика функции
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три. и бесконечно много. У каждой функции по разному.
Вертикальные асимптоты
Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.
Горизонтальные асимптоты
Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Наклонные асимптоты
Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ — это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ \infty $, тогда наклонной асимптоты нет. А если $ b = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Примеры решений
| Пример 1 |
| Найти все асимптоты графика функции $$ f(x) = \frac<5x> <3x+2>$$ |
| Решение |
| Ответ |
| $$ y = \frac<5> <3>$$ |
| Пример 2 |
| Найти все асимптоты графика функции $ f(x) = \frac<1> <1-x>$ |
| Решение |
| Ответ |
| $$ y=0 $$ |
| Пример 3 |
| Найти все асимптоты графика функции $ f(x) = \frac |
| Решение |
| Ответ |
| $$ y =\frac<1><3>x $$ |
| Пример 4 |
| Найти асимптоты $ f(x) = xe^ <-x>$ |
| Решение |
| Ответ |
| $$ y = 0 $$ |
Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.
Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.
Источник
Асимптоты графика функции
Виды асимптот
Прямая $x=x_<0>$ называется вертикальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _
Замечание. Прямая $x=x_<0>$ не может быть вертикальной асимптотой, если функция непрерывна в точке $x=x_<0>$ . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Прямая $y=y_<0>$ называется горизонтальной асимптотой графика функции $y=f(x)$, если хотя бы одно из предельных значений $\lim _
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая $y=k x+b$ называется наклонной асимптотой графика функции $y=f(x)$, если $\lim _
Нахождение наклонной асимптоты
(условиях существования наклонной асимптоты)
Если для функции $y=f(x)$ существуют пределы $\lim _
Горизонтальная асимптота является частным случаем наклонной при $k=0$ .
Если при нахождении горизонтальной асимптоты получается, что $\lim _
Кривая $y=f(x)$ может пересекать свою асимптоту, причем неоднократно.
Задание. Найти асимптоты графика функции $y(x)=\frac
Решение. Область определения функции:
$D[f] : x \in(-\infty ;-1) \cup(-1 ;+\infty)$
а) вертикальные асимптоты: прямая $x=-1$ — вертикальная асимптота, так как
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты $y=k x+b$:
Таким образом, наклонная асимптота: $y=x-4$ .
Ответ. Вертикальная асимптота — прямая $x=-1$ .
Источник
Асимптоты
п.1. Понятие асимптоты
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
 Вертикальная асимптота x=3 |  Горизонтальная асимптота y=1 |
 Наклонная асимптота y=x | |
п.2. Вертикальная асимптота
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции \(y=\frac<1><(x-1)(x+3)>\)
ОДЗ: \(x\ne \left\<-3;1\right\>\)
\(\left\
Исследуем \(x_0=-3\). Найдем односторонние пределы: \begin
Точка \(x_0=-3\) — точка разрыва 2-го рода.
Исследуем \(x_1=1\). Найдем односторонние пределы: \begin
Точка \(x_1=1\) — точка разрыва 2-го рода.
Вывод: у функции \(y=\frac<1><(x-1)(x+3)>\) две точки разрыва 2-го рода \(\left\
п.3. Горизонтальная асимптота
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции \(y=\frac<1><(x-1)(x+3)>\)
Ищем предел функции на минус бесконечности: \begin
Ищем предел функции на плюс бесконечности: \begin
Вывод: у функции \(y=\frac<1><(x-1)(x+3)>\) одна горизонтальная асимптота \(y=0\). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции \(y=\frac<1><(x-1)(x+3)>\):
п.4. Наклонная асимптота
Число наклонных асимптот не может быть больше двух.
Чтобы построить график асимптотического поведения, заметим, что у функции \(y=\frac
График асимптотического поведения функции \(y=\frac
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция \(y=f(x)\)
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) \( y=\frac<4x>
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: \(x=\pm 1\)
Односторонние пределы в точке \(x=-1\) \begin
Односторонние пределы в точке \(x=1\) \begin
Функция имеет две вертикальные асимптоты \(x=\pm 1\)
График асимптотического поведения функции \(y=\frac<4x>
2) Горизонтальные асимптоты
Пределы функции на бесконечности: \begin
График асимптотического поведения функции \(y=e^<\frac<1>
в) \( y=\frac
Заметим, что \( \frac
3) Наклонные асимптоты
Ищем угловые коэффициенты: \begin
Ищем свободный член: \begin
График асимптотического поведения функции \(y=\frac
2) Горизонтальные асимптоты
Пределы функции на бесконечности: \begin
Функция не имеет горизонтальных асимптот.
График асимптотического поведения функции \(y=xe^<\frac<1><2-x>>\)
Источник