Анализ это способ рассуждения

Алгоритм анализа рассуждений в логике высказываний

Для логического анализа рассуждений (умозаключений) полезно пользоваться алгоритмом анализа, разработанного современной математической логикой, т.е. соответствующей теорией и техникой.

Алгоритм (техника, процедура точного однозначного решения) формально-логического анализа рассуждения включает в себя последовательное осуществление следующих действий (шагов):

1) найти и построить символическую форму рассуждения;

2) определить при помощи теории и техники логики высказываний, следует ли заключение рассуждения из посылки (посылок) рассуждения (см. приложения 1 и 2);

3) доказать заключение, т.е. построить вывод заключения из посылок при помощи правил вывода логики высказываний (см. приложение 3).

1. Определение и построение символической формы рассуждение предполагает:

1) выделение в рассуждении простых, законченных, повествовательных (утвердительных или отрицательных) или сводимых к ним предложений;

2) замещение (обозначение) выделенных простых предложений переменными (А, В, С, …);

3) представление как посылок, так и заключения (вывода) в виде связей между соответствующими предложениями, т.е. конъюнкций, дизъюнкций, импликаций, отрицаний и т.д. этих простых предложений.

Результатом перевода рассуждения в символическую форму будет являться утверждение о логическом следовании заключения некоторого вида из посылок некоторого вида.

В данном примере:

╞ — знак логического следования;

(А → В) – посылка («Неверно, что если подсудимый виновен, то у него был сообщник»);

В) – заключение («Подсудимый виновен, а сообщника у него не было»).

Найденная и построенная символическая форма рассуждения позволяет анализировать при помощи техники логики высказываний отношение логического следования между посылками и заключением.

2. Согласно постулатам связи отношений логического следования и общезначимых формул имликативного вида (см. приложение 2) записываем полученную символическую форму рассуждения в виде импликативной формулы, в которой посылка занимает место аптецедента импликации, а заключение – консеквента импликации.

a) Если символическая форма рассуждения имела вид

то полученная по 1-му постулату импликативная формула будет иметь вид

b) Если же символическая форма рассуждения имела вид

то полученная по 2-му постулату импликативная формула будет иметь вид

Теперь, применяя технику табличного установления общезначимости или технику «сведения к абсурду», определяем, является ли полученная формула общезначимой (тавтологией). Из посылок некоторого вида будет логически следовать заключение, если, и только если, соответствующая символической форме рассуждения формула является общезначимой.

3. Если формула общезначима, а следовательно, заключение рассуждения логически следует из посылок, строим вывод заключения, т.е. показываем, каким именно способом, по каким правилам вывода может быть осуществлен переход от посылок к заключению.

Проведем в качестве примера анализ следующих рассуждений:

a) «Не скажи он ей, она не узнала бы. А не спроси она его, он ни за что не сказал бы ей. Но она узнала. Значит, она его спросила».

b) «Если бы он не получил лицензию, то либеральная доктрина потеряла бы красноречивого сторонника. А не будь Катя молчаливой, он ни за что не получил бы лицензию. Он, однако, продолжает защищать либеральную доктрину. Значит, Катя молчалива».

1. Выделим в рассуждениях простые, повествовательные (или сводимые к ним) предложения и заменим их на переменные.

a) «Он не сказал ей» —

«Она спросила» — С

«Она его не спросила» —

b) «Он не получил лицензию» —

«Либеральная доктрина теряет (не имеет) сторонника» —

«Катя не молчалива» —

«Либеральная доктрина имеет сторонника» — В

«Катя молчалива» — С

Легко заметить, что состав простых предложений в обоих рассуждениях одинаков.

Теперь посмотрим, каким способом в рассуждениях связаны простые предложения, и в соответствии с формой их связи найдем символическую форму рассуждений:

В – первая посылка;

А – вторая посылка;

В – третья посылка;

Таким образом, символическая форма обоих рассуждений имеет вид:

Здесь в скобках зафиксированы 3 посылки, из которых, как это утверждается в рассуждениях, следует заключение С, а ╞ — знак логического следования.

2. Согласно 2-му постулату (см. приложение 2) записываем полученное утверждение о логическом следовании в виде импликации, в которой антецедент – конъюнкция трех посылок, а консеквент – заключение.

Теперь относительно полученной формулы, применяя технику косвенного доказательства общезначимости (метод «сведения к абсурду»), определяем, является ли формула общезначимой.

Для этого мы допускаем, что формула не является общезначимой, а значит, что по крайней мере в одном случае значение истинности основной импликации – «ложно» ( = О )

((

О О

1 основное допущение косвенного

доказательства общезначимости формулы

Но тогда, согласно таблице истинности импликации, С = О, а

поскольку импликация ложна только в одном случае (см. приложение 1).

Переносим значение истинности С ( С = О ) в антецедент основной импликации. Но если С = О, то

((

Если антецедент основной формулы имеет значение «истинно», а он является конъюнкцией трех подформул, то конъюнкция должна быть истинной

((

1 1 О 1 О О

Конъюнкция истинна тогда и только тогда, когда все составляющие конъюнкцию имеют значение истинности «истинно», а значит:

((

1 1 1 О 1 1 1 О О

1

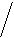
В = 0, а значит, если (

(см. таблицу для импликации, приложение 1).

Распределение значений истинности будет иметь вид

((

О 1 1 О 1 1 1О 1 О1 1 1 О О

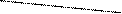
А = 0, то формула (

А = 0. Однако эта же формула (

А) = 1 согласно основному допущению.

0 1 1 0 1 1 1 0 1 0 1 1 1 0

Таким образом, допущение: «Формула не является общезначимой» приводит нас к противоречию. Действительно, одна и та же формула (

А) для того, чтобы реализовать допущение, должна быть одновременно и истинной, и ложной. Противоречивое допущение должно быть отброшено, а значит, основная формула является общезначимой. Но тогда рассуждения, имеющие символическую форму

являются логически правильными – в них заключение логически следует из посылок.

3. Построение вывода заключения из посылок.

Выводом заключения из посылок будем называть конечную последовательность высказываний (формул), каждое из которых либо посылки (гипотеза), либо логически следует из посылок по одному из правил вывода.

В нашем примере:

1.

3. В — посылка (3)

В (высказывание следует из (1) и (2) по правилу

5. С (высказывание следует из (4) и (3) по правилу

Вариантом вывода может быть:

4¢. А (высказывание следует из (1) и (3) по правилу

5¢. С (высказывание следует из (2) и (4¢) по правилу modus

Источник

АНАЛИЗ

Философский энциклопедический словарь. — М.: Советская энциклопедия . Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов . 1983 .

Философский энциклопедический словарь . 2010 .

Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия . Под редакцией Ф. В. Константинова . 1960—1970 .

Новая философская энциклопедия: В 4 тт. М.: Мысль . Под редакцией В. С. Стёпина . 2001 .

Полезное

Смотреть что такое «АНАЛИЗ» в других словарях:

анализ — подтвердил • субъект, оценка, регистрация анализ позволил • возможность, субъект, модальность анализ показал • субъект, демонстрация анализ показывает • субъект, демонстрация анализ проводится • действие, пассив на ся анализ проводить • действие… … Глагольной сочетаемости непредметных имён

Анализ — (др. греч. ἀνάλυσις разложение, расчленение) операция мысленного или реального расчленения целого (вещи, свойства, процесса или отношения между предметами) на составные части, выполняемая в процессе познания или предметно практической … Википедия

анализ — – исследование, а также его метод и процесс, имеющие целью установление одной или нескольких характеристик (состава, состояния, структуры) вещества в целом или отдельных его ингредиентов. Словарь по аналитической химии [3] • атомно абсорбционный… … Химические термины

АНАЛИЗ — (от греч. analyein разбирать). 1) разбор, разложение па составные части, элементы, расчленение. 2) способность ума разделять познаваемое понятие на составные части по его признакам. 3) анализ математический Учение о переменных величинах. Словарь… … Словарь иностранных слов русского языка

анализ — а м. analyse f. нем. Analysis < , ср. лат. analysis. 1. Способ научного рассмотрения предметов или явлений путем разложения их на первичные, простейшие элементы, основания. Сл. 18. Сделать Анализ и речи. Ян. 1 136. Без анализа мы вечно бродили … Исторический словарь галлицизмов русского языка

анализ — Разложение, разбор, расследование. Ср … Словарь синонимов

анализ — 1) Метод научного исследования, состоящий в мысленном или фактическом разложении целого на составные части. 2) Химический анализ совокупность операций, имеющих целью установить, из каких веществ состоит исследуемый объект (качественный анализ)… … Справочник технического переводчика

АНАЛИЗ — (от греч. analysis разложение) метод научного исследования (познания) явлений и процессов, в основе которого лежит изучение составных частей, элементов изучаемой системы. В экономике анализ применяется с целью выявления сущности, закономерностей … Экономический словарь

АНАЛИЗ — • АНАЛИЗ, в математике область применения таких понятий, как сходимость, НЕПРЕРЫВНОСТЬ, ИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ. Математический анализ заключается в приложении этих понятий к действительным числам и функциям действительных чисел.… … Научно-технический энциклопедический словарь

АНАЛИЗ — АНАЛИЗ, анализа, муж. (греч. analysis). 1. Метод исследования, состоящий в расчленении исследуемого предмета или явления; ант. синтез (филос.). Подвергнуть анализу понятие причинности. 2. Разложение какого нибудь вещества на составные его… … Толковый словарь Ушакова

Источник

4.7. Логический анализ рассуждений в естественном языке

4.7. Логический анализ рассуждений в естественном языке

Исчисление предикатов дает возможность проводить логический анализ несравненно большего количества рассуждений, выраженных на естественном языке, чем исчисление высказываний. В самом деле, с помощью нового исчисления становится возможным представить символически количественные характеристики суждений. Именно для этого вводятся кванторы общности и существования, выражающие универсальные (общие) суждения и частные суждения. Но самое главное преимущество исчисления предикатов перед исчислением высказываний состоит в том, что оно дает возможность символически представить внутреннюю логическую структуру суждения. Такая структура выражается либо с помощью субъектно-предикатного отношения предмета (субъекта) и его свойства или признака (предиката), либо n-местного отношения между различными предметами.

Повседневные и многие научные рассуждения обычно ведутся на естественном языке. Но, как уже неоднократно упоминалось, такой язык развивался в интересах легкости общения, обмена мыслями в ущерб точности и ясности. Логические исчисления строятся для того, чтобы обеспечить необходимую точность нашим рассуждениям, вскрывать возникающие при этом ошибки и исправлять их. В простейших случаях такой анализ можно провести с помощью исчисления высказываний, в котором мы отвлекаемся от логической структуры суждений и рассматриваем их как нечто единое целое, как далее неразложимые атомы рассуждения. Но средств этого исчисления оказывается явно недостаточно, когда приходится анализировать многие наиболее распространенные рассуждения не только в науке, но и в повседневном мышлении. Силлогистика Аристотеля, как мы видели, охватывает неизмеримо больший класс рассуждений, но она оставляет вне рассмотрения рассуждения, в которых фигурируют различные типы отношений. Точный анализ именно таких отношений играет существенную роль в научном познании, в особенности в математике и ее приложениях, в точном естествознании. Поэтому возникновение логики отношений значительно раздвинуло границы применимости логического анализа. С другой стороны, применение символического языка и точных математических методов в новой символической логике, обогащенной логикой отношений, в огромной степени повысило эффективность, строгость и точность такого анализа.

Перевод рассуждений с естественного языка на язык исчисления высказываний, как мы видели в предыдущей главе, наталкивается на серьезные трудности потому, что сильно искажает реальный процесс рассуждений, в котором интересуются не только различными связями суждений друг с другом, но и структурой самих суждений. Исчисление предикатов дает возможность более адекватно отобразить рассуждения, ведущиеся на естественном языке.

Для исчисления предикатов прежде всего устанавливается универсум рассуждения или предметная область объектов, о которых идет речь. Заранее устанавливать, из каких именно объектов состоит универсум рассуждения, не требуется. Достаточно допустить, что такой универсум существует. Далее следует выбрать предикаты (или пропозициональные функции), с помощью которых формулируются логические отношения между переменными. Каждый из выбранных предикатов становится высказыванием, когда все его переменные принимают какое-либо значение из универсума рассуждений, т.е. когда переменные становятся объектами (элементами) универсума рассуждения. Полученное высказывание будет либо истинным, либо ложным, но не тем и другим одновременно. Затем выбирается соответствующая символика для окончательного перевода естественного рассуждения на язык исчисления предикатов. Разумеется, при этом приходится делать определенные упрощения, ибо логика ставит своей целью исследование связи мыслей в рассуждении, выводов из одних суждений к другим.

Преимущество исчисления предикатов перед силлогистикой Аристотеля состоит не только в более широком анализе различных видов умозаключений, но и в точности и ясности получаемых заключений. В этом можно убедиться, если представить в символической записи категорические суждения, которые рассматриваются в силлогистике Аристотеля. Общеутвердительное суждение в исчислении предикатов записывается в виде: (х) (S(x) ? Р(х)), где S и Р обозначают соответственно субъект и предикат. Общеотрицательное суждение можно представить как ¬ (Ex) (S(x) ? Р(х)), частноутвердительное — как (Ex) (S(x) ? Р(х)), частноотрицательное — как (Ех) (S (х) ? ¬ Р(х)).

При переводе с естественного языка на символический как раз и обнаруживается двусмысленность употребления общих суждений, подобная той, которая связана с использованием в разговорном языке союза «или». В предыдущей главе, говоря о союзе «или», мы различали его употребление во включающем и исключающем смысле, т.е. объединительную и разделительную дизъюнкцию. Аналогично этому при логическом анализе общих суждений атрибутивного характера нет необходимости предполагать заранее универсум

рассуждения пустым множеством, хотя и в повседневных рассуждениях. В аристотелевской силлогистике также считают, что такой универсум является непустым множеством. Однако в современной логике допускают, что в суждении «Все S есть F» множество может оказаться и пустым, а само суждение следует тогда считать истинным. Подобных трудностей не возникает с употреблением частных суждений, где существование по крайней мере одного объекта множества постулируется квантором существования.

Современный подход к интерпретации общих категорических суждений более предпочтителен хотя бы потому, что заранее не всегда известно, пуста или не пуста область значений субъекта с определенными предикатами, т.е. существуют ли предметы с данными свойствами. Для того чтобы представить аристотелевскую интерпретацию силлогистики, достаточно дополнить символическое представление общего категорического суждения квантором существования.

Проверьте себя

1. Почему предикат можно рассматривать как пропозициональную функцию? Пусть предикат выражает отношение «больше» по величине между числами: х > у.

1) При каких значениях х и у он образует истинные и ложные высказывания?

2) Тот же вопрос, если х = у.

2. Что называют универсумом рассуждения?

1) Определите универсум рассуждений формул х 2 + 1 = 0 и х 2 — 1 = 0.

2) Каков универсум определения «Все четные числа делятся на 2»?

3) Определите универсум рассуждения «Все студенты нашей группы получают стипендию».

3. Чем отличаются свойства от отношений и как они выражаются символически?

Переведите на символический язык следующие утверждения:

1) «Москва — столица России и находится южнее Санкт-Петербурга».

2) «Золото — металл и ценится дороже серебра».

3) «Если человек заболел гриппом, то у него повышается температура».

4. Какие переменные называются свободными и связанными? Определите область действия кванторов в следующих формулах:

1) (х) (А(х) ? В(х)) ? С(х); (Ех) (А(х) ? B(x));

2) (х) (Еу) (х 1, А 2. A m, в исчислении предикатов?

8. Какие проблемы в логике считаются разрешимыми и неразрешимыми?

Разрешима ли проблема определения тавтологии в исчислении высказываний? Проверьте это для формулы: А ? В

9. Правильно ли построены следующие силлогизмы?

1) Все рыбы дышат «жабрами». Кашалот не дышит жабрами. Следовательно, кашалот — не рыба».

2) «Мысль — это движение. Движение есть свойство всей материи. Значит, мысль есть свойство всей материи».

3) «Логика изучает формы и законы правильного мышления. Учение о понятии есть часть логики. Следовательно, оно изучает законы и формы правильного мышления».

4) «Всякий предмет состоит из молекул. Логика не состоит из молекул. Следовательно, логика не является предметом».

5) «Истинное суждение правильно отражает действительность. Данная мысль правильно отражает действительность. Следовательно, она является истинным суждением».

10. Превратите следующие силлогизмы в энтимемы.

1) «Липа поглощает углекислоту, так как липа — растение, а все растения поглощают углекислоту».

2) «Ни одна планета не светит собственным светом, но многие тела в Солнечной системе — не планеты, поэтому некоторые тела Солнечной системы светят собственным светом».

3) «Все учителя — педагоги, он учитель, следовательно, он педагог».

11. Являются ли следующие суждения энтимемами:

1) «Поскольку он юрист, он должен знать права человека».

2) «Раз вы не знаете правил логики, то не можете понять ошибки в рассуждении».

3) «Вода замерзла, так как температура понизилась».

12. Найдите ошибку в рассуждении:

1) «Предполагая 2 х 2 = 8 и отнимая от обеих частей по 6, получим -2 = 2. Возведя обе части в квадрат, найдем, что 4 = 4. Значит, 2 х 2 = 8».

13. Определите, правильно ли сделаны следующие выводы:

1) «Если курение вредно, то следует бросить курить. Но некоторые курят без вреда здоровью. Следовательно, не стоит бросать курить».

2) «Если два числа равны друг другу, то их квадраты также равны. Квадраты этих чисел равны. Следовательно, заданные числа также равны».

3) «Иванов может учиться на психологическом, юридическом или экономическом факультете. Он не учится ни на психологическом, ни на юридическом факультете, следовательно, он учится на экономическом факультете».

14. Проверьте правильность рассуждения:

«Вода, например, не горит. А хотите знать почему? Да потому же, почему не горит зола. Вода сама получилась от горения» (М. Ильин).

15. Покажите нелогичность поведения Ходжи Насреддина:

«Однажды Ходжа надел черные одежды и вышел на улицу. Какие-то невежи спросили его: «Ходжа, что с тобой, ты весь в черном?» А Ходжа отвечал: «Умер отец моего сына, и я ношу по нем траур» (Анекдоты о Ходже Насреддине).

Читайте также

3.7. Логический анализ рассуждений естественного языка

3.7. Логический анализ рассуждений естественного языка Рассуждения проводятся на естественном языке, но когда возникают трудности и неясности, тогда приходится обращаться к их логическому анализу. Такой анализ предполагает перевод с естественного языка на язык логики, в

5.2. Основные формы индуктивных рассуждений

5.2. Основные формы индуктивных рассуждений Когда мы определяем индуктивное рассуждение по характеру его заключения, то относим его к более широкому классу вероятностных (или правдоподобных) рассуждений. Но это определение нуждается в указании специфического, видового

2.12. Формализация рассуждений

2.12. Формализация рассуждений Как мы помним, логика анализирует правильное мышление с точки зрения его формы, а не содержания. Поэтому одной из основных логических процедур является установление формы того или иного содержательного высказывания или рассуждения.

3. Логический анализ (Б. Рассел)

3. Логический анализ (Б. Рассел) Бертран Рассел (1872–1970) — всемирно известный английский ученый, философ, общественный деятель. В шестнадцать лет он прочитал «Автобиографию» своего крестного отца Дж. С. Милля, произведшую на него большое впечатление. Перу Милля

Т.Н.Панченко. Стросон и Витгенштейн. Анализ как выявление формальной структуры неформального языка и анализ как терапия

Т.Н.Панченко. Стросон и Витгенштейн. Анализ как выявление формальной структуры неформального языка и анализ как терапия *** Людвиг Витгенштейн и Питер Стросон некоторым образом определяют границы философии анализа, ее начало и конец. Один из них принадлежит к

II. ЛОГИЧЕСКИЙ АНАЛИЗ ЯЗЫКА

II. ЛОГИЧЕСКИЙ АНАЛИЗ ЯЗЫКА Для теоретического построения математики была разработана новая логика. В Венском кружке она вообще стала средством создания теории науки. В отличие от чистой логики прикладная логика была использована для уточнения философских

О естественном и позитивном праве

О естественном и позитивном праве В том, что касается праведности, важно не сходить с пути не только естественного, но и позитивного права. Ибо говорят, что одно право естественное, а другое — позитивное. Естественное право — это то, что нужно совершить через поступок, это

СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ

СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ Вот два примера дедуктивных выводов из рассказа русского юмориста начала века В. Билибина. «Если бы на свете не существовало солнца, то пришлось бы постоянно жечь свечи и керосин. Если бы пришлось постоянно жечь свечи и керосин, то чиновникам

§ 17. Завершение логических рассуждений

§ 17. Завершение логических рассуждений Все наше рассуждение было чисто логическим, оно не осуществлялось в какой-либо «материальной» сфере, или, как мы говорим, и это равнозначно, оно не осуществлялось ни в каком определенном регионе, тут речь шла вообще о регионах и

§ 51. Значение предварительных трансцендентных рассуждений

§ 51. Значение предварительных трансцендентных рассуждений Каждый может, правда, осуществлять рефлексию, и каждый в своем сознании может схватывать рефлексию своим постигающим взором; однако, не этим совершается феноменологическая рефлексия, и схваченное сознание —

§ 34. Принципиальное развитие феноменологического метода. Трансцендентальный анализ как анализ эйдетический

§ 34. Принципиальное развитие феноменологического метода. Трансцендентальный анализ как анализ эйдетический В учении о Я, как полюсе своих актов и субстрате хабитуальностей, мы уже затронули, и притом в важном пункте, проблематику феноменологического генезиса и, таким

1. Главнейшие из предыдущих рассуждений

1. Главнейшие из предыдущих рассуждений Этих рассуждений было у нас достаточно много. Укажем главнейшие. Мы рассуждали о судьбе у Гераклита (ИАЭ I 349 – 350), Эмпедокла (415 – 417), Демокрита (454 – 456, 494) с общими выводами для всей ранней классики (536 – 541). Из средней классики к

ГЛАВА XIII. О ЕСТЕСТВЕННОМ СОСТОЯНИИ ЧЕЛОВЕЧЕСКОГО РОДА В ЕГО ОТНОШЕНИИ К СЧАСТЬЮ И БЕДСТВИЯМ ЛЮДЕЙ

ГЛАВА XIII. О ЕСТЕСТВЕННОМ СОСТОЯНИИ ЧЕЛОВЕЧЕСКОГО РОДА В ЕГО ОТНОШЕНИИ К СЧАСТЬЮ И БЕДСТВИЯМ ЛЮДЕЙ Люди равны от природы. Природа создала людей равными в отношении физических и умственных способностей, ибо хотя мы наблюдаем иногда, что один человек физически сильнее или

В ЕСТЕСТВЕННОМ РИТМЕ

В ЕСТЕСТВЕННОМ РИТМЕ Некоторые считают трудные времена Божественным провидением, Божьей карой. Мне кажется, что Бог никогда не наказывает нас — Он лишь дает нам возможность учиться и развиваться. Мудрые учатся на своих ошибках; глупцы повторяют ошибки вновь и

Заключение живых рассуждений

Заключение живых рассуждений Живое рассуждение совсем не похоже на рассуждение логики. И я начинаю понимать, почему логики, чем дальше, тем меньше говорят о том, что логика — наука о рассуждении. Она действительно ушла от рассуждения к чему-то иному, скажем, к произведению

Схема дальнейших рассуждений

Схема дальнейших рассуждений Есть ли у нас основания считать, что Вселенная не является вечной и беспричинной, что существует и что-то кроме неё? По-моему, такие основания есть.Выстроим цепочку логических альтернатив (взаимоисключающих вариантов). Эта цепочка, состоящая

Источник