Модуль 2. Дифференциальное исчисление функции нескольких переменных
Тема 1. Функции двух переменных, частные производные,
Определение функций двух переменных.
Способы задания функций двух переменных.
Частные производные высших порядков.
*Дифференциал функции двух переменных и его применение.
*Дифференциал второго порядка
Тема 2. Экстремум функции двух переменных
Условный экстремум функции двух переменных
Тема 3. Наибольшее и наименьшее значения функции двух
Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой ограниченной области
* Нахождение наибольшего (наименьшего) значений линейной функции в области, заданной линейными ограничениями
Тема 1. Функции двух переменных.
частные производные, дифференциалы, градиент
Определение функций двух переменных.
Способы задания функций двух переменных.
Частные производные высших порядков.
Дифференциал функции двух переменных и его применение.
Дифференциал второго порядка
Определение функций двух переменных
Функцией двух переменных 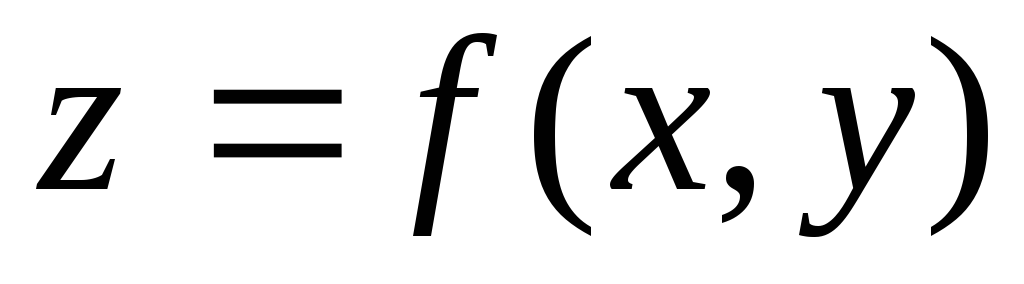
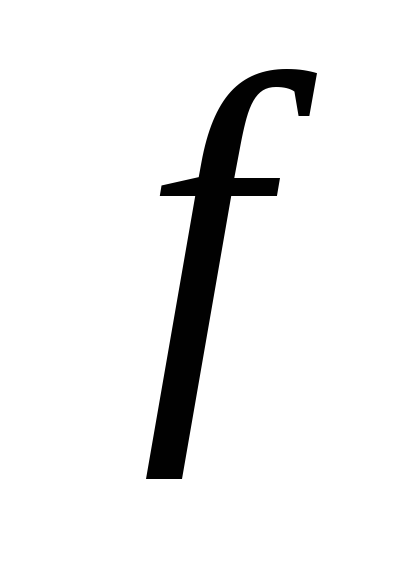
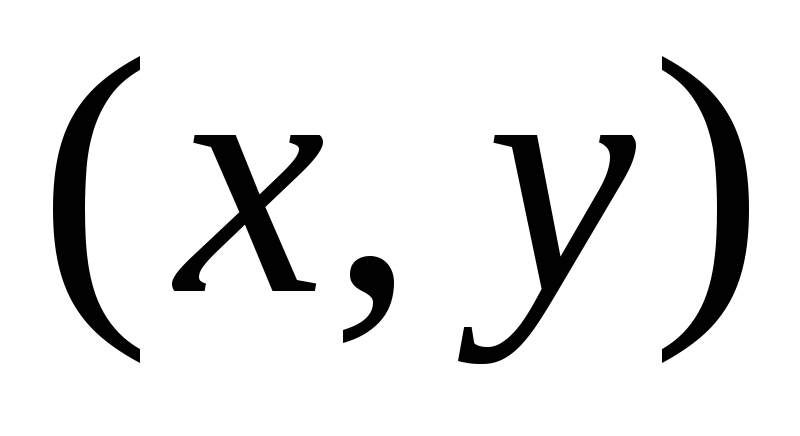
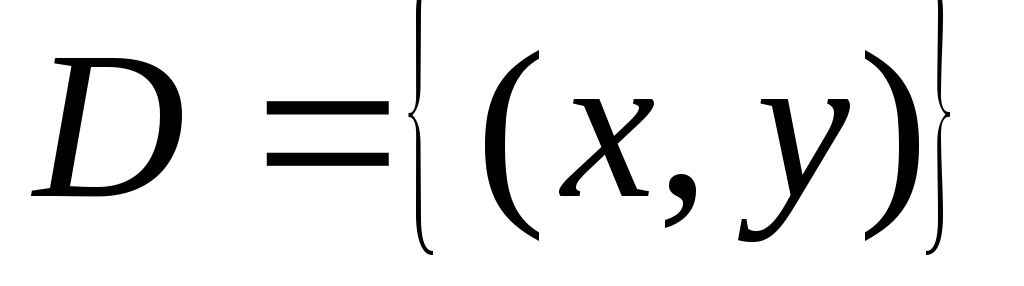


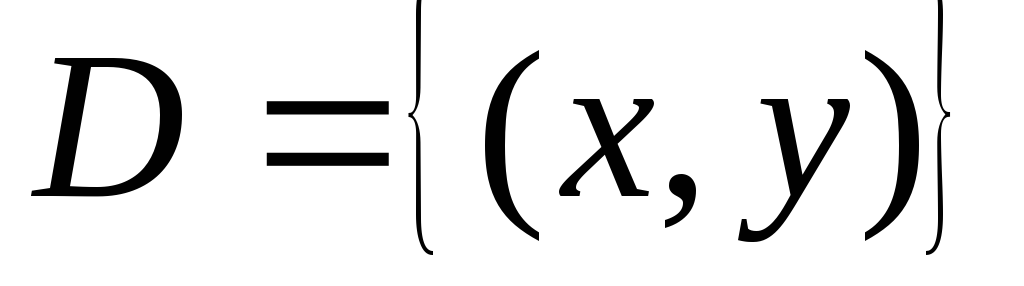
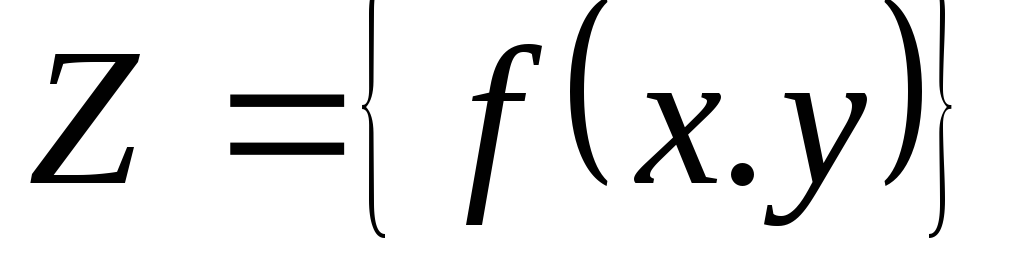
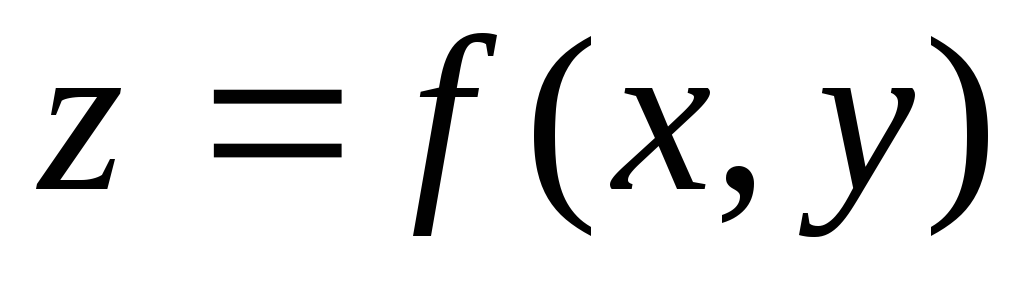
Для функции двух переменных 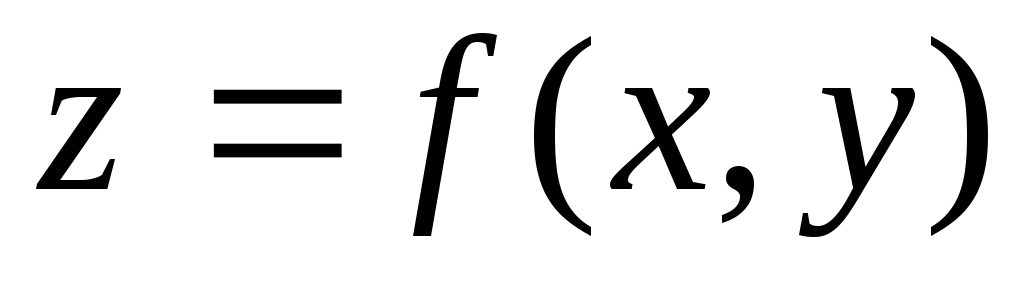

Пример 1. Найти область определения функции 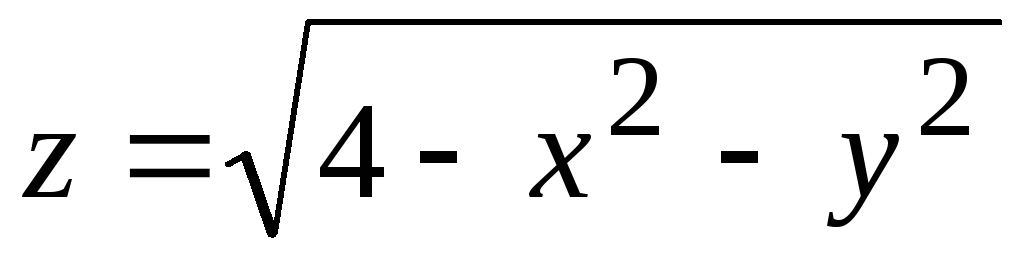
Запишем неравенство 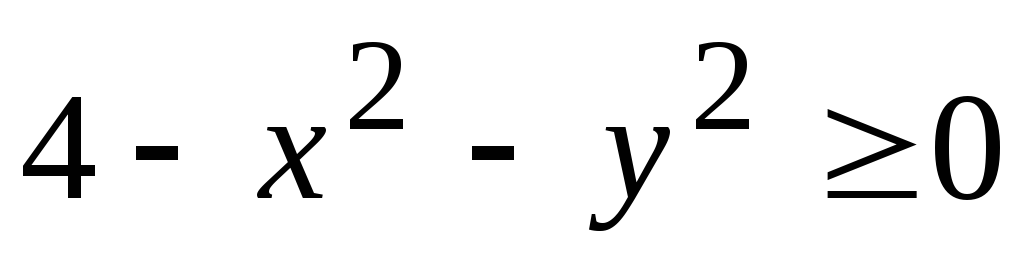
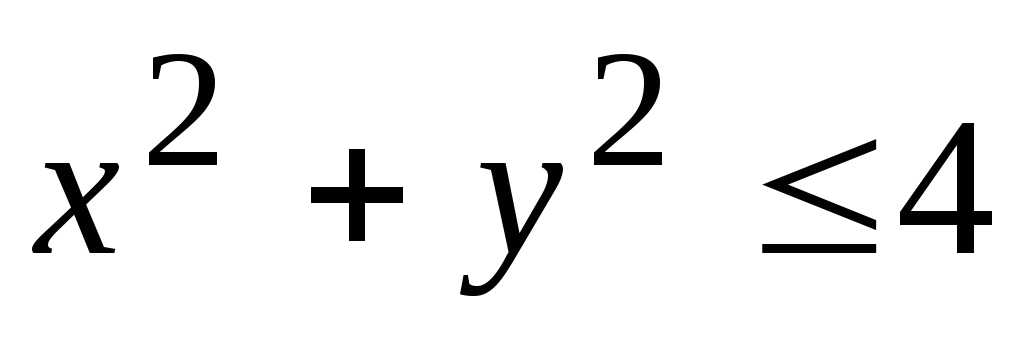
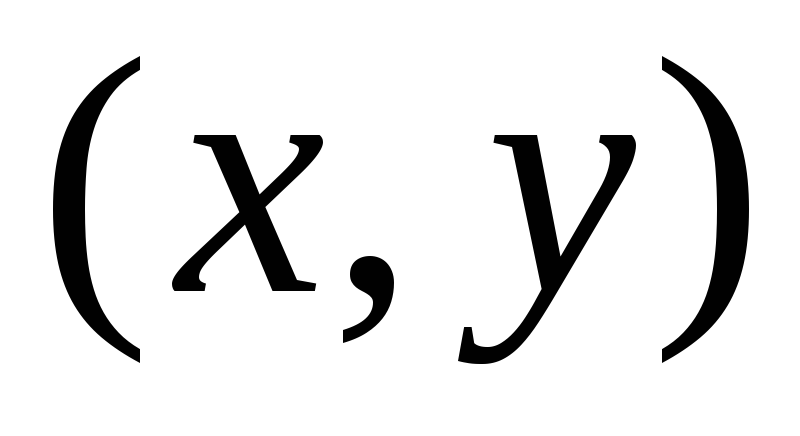
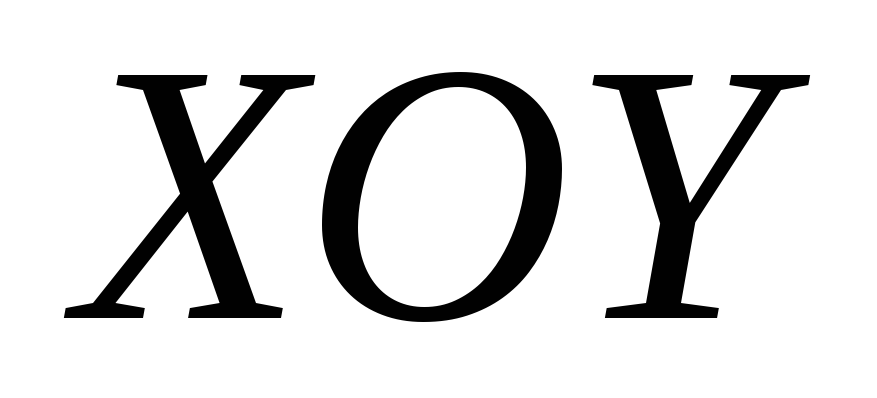
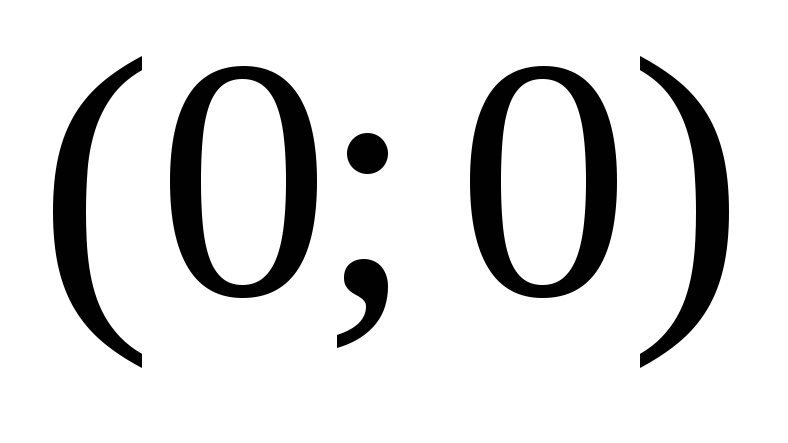

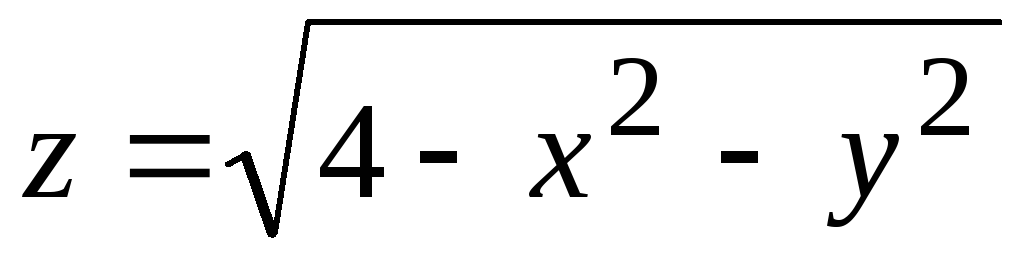

В прямоугольной системе координат 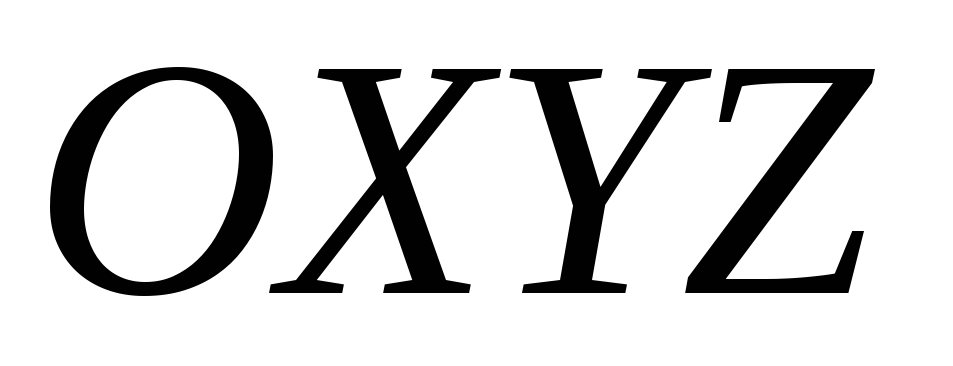
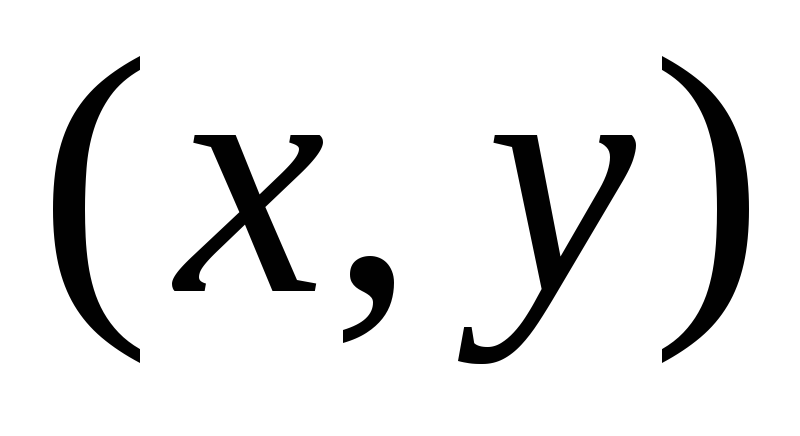
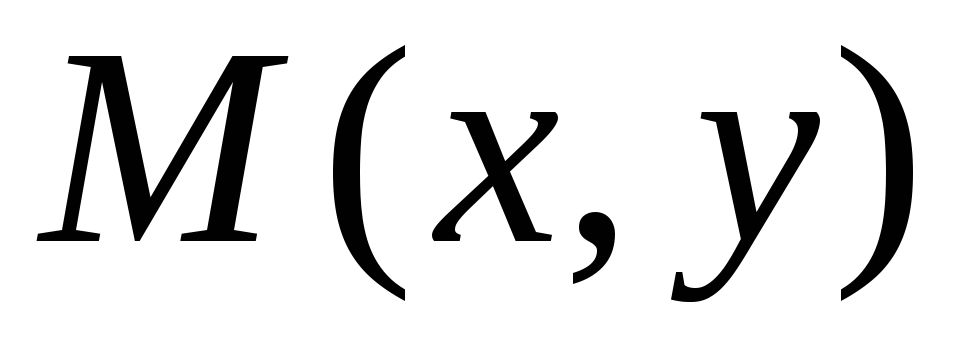

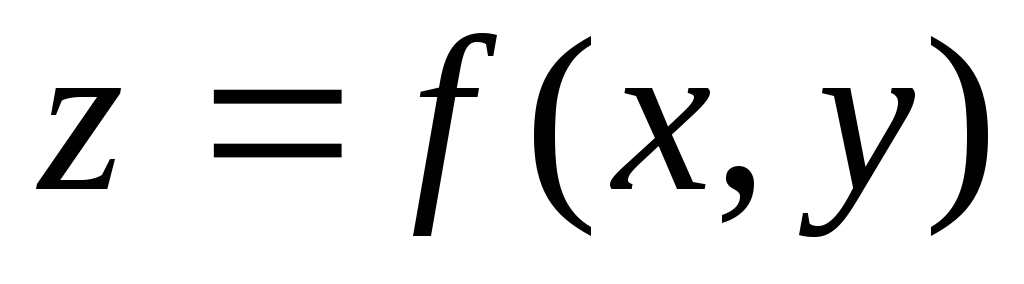
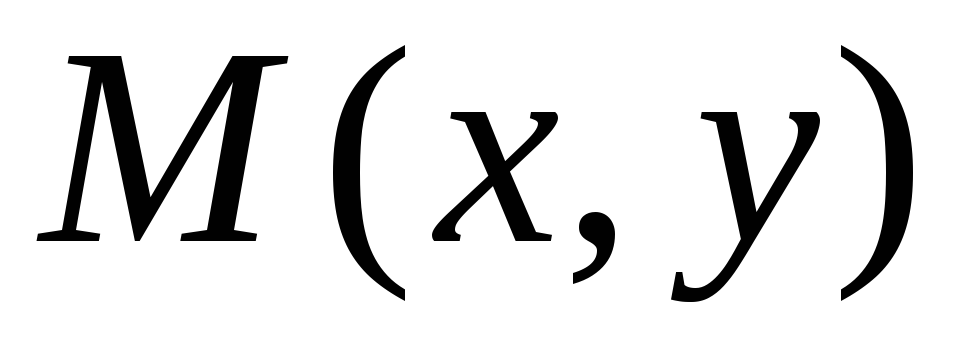

2. Способы задания функций двух переменных
Основными способами задания функций являются аналитический, табличный, графический.
Существует и другие способы задания функций — алгоритмический, с помощью программы на ЭВМ.
Аналитический способ задания функции.
одной формулой, разрешенной относительно зависимой переменной (например, 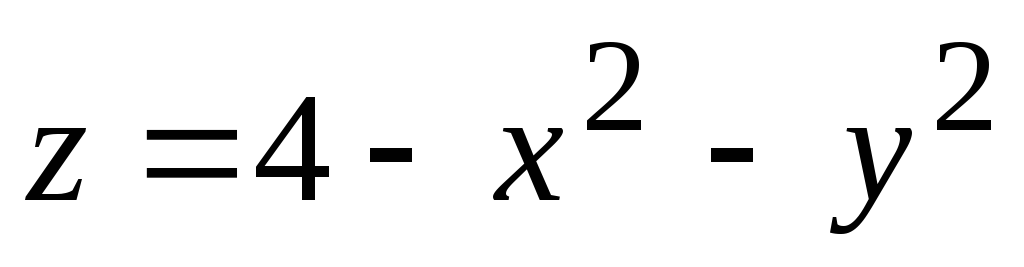
разными формулами на определенных числовых промежутках
Функция двух переменных называется неявной, если она задана уравнением, не разрешенной относительно зависимой переменной. Например, 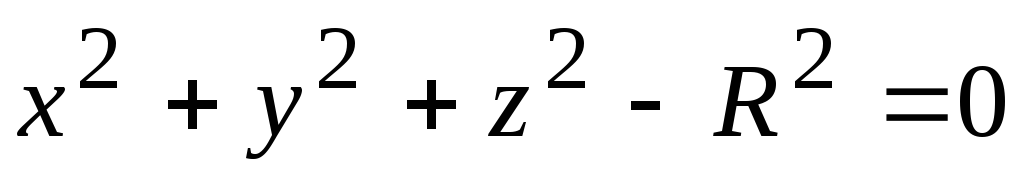
Табличный способ задания функции — с помощью таблицы, в которой указаны значения аргументов и соответствующие им значения зависимой переменной.
Таблица функции двух переменных
Графический способ задания функции.
Графиком функции двух переменных 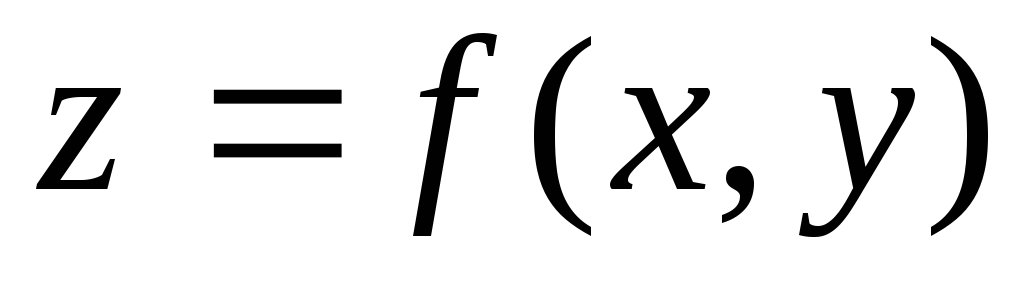
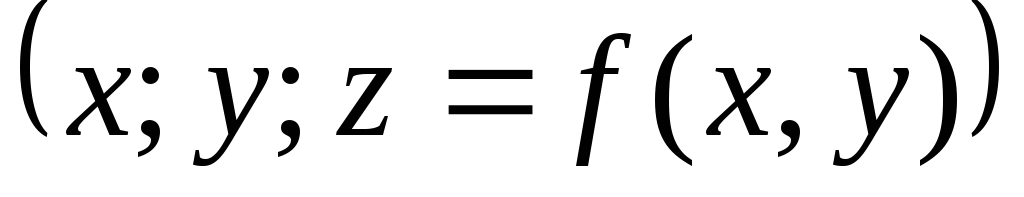

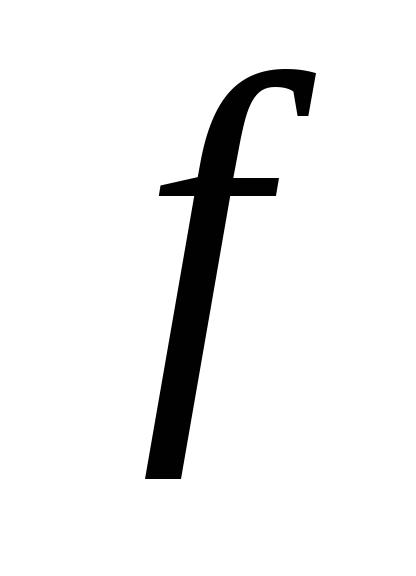
Графиком линейной функции 
Пример 2. Построить график функции 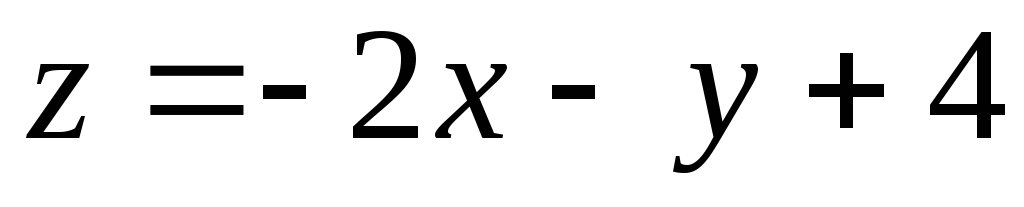
Для функции 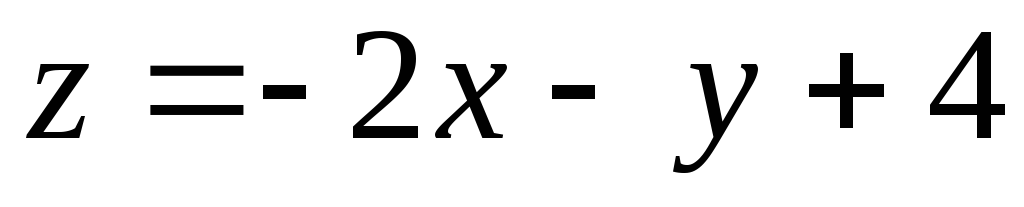
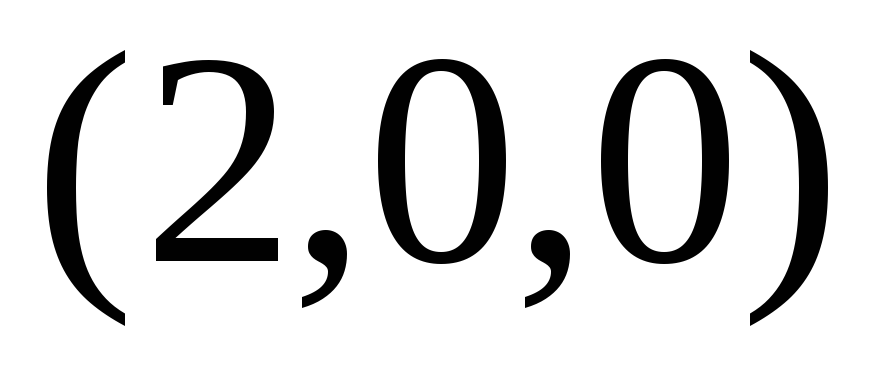
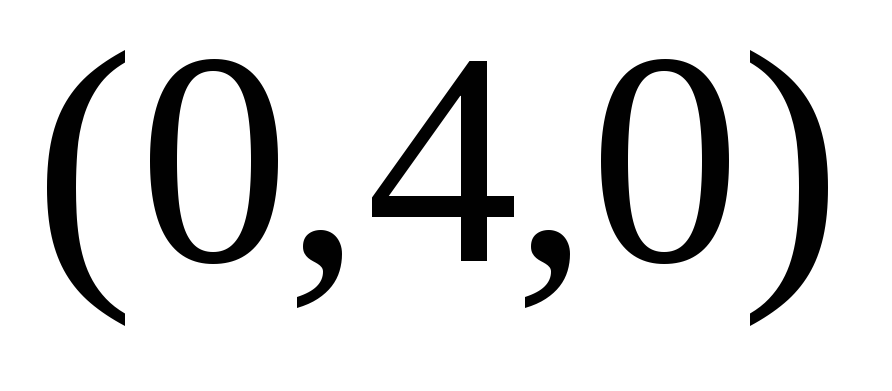
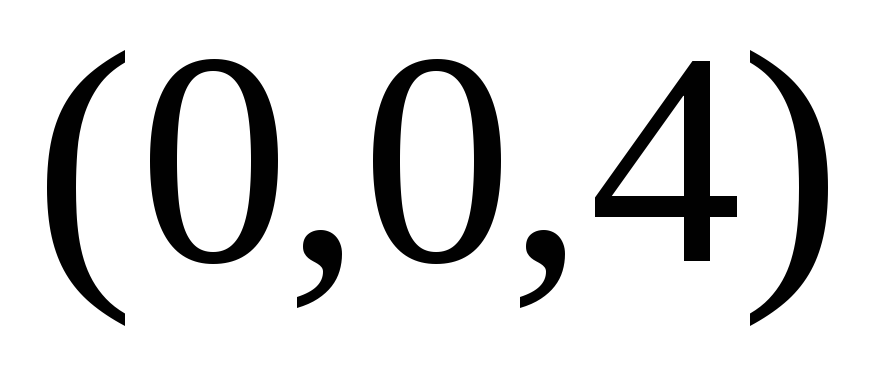

Одним из способов представления функции двух переменных являются линии уровня.
Линией уровня функции 
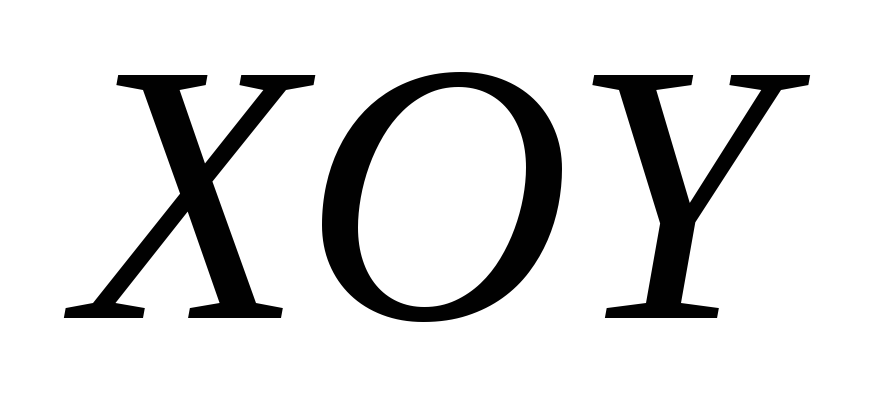
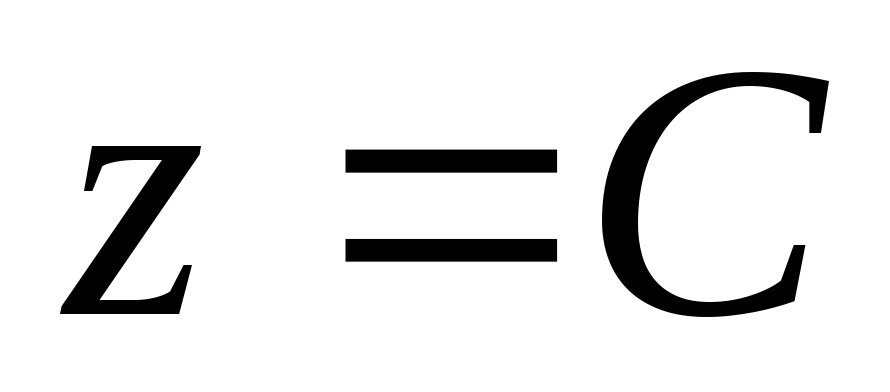

Для линейной функции двух переменных 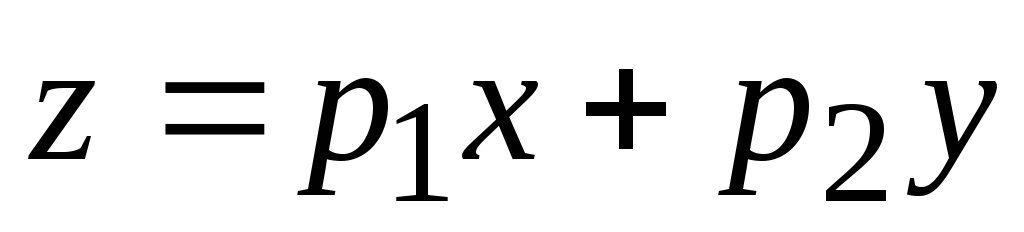
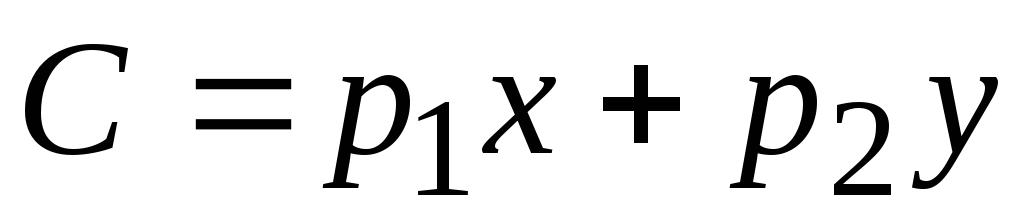
Пример 3. Линиями уровня 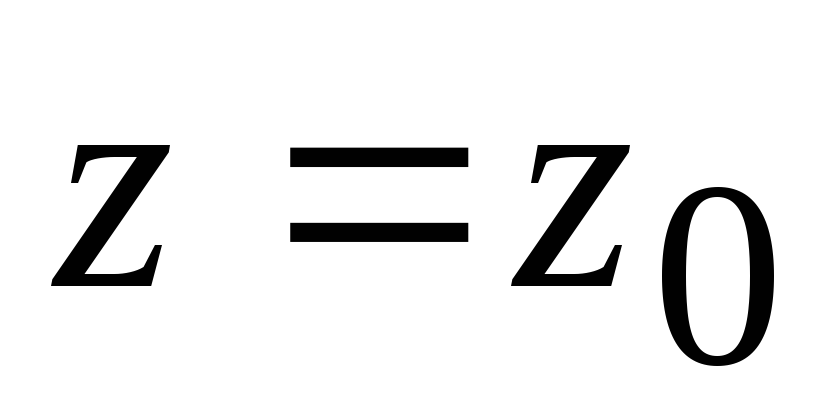
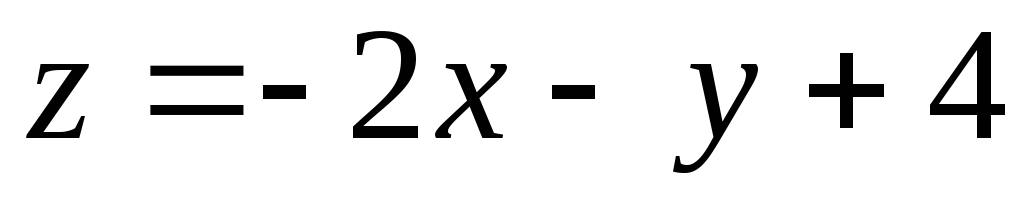
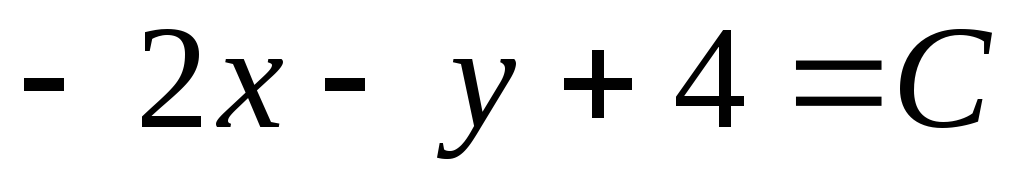
Источник
Функции многих переменных
Способы задания функции многих переменных
Как и функции одной переменной, функции многих переменных можно задавать аналитически, при помощи таблиц, при помощи графика, при помет щи некоторого алгоритма (например, компьютерной программы — см. далее пример 6).
- При аналитическом способе задания функции ее значение определяется формулой от аргументов функции. Функции из примера 1 и из подп. «а», «б» примера 2 были заданы именно так» а функции из подп. «в», «г» примера 2 при желании тоже могли бы быть заданы формулой от соответствующих показателей.
Табличный способ для задания функций многих переменных применяется весьма часто. Например, он иногда необходим в сложных расчетах на ЭВМ. Однако многие, наверное, и не подозревают, что прейскурант обувной или автомастерской частенько табличный способ задания стоимости ремонта в зависимости от выполненных работ. Перечень этих работ — это область определении» а стоимость — значение функции.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример с решением 1:
В мастерской «Шиномонтаж» висит таблица стоимости работ;





Например, клиент привез 5 новых покрышек и хочет сменить все старые покрышки, камеры при этом хочет оставить старые. Тогда
и суммарная стоимость работ равна (6000 4- 8000 + 12 000) х 5 = 130 000 руб.
Конечно, никакой «науки» в этом примере нет, и работник мастерской прекрасно справляется с получением денег от клиентов и без знания, что его прейскурант есть табличный способ задания стоимости ремонта в зависимости от выполненных работ. Графический способ задания функции более чем двух переменных почти не применяется из-за трудностей изображения графика такой функции, В случае же функции 


Возможно вам будут полезны данные страницы:
Пример с решением 2:
Например, для функции 
полусфера над началом координат Радиусом 4 (рис. 1).
Для образного представления функции многих переменных используются линии заданного уровня.
Пусть 





Пример с решением 3:
Пусть 

. Легко видеть, что линии уровня — это «веточки» гиперболы в 1-ми 3-м квадрантах. При увеличении с линии уровня отодвигаются от начала координат (рис. 2).
Компьютерный способ задания функции проиллюстрируем таким примером.
Пример с решением 4:
Рассмотрим линейную задачу оптимального планирования: найти такой план производства X который бы был допустимым и обеспечивал наибольшую прибыль из всех Рис. 2 допустимых планов;
Напомним, что здесь Ф — матрица норм расхода, С — вектор-строка удельных прибылей, В — вектор — столбец запасов ресурсов, Х — вектор-столбец объемов выпускаемой продукции (об этой задаче см. п. 1 раздела 3.1).
Решением этой задачи является оптимальный план Х* и максимальная прибыль 


Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник



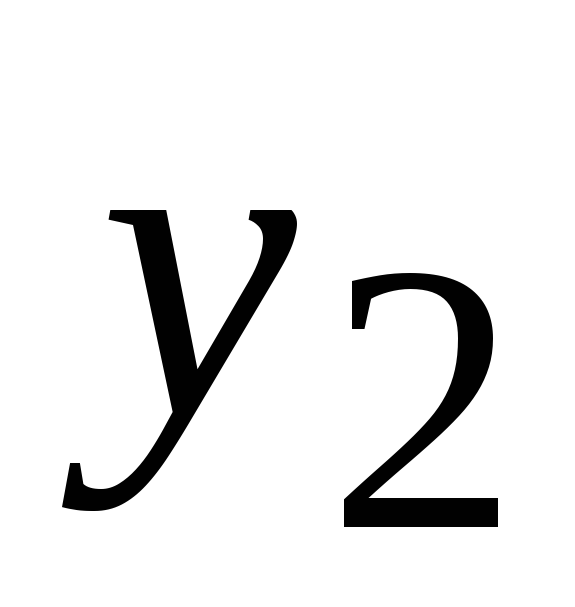
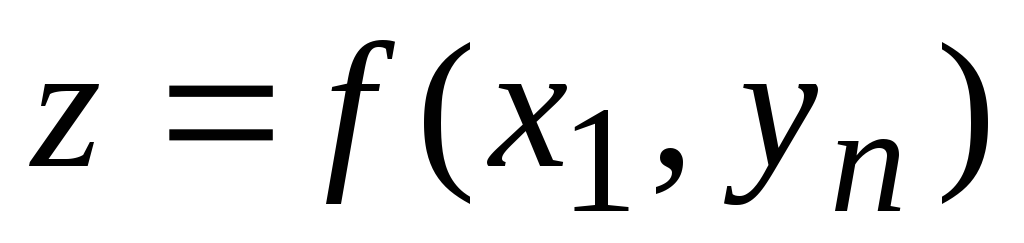
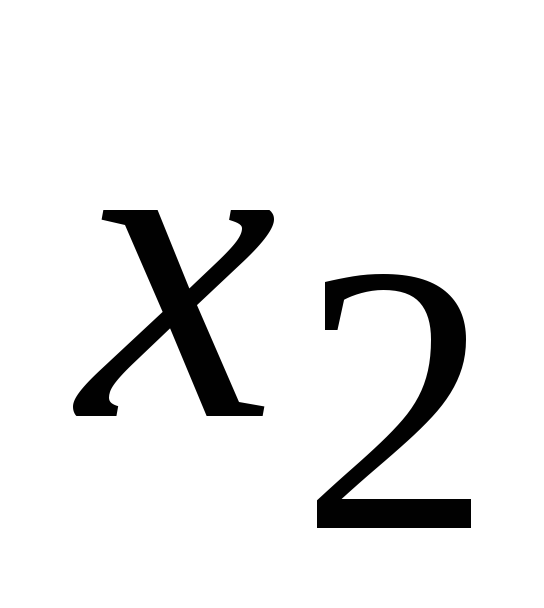
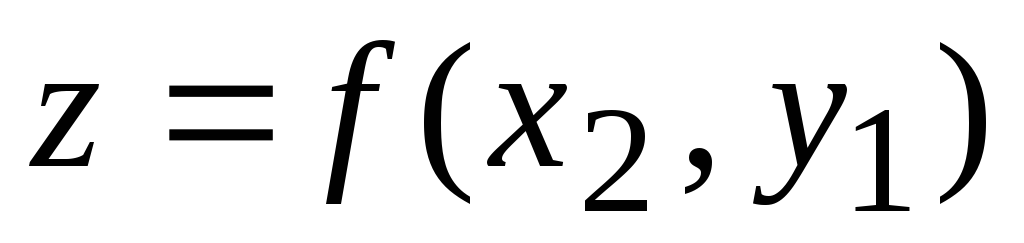

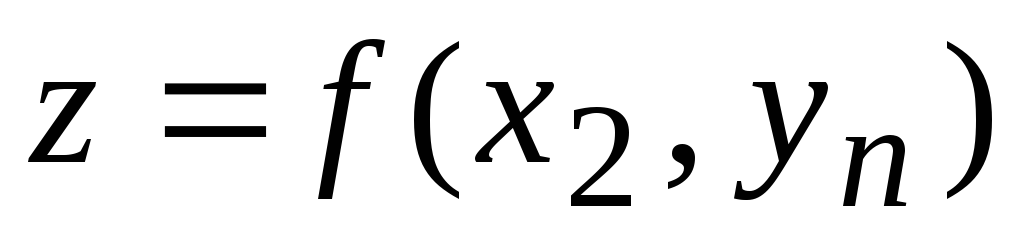

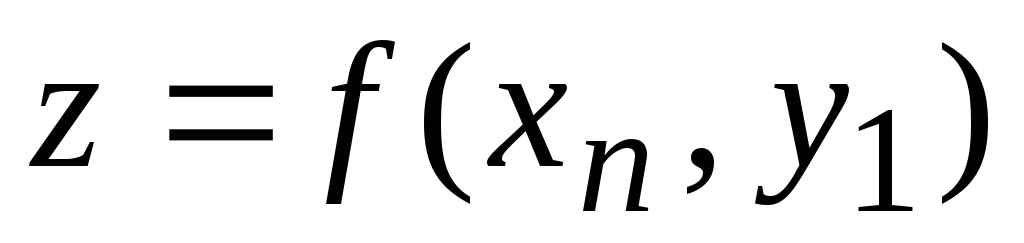
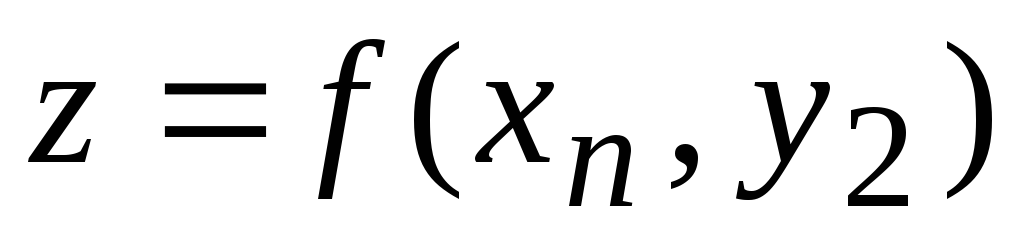
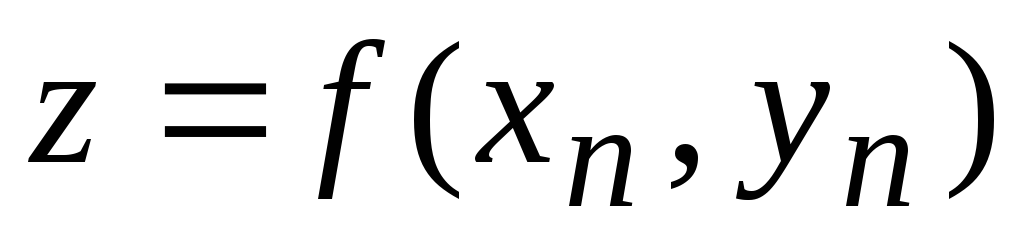

 и суммарная стоимость работ равна (6000 4- 8000 + 12 000) х 5 = 130 000 руб.
и суммарная стоимость работ равна (6000 4- 8000 + 12 000) х 5 = 130 000 руб.


 . Легко видеть, что линии уровня — это «веточки» гиперболы в 1-ми 3-м квадрантах. При увеличении с линии уровня отодвигаются от начала координат (рис. 2).
. Легко видеть, что линии уровня — это «веточки» гиперболы в 1-ми 3-м квадрантах. При увеличении с линии уровня отодвигаются от начала координат (рис. 2).







