Аналитический способ задачи последовательности

Способы задания числовой последовательности

Методические указания

Определение 1.Функцию y = f(x), x 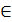N называют функцией натурального аргумента или числовой последовательностью и обозначают: y = f(n) или y₁, y₂, y₃, . y_n, . или (y_n).

В данном случае независимая переменная – натуральное число.

Способы задания числовой последовательности

Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.

Пример 1.Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . .

Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . .

Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, .

Любой n-й элемент последовательности можно определить с помощью формулы.

Пример 1. Последовательность чётных чисел: y = 2n.

Пример 2.Последовательность квадрата натуральных чисел: y = n 2 ;

1, 4, 9, 16, 25, . n 2 , . .

Пример 3. Стационарная последовательность: y = C; C, C, C, . C, .

Частный случай: y = 5; 5, 5, 5, . 5, . .

Пример 4. Последовательность y = 2 n ;

2, 2 2 , 2 3 , 2 4 , . 2 n , . .

Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы.

Пример 1. Арифметическая прогрессия: a₁=a, a_n+1=a_n+d, где a и d – заданные числа, d — разность арифметической прогрессии. Пусть a₁=5, d=0,7, тогда арифметическая прогрессия будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; . .

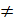
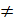
Пример 2. Геометрическая прогрессия: b₁= b, b_n+1= b_nq, где b и q – заданные числа, b 0, q 0; q – знаменатель геометрической прогрессии. Пусть b₁=23, q=½, тогда геометрическая прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; . .

Пример 3. Последовательность Фибоначчи. Эта последовательность легко задаётся рекуррентно: y₁=1, y₂=1,y_n-2+y_n-1, если n=3, 4, 5, 6, . . Она будет иметь вид: 1, 1,2, 3, 5, 8, 13, 21, 34, 55, . .

Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:

Пример 1. Составить возможную формулу n-го элемента последовательности (y_n):

а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2n+1.

б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой y = 4n.

Пример 2. Выписать первые десять элементов последовательности, заданной рекуррентно: y₁=1, y₂=2, y_n = y_n-2+y_n-1, если n = 3, 4, 5, 6, . .

Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.

Пример 3. Последовательность (y_n) задана рекуррентно: y₁=1, y₂=2,y_n=5y_n-1— 6y_n-2. Задать эту последовательность аналитически.

Найдём несколько первых элементов последовательности.

Получаем последовательность: 1; 2; 4; 8; 16; 32; 64; . которую можно представить в виде

2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 . .

n = 1; 2; 3; 4; 5; 6; 7. .

Анализируя последовательность, получаем следующую закономерность: y = 2 n -1 .

Источник

Урок по теме :Последовательности. Словесный и аналитический способы ее задания

Разработка урока по теме «Последовательности. Словесный и аналитический способы ее задания»

Создание условий для формирования понятия числовой последовательности и способов её задания;

развитие способности к обобщению, сравнению; эмоционального восприятия математических объектов;

формирование представлений о математике как способе познания, сохранения и гармоничного развития мира.

умение понимать смысл поставленной задачи, ясно и чётко излагать свои мысли в устной речи;

самооценка результатов деятельности, осознание границ применения нового знания;

умение работать в паре;

ценностно-эмоциональное отношение к изучаемому математическому содержанию с общекультурных позиций;

представление о значении математической науки как сфере человеческой деятельности.

умение выделять главное, сравнивать, обобщать, проводить аналогию, выдвигать гипотезы при решении учебных задач;

осознанное чтение текста;

представление о математике как средстве моделирования явлений окружающего мира.

понятие числовой последовательности;

умение использовать индексные обозначения и строить речевые высказывания с использованием специальной терминологии;

умение устанавливать закономерность в построении последовательности, если выписаны первые несколько её новых членов;

Сегодня мы приступаем к изучению новой для вас темы. Эта тема поможет открыть последовательности , встречающиеся в нашей жизни. Надеюсь, что сегодняшний урок, выводя вас на смыслы изучаемых понятий, поможет освоить новую тему с интересом и хорошими результатами.

2. Актуализация знаний учащихся (просмотр видеоролика на тему «Числа Фибоначчи»)

Вопросы по слайду. Числа Фибоначчи.

Что видим на слайде?

Как вы думаете почему именно так он записал числа?

А можно сказать, что это числовой ряд?

А какую закономерность он использовал при написании этого ряда чисел?

Попробуем догадаться. Как вы думаете? (каждое последующее число больше суммы двух предыдущих).

Что увидел Фибоначчи? (пример с листьями цветка).

Значит что он построил? ( числовой ряд или по другому можно сказать последовательность чисел)

3. Изучение нового материала

Чем же сегодня на уроке мы будем заниматься? Тема нашего урока — ПОСЛЕДОВАТЕЛЬНОСТИ.

-Запишем в тетрадь.

— Разбор опроса учащихся (вывешивание листочков с определением – последовательности.

Итак, некоторые из- вас ответили так, а в толковом словаре Даля так.

— Но, а в математике мы попробуем сейчас выяснить.

Задача. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день? ( ответ 500, 530,560,590,620,….)

Попробуйте по первым числам догадаться, по какому правилу построены эти числовые множества. ( Попробуйте найти следующее за ним число)

Проверка выполнения: устное представление результатов выполнения задания.

1) 1, 2, 3, 4, 5, 6, … — натуральные числа;

2) 2, 4, 6, 8,10, … — чётные числа;

3) 1, 3, 5, 7, 9, … — нечётные числа;

4) 1, 4, 9, 16, 25, 36, … — квадраты натуральных чисел:

5) 2, 3, 5, 7, 11, 13, 17, … — простые числа;

6) 1, , , , , ,…- числа, обратные натуральным .

По ходу обсуждения на слайде появляются следующие члены последовательностей и названия этих числовых множеств.

Задание Попробуйте определить, что является общим и главным для всех этих чисел.

Проверка выполнения: устное представление каждого из своих гипотез.

Предполагаемый ответ: Общим для всех рядов чисел является то, что числа записаны в определённом порядке, последовательности.

В ходе обсуждения должны появиться следующие слова: очерёдность, порядок и т.п.

(Работа с учебником)

У вас на столах листочки с пропусками слов. Сейчас с помощью учебника и своего соседа вы будете помогать друг другу заполнять листочки с пропущенными словами.

Попробуйте сформулировать определение понятия «числовая последовательность».

Проверка выполнения: каждая пара представляет свою формулировку определения.

Сравните своё определение с определением из школьного учебника: «Числовая последовательность – это записанные в определённом порядке числа».

В общем случае числовые последовательности могут быть конечными и составлены из произвольных чисел. Числовыми последовательностями, например, являются выписанные по порядку отметки каждого из вас в классном журнале по алгебре или результаты каких-либо измерений: например, температуры воздуха. Главным является именно порядок: каждое число стоит на своём месте. Запишем числовую последовательность в общем виде.

Все числа последовательности называются членами последовательности, индексы 1, 2, 3, … — номерами членов последовательности.

– Как записать член последовательности с номером 4?

– Какой номер будет у члена последовательности, предшествующего а_п?

– А у следующего за ним?

– Как записать член последовательности, предшествующий а_п?

– Следующий за ним?

-Способы задания последовательности. Примеры.

-Числовая последовательность считается заданной, если указан способ, позволяющий найти член последовательности любого номера.

Эти правила вы оставите себе и приклеите в тетради, памятка.

6. Закрепление нового материала.

-Давайте, теперь определим как наши открытия помогут выполнить задания №560, №564, №565 (а) №569 (а), 567.

Выпишите первые несколько членов последовательности натуральных чисел, кратных 3, взятых в порядке возрастания. Укажите ее первый, пятый, десятый, сотый и n -й члены.

Решение: 3; 6; 9; 12; … а₁ = 3, а₅ = 15, а₁₀ = 30, а₁₀₀ = 300, а _n = 3 n

Найдите первые шесть членов последовательности, заданной формулой n — го члена: х _n = 2 n – 1.

Решение: 1, 2, 3, 4, 5.

№567 (для сильных учащихся) Если осталось время

Последовательность а _n задана формулой а _n = n 2 — n -20. Определите номера отрицательных членов и вычислите их.

7. Тестовая проверочная работа

1.Последовательность задана формулой a _n =5 n +2 . Чему равен её третий член?

2 . Выпишите 5 первых членов последовательности, заданной формулой a _n = n -3

3. Найдите сумму 6-ти первых членов числовой последовательности: 2,4,6,8,

(Контрольно-измерительные материалы по математике ОГЭ ФИПИ И.В.Ященко . )

— Проверка (в парах). Выставление оценок.

Конечно же, русское слово последовательность было знакомо вам ещё до сегодняшнего урока. Посмотрите, какие синонимы существуют у этого слова:

— череда, вереница, цепочка;

Какой синоним наиболее отвечает вашему представлению о последовательностях?

С чем лично у вас ассоциируется понятие последовательности?

Что вам дало изучение понятия числовой последовательности?

Что вызвало наибольшие затруднения?

— Что узнали нового? (последовательности)

— Как можно задать числовые последовательности? (словесно, формулой n — го члена, рекуррентным способом)

— Какие бывают последовательности? (конечные, бесконечные)

— Где может пригодиться умение работать с последовательностями? (при дальнейшем изучении математики, при сдаче ОГЭ и в жизни, в природе)

Домашнее задание: п. 24, № 562, 565 (в, д), 573(а). Для желающих

5 б. – все понял и могу объяснить другому;
4 б. – сам понял, но объяснить не берусь;
3 б. – для полного понимания надо повторить;
2 б. – я ничего не понял.

Числовая последовательность – это записанные в определённом порядке ______________. Числа, образующие последовательность, называются _______________________
____________________. Члены последовательности обозначаются _____________ с ____________, указывающими ________________ номер члена. Член последовательности с номером n , называется ___________

_____________ последовательности, обозначают ______.

Последовательности, содержащие бесконечно много членов называются ______________. Последовательности, содержащие конечное число членов называются ________________. Способы задания последовательностей:

словесный ______________________________________, рекуррентный _____________________________________.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-745840

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

ЕСПЧ запретил учителям оскорблять учеников

Время чтения: 3 минуты

В Осетии студенты проведут уроки вместо учителей старше 60 лет

Время чтения: 1 минута

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

В МГУ разрабатывают школьные учебники с дополненной реальностью

Время чтения: 2 минуты

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник