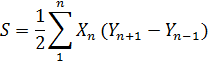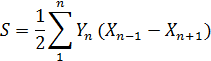- Основы геодезии
- О геодезии и разный полезный материал для геодезистов.
- Аналитический способ
- Вычисление площади участка по координатам вершин основного теодолитного хода
- Практическая работа на тему: Определение площади полигона по координатам его вершин.
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Аналитический способ
При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.
Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) – рис.6.2.
Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.
Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)
Выразим площадь каждой трапеции через ее основания и высоту:
Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:
или в общем виде:
В этой формуле индекс “i” показывает номер вершины треугольника; индекс “i” означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).
Если при группировке членов выносить за скобки Y1, то получится формула:
Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.
Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n – угольника.
Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n – угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.
Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.
На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.
Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:
Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой – сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,
Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:
Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:
mP=an * mt * L, (6.17)
где: L – периметр многоугольника,
an – коэффициент, зависящий от n – количества вершин; 
его значения:
n 3 4 5 6 7 8 9 10
an 0.204 0.250 0.256 0.250 0.243 0.231 0.222 0.212
n 11 12 15 20 24 30 60 120
an 0.205 0.197 0.179 0.156 0.143 0.128 0.091 0.065
Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n – угольника. Так, если площадь неправильного n – угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.
При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).
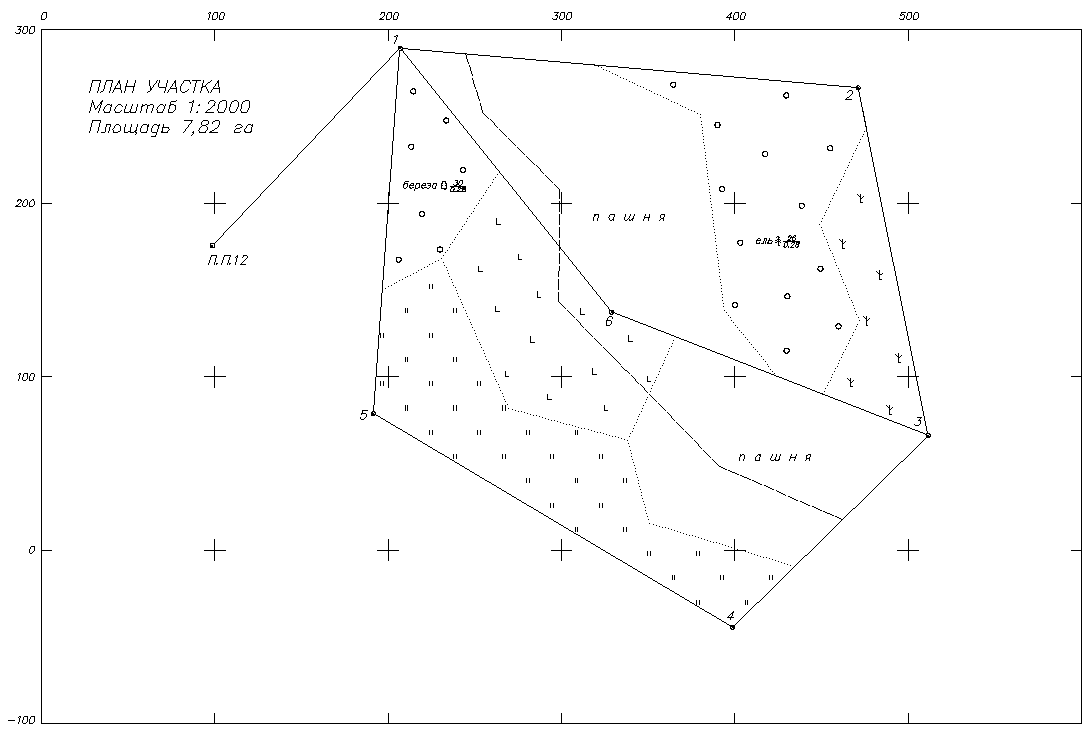
Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.
Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.
При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.
Площадь правильного n-угольника можно выразить через его периметр:
И из формулы (6.17) получить формулу относительной ошибки площади:
для треугольника (n=3) mp/P = 4.24* mt/L,
для четырехугольника (n=4) mp/P = 4.00* mt/L,
для пятиугольника (n=5) mp/P = 3.72 mt/L,
для шестиугольника (n=6) mp/P = 3.46 mt/L.
Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:
ошибка этой формулы может достигать 15% – 20% для участков, форма которых заметно отличается от формы правильного n -угольника.
Источник
Вычисление площади участка по координатам вершин основного теодолитного хода
Площадь замкнутого полигона по координатам его вершин определяют по формулам:
X,Y – координаты вершин основного теодолитного хода;
n – вершины хода;
(n+1) – номер последующей вершины;
(n – 1) – номер предыдущей вершины.
По обеим формулам должно получиться одно и то же значение площади, что является контролем вычисления площади участка.
Вычисляют площадь по приведенным формулам в специальной «Ведомости вычисления площади участка по координатам» (табл.6).
Вначале из «Ведомости вычисления координат основного замкнутого хода» (табл.4) переносят в «Ведомость вычисления площади» (табл.6) координаты вершин замкнутого полигона. После этого вычисляют разности соответствующих ординат (графы 2 и 3) и соответствующих абсцисс, указанных в приведенных формулах площади, число разностей равно числу вершин полигона.
В примере: 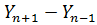
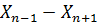
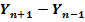 | 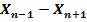 |
1. 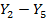 = 471,08 – 191,42 = 279,66 = 471,08 – 191,42 = 279,66 | 1 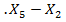 =78,54-266,54 = =78,54-266,54 = 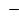 188,00 188,00 |
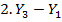 = 511,48 – 206,93 = 304,55 = 511,48 – 206,93 = 304,55 | 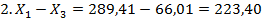 |
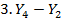 = 398.81 – 471,08= — 72,27 = 398.81 – 471,08= — 72,27 | 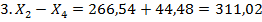 |
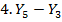 = 191,42 – 511,48 = -320,06 = 191,42 – 511,48 = -320,06 | 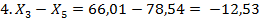 |
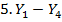 = 206,93 – 398,81 = — 191,88 = 206,93 – 398,81 = — 191,88 | 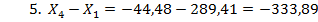 |
Алгебраическая сумма разностей абсцисс и ординат должна равняться нулю, что является контролем вычисления соответствующих разностей. Полученные разности абсцисс и ординат заносят в графы 6 и 7 ведомости. Произведения алгебраически суммируют отдельно в графе 6 и в графе 7. Суммы должны быть одинаковыми, что является контролем вычислений. Сумма произведений в графе 6 и в графе 7 составляют двойную площадь участка.
В примере: 2S= 156506, 62 м 2 , а площадь полигона
S = 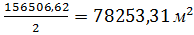
Все вычисления площади записывают в ведомость (табл. 6).
Ведомость вычисления площади участка по координатам
| № точек | Координаты | 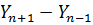 | 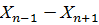 | 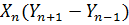 | 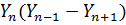 |
| Х | Y | ||||
| +289,4 | +206,93 | +279,66 | — 188,00 | +80936,40 | -38902,84 |
| +266,54 | +471,08 | +304,55 | + 223,40 | +81174,76 | +105239,27 |
| +66,01 | +511,48 | -72,27 | +311,02 | -4770,34 | +159080,50 |
| -44,48 | +398,81 | — 320,06 | -12,53 | +14236,26 | -4997,09 |
| +78,54 | +191,42 | -191.88 | -333,89 | -15070,26 | -63913,22 |
| +584,21 — 584,21 | +534,42 -534,42 | 156506,62 | 156506,62 | ||
| 2S=156506,62м 2 S = 78253,31м 2 |
На защиту необходимо представить:
1. Обработанный журнал теодолитной съемки.
2. Ведомость вычисления координат точек теодолитных ходов.
4. Ведомость вычисления площади участка.
5. Расчетно-графическая работа должна иметь титульный лист (рис.11).
1. Маслов А.В., Гордеев А.В., Батраков Ю.Г., Геодезия. — М.: КолосС 2006. — 599 с.
2. Поклад Г.Г., Гриднев С.П.Геодезия. — М.: Академический проект 2007. — 592 с.
Источник
Практическая работа на тему: Определение площади полигона по координатам его вершин.
ТЕМА : Определение площади полигона по координатам его вершин.
ЦЕЛЬ : Определить площадь полигона аналитическим методом.
1. Координаты вершин полигона
2. Направление измерения углов полигона (правые).
Полигоном называют территорию, ограниченную замкнутым теодолитным ходом. При известных координатах вершин теодолитного хода площадь полигона или любой фигуры ограниченной прямыми линиями можно вычислить по двум формулам:
Удвоенная площадь полигона равна сумме произведений абсциссы каждой точки на разность ординат последующей и предыдущей точек.
Она же (удвоенная площадь) равна сумме произведений каждой ординаты на разность абсцисс предыдущей и последующей точек.
СОДЕРЖАНИЕ И ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ:
1. В ведомость вычисления площади полигона в графу 1 занести номера вершин хода.
2. В графы 2, 3 занести координаты по осям х и у.
3. Графы 4, 5 вычислить по формулам:
4. Подбить суммы граф 4, 5, (Суммы должны равняться нулям).
5. Графы 6, 7 вычислить по формулам:
6. Найти среднее значение удвоенной площади полигона и определить площадь полигона в гектарах.
Таблица 1- Ведомость вычисления площади полигона по координатам его вершин .
Курс повышения квалификации
Охрана труда
- Сейчас обучается 93 человека из 44 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 336 человек из 66 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 171 человек из 48 регионов
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-165606
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Шойгу предложил включить географию в число вступительных экзаменов в вузы
Время чтения: 1 минута
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Минпросвещения работает над единым подходом к профилактике девиантного поведения детей
Время чтения: 1 минута
В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник