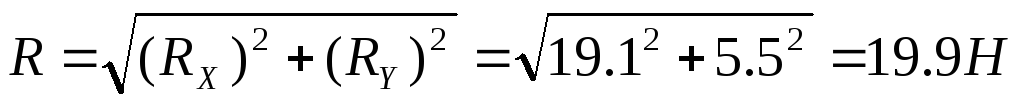Аналитический способ сложения векторов

Содержание

Аналитический способ сложения сил
Равновесие системы сходящихся сил
Системы статически определимые и статически неопределимые
Решение задач статики

Аналитический способ сложения сил

Теорема: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

ЕслиR = F₁ + F₂ + F₃ + … + F_n, причем (F₁_x, F₁_y, F₁_z), (F₂_x, F₂_y, F₂_z), …, (F₃_x, F₃_y, F₃_z) – наборы проекций этих векторов на оси X, Y и Z то

Модуль результирующей силы:

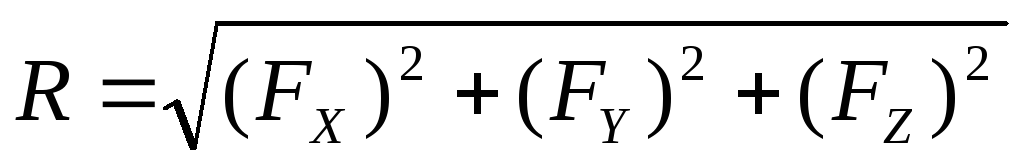
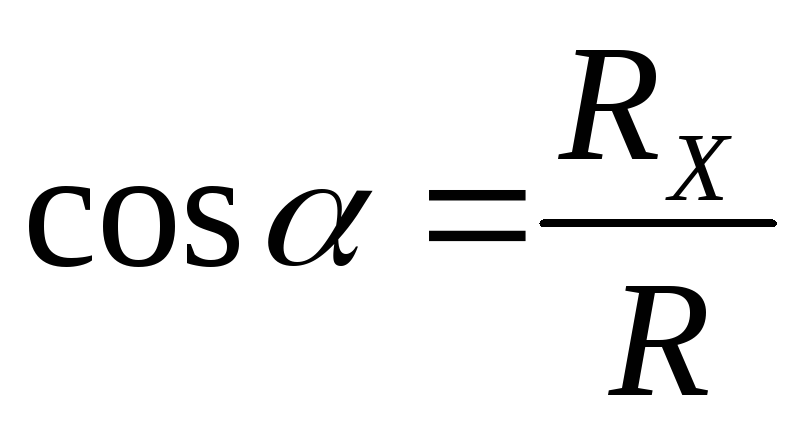
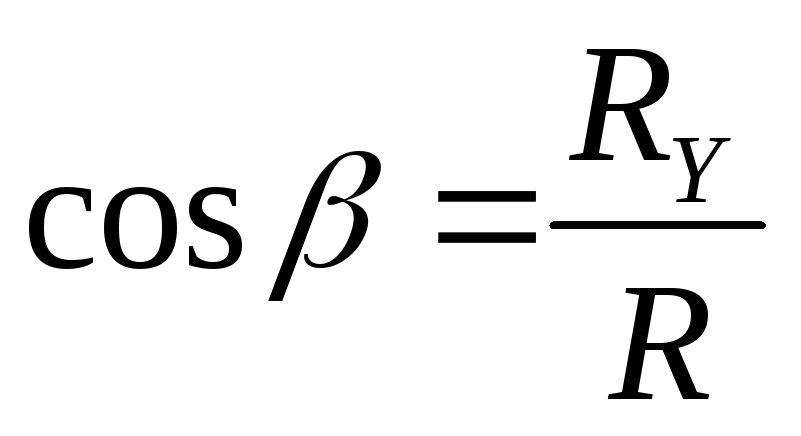
Направление результирующего вектораR определяется направляющими косинусами:

; ; .

Пример 1. Определить результирующую силу трех силF₁, F₂, F₃ проекции которых заданы: F₁(3;3), F₂(6;-2), F₃(-5;-3). Силы заданы в Ньютонах (рис. 2.4).

Решение:

R_x = 3 + 6 – 5 = 4H; R_y = 3 – 2 – 3 = -2H;

одуль результирующей силы:

Ответ: R = 4,5H;  = 63 o ;  = 27 o .

Пример 2. Задана плоская система сил, действующая на точку А. F₁ = 15Н; F₂ = 10Н. Определить равнодействующую силу (рис. 2.5).

Р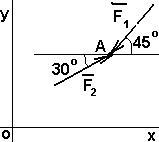ешение:

Определим сумму проекций данных сил на оси OX и OY:

Ось OX:

сьOY:

Подставляя численные значения получим:

Модуль равнодействующей:

Направляющие косинусы: ; .

Ответ: R = 19,9H;  = 74 o ;  = 16 o .

Равновесие системы сходящихся сил

Система сходящихся сил – это силы, сходящиеся в одной точке (рис. 2.6).

Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.

налитические условия равновесия. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

Теорема о трех силах. Если свободное твердое тело находится в состоянии равновесия под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

F₁ + F₂ + F₃ = 0

Системы статически определимые и статически неопределимые

Задача статики может быть решена лишь в том случае, когда для нее число неизвестных реакций связей не превышает число уравнений равновесия, содержащих эти реакции. Такие задачи называют статически определенные, а система тел, для которых это имеет место – статически определимыми системами.

Задачи, в которых число неизвестных реакций связей больше числа уравнений равновесия, содержащих эти реакции, называются статически неопределенные, а система тел для которых это имеет место – статически неопределимыми системами.

римером для статически неопределенной системы может служить груз, подвешенный на трех нитях, лежащих в одной плоскости (рис. 2.7). В этой задаче три неизвестные силы натяжения нитиT₁, T₂, T₃, а уравнений равновесия в случае плоской системы сходящихся сил можно составить только два.

Решение задач статики

Для решения задач статики необходимо:

Выбрать тело, равновесие которого должно быть рассмотрено.

Освобождение тела от связей и изображение действующих на него заданных сил и реакций отброшенных связей.

Составление уравнений равновесия.

Определение искомых величин, проверка правильности решения и исследование полученных результатов.

Для решения задач на равновесие тела под действием сходящихся сил можно использовать следующие способы:

а) Геометрический способ. Применяется если число сил, действующих на тело равно трем. При равновесии треугольник, построенный на этих силах, должен быть замкнутым.

б) Аналитический способ. Применяется при любом количестве сил, действующих на тело. В случае плоской системы сходящихся сил составляется два уравнения равновесия, а в случае пространственной системы сил – три.

Пример №3. К вертикальной гладкой стене АВ подвешен на тросе АС однородный шар. Трос составляет со стеной угол, сила тяжести шара Р. Определить силу натяжения троса Т и давление шара на стену Q. Шар находится в равновесии под действием этих трех сил (рис. 2.8а).

Рассмотрим решение задачи геометрическим (графическим) способом. Так как шар находится в равновесии под действием трех сил, то эти силы сходящиеся. Точка, в которой сходятся эти силы, является геометрическим центром шара (точка О). Построим силовой треугольник (рис. 2.8б). Построение начинают с известной силы Р.

Силовой треугольник должен быть замкнут. В данном случае это прямоугольный треугольник. Тогда: ;

твет:; .

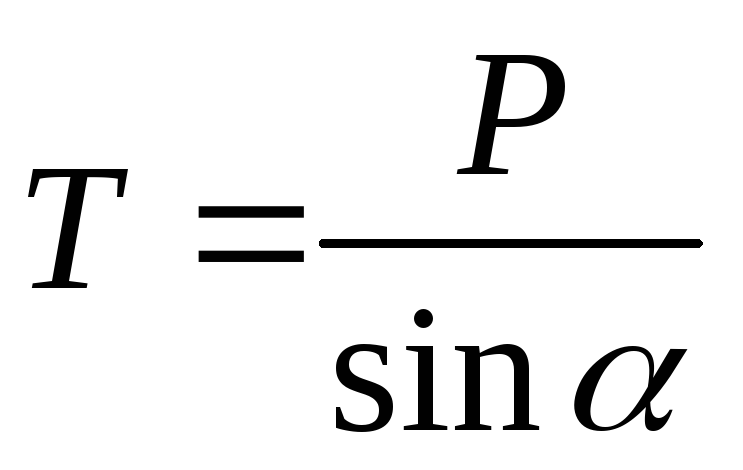
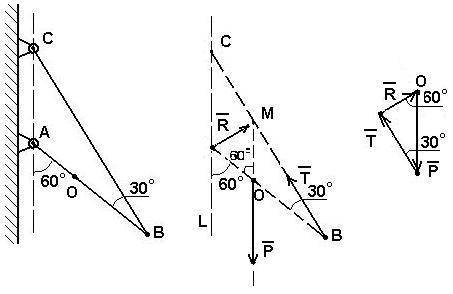
ример №4. Однородный стержень АВ прикреплен к стенке посредством шарнира А и удерживается под углом 60 0 к вертикали при помощи троса ВС, образующего с ним угол 30 0 (рис. 2.9а). Определить величину и направление реакции R шарнира, если известно, что вес стержня равен 20Н.

Определим силы, действующие на данную конструкцию:

Р – сила тяжести стержня АВ, так как стержень однородный, то сила приложена к его геометрическому центру (точка О).

Т – натяжение троса СВ, направлено вдоль СВ.

R – реакция в шарнире А (направление неизвестно) (рис. 2.9б).

Согласно принципу освобождаемости от связей, заменим связи соответствующими реакциями.

Так как система находится в равновесии под действием трех сил, то эти силы должны сходиться, а поэтому сила реакции R направлена от А к М (точка пересечения сил Р и Т).

Построим силовой треугольник. Для этого выберем произвольную точку О и отложим от нее известную силу Р, сохраняя ее направление. Из конца вектора Р под углом 30 0 проведем луч, который соответствует направлению силы Т (рис. 2.9в).

Так как — 60 0 = 120 0 , тогда 0 – (120 0 + 30 0 ) = 30 0 , т.е. треугольник ОМВ равнобедренный: сторона ОМ = ОВ. Поэтому ОМ = ОВ = ОА, так как О является серединой АВ, а угол 0 , то треугольник АОМ является равносторонним. Поэтому 0 = 0 к направлению силы Р до пересечения с направлением силы Т. Полученный треугольник прямоугольный, поэтому R = Psin30 0 = 20/2 = 10H.

Пример №5. Три груза А, В и С массой 10, 20, и 60 кг соответственно лежат на плоскости, наклоненной под углом  к горизонту (рис. 2.10). Грузы соединены тросами, как показано на рисунке. Коэффициенты трения между грузами и плоскостью равны _А = 0,1, _В = 0,25, _С = 0,5 соответственно.

Определить угол , при котором тела равномерно движутся вниз по плоскости. Найти также натяжение тросов Т_АВ и Т_ВС.

Решение:

ассмотрим, какие силы действуют на каждое тело и запишем условие равновесия, так как тела движутся равномерно, то

сумма всех сил, действующих на тело равна нулю. На тело А действует сила тяжести Р_А, сила реакции опоры N_А, сила трения F_трА и сила натяжения троса Т_АВ (рис. 2.10б). Условие равновесия: Р_А + N_А + F_трА + Т_АВ = 0.

Выберем систему координат и спроектируем силы на оси:

Подставляя численные значения получим: 10sin — cos — Т_АВ = 0.

Рассмотрим, какие силы действуют на тело В: Р_В — сила тяжести, F_трВ — сила трения, Т_ВА— сила натяжения троса со стороны груза А, Т_ВС — сила натяжения троса со стороны груза С, N_В — сила реакции опоры (рис. 2.10в). Тогда условие равновесия будет: Р_В + N_В + F_трВ + Т_ВА + Т_ВС = 0.

Проектируя это уравнение на ось ОХ, получим:

На тело С действуют следующие силы: Р_С — сила тяжести, F_трС — сила трения, Т_СВ— сила натяжения троса со стороны груза В, N_С — сила реакции опоры (рис. 2.10г). Тогда условие равновесия при проектировании на ось ОХ будет: